手写算法-python代码实现非线性逻辑回归（带L1、L2正则项）

非线性逻辑回归分析

上一篇文章，我们介绍了逻辑回归，详情请看这里：

链接: 手写算法-python代码实现逻辑回归（带L1、L2正则项）

其实这是线性逻辑回归，决策边界是线性的，那么当一个数据集，它的划分边界是非线性时，我们该怎么处理？

我们利用sklearn来生成相关数据集：

import numpy as np
import matplotlib.pyplot as plt
#生成高斯分布数据
from sklearn.datasets import make_gaussian_quantiles

#生成2个特征、2个类别的的数据集
x,y = make_gaussian_quantiles(n_samples=200, n_features=2,n_classes=2,random_state = 2020)
#颜色=类别，这样画图很方便
plt.scatter(x[:,0], x[:,1], c=y) 
plt.show()

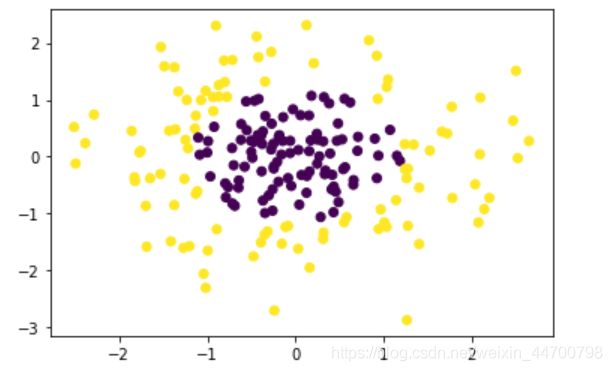
如图，此时当我们继续用普通逻辑回归去做分类时，可预估到，效果将会很差（前面我们讲非线性回归时，分析过，这里更适合x的多项式作为输入），想了解的请看这里：
链接: 手写算法-Python代码实现非线性回归

用python代码写的逻辑回归类画决策边界 & 用sklearn里面的逻辑回归库画决策边界

用我们写好的逻辑回归代码，看一看，不对x进行处理时，拟合分类边界还会是一条直线吗？

class LogisticRegression:
    
    #默认没有正则化，正则项参数默认为1，学习率默认为0.001，迭代次数为10001次
    def __init__(self,penalty = None,Lambda = 1,a = 0.001,epochs = 10001):
        self.W = None
        self.penalty = penalty
        self.Lambda = Lambda
        self.a = a
        self.epochs =epochs
        self.sigmoid = lambda x:1/(1 + np.exp(-x))
        
    def loss(self,x,y):
        m=x.shape[0]
        y_pred = self.sigmoid(x * self.W)
        return (-1/m) * np.sum((np.multiply(y, np.log(y_pred)) + np.multiply((1-y),np.log(1-y_pred))))
    
    def fit(self,x,y):
        lossList = []
        #计算总数据量
        m = x.shape[0]
        #给x添加偏置项
        X = np.concatenate((np.ones((m,1)),x),axis = 1)
        #计算总特征数
        n = X.shape[1]
        #初始化W的值,要变成矩阵形式
        self.W = np.mat(np.ones((n,1)))
        #X转为矩阵形式
        xMat = np.mat(X)
        #y转为矩阵形式，这步非常重要,且要是m x 1的维度格式
        yMat = np.mat(y.reshape(-1,1))
        #循环epochs次
        for i in range(self.epochs):
            #预测值
            h = self.sigmoid(xMat * self.W)
            gradient = xMat.T * (h - yMat)/m
            
            
            #加入l1和l2正则项，和之前的线性回归正则化一样
            if self.penalty == 'l2':
                gradient = gradient + self.Lambda * self.W
            elif self.penalty == 'l1':
                gradient = gradient + self.Lambda * np.sign(self.W)
          
            self.W = self.W-self.a * gradient
            if i % 50 == 0:
                lossList.append(self.loss(xMat,yMat))
        #返回系数
        return self.W


lr = LogisticRegression(epochs=50000)
w = lr.fit(x,y)

#前面讲过，z=0是线性分类临界线
# w[0]+ x*w[1] + y* w[2]=0,求解y (x,y其实就是x1,x2)
x_test = [[-3],[3]]
y_test = (-w[0]-x_test*w[1])/w[2] 

#画决策边界
plt.scatter(x[:,0],x[:,1],c=y)
plt.plot(x_test,y_test)
plt.show()

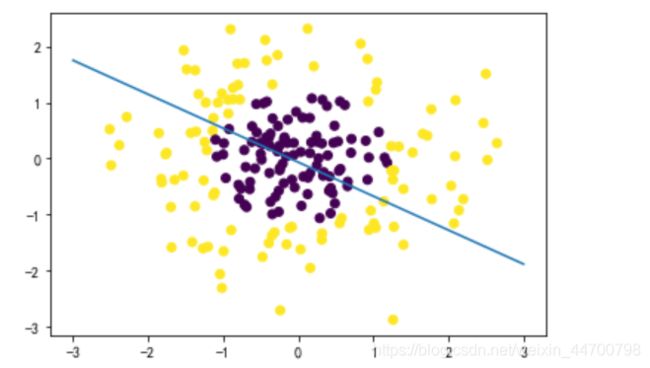
这个分类，好吧，对错各一半！接下来看看sklearn分类是什么样子：

from sklearn.linear_model import LogisticRegression as LR
clf =LR()
clf.fit(x,y)

plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

y_test_1 = (-clf.intercept_ - clf.coef_[0][0] * np.array(x_test))/clf.coef_[0][1]

fig =plt.figure()
ax1= fig.add_subplot()
ax1.scatter(x[:,0],x[:,1],c=y,label='样本分布')
ax1.plot(x_test,y_test,c='r',label='python代码拟合')
ax1.plot(x_test,y_test_1,c='k',label='sklearn拟合')
ax1.legend(prop = {'size':10}) #此参数改变标签字号的大小
plt.show()

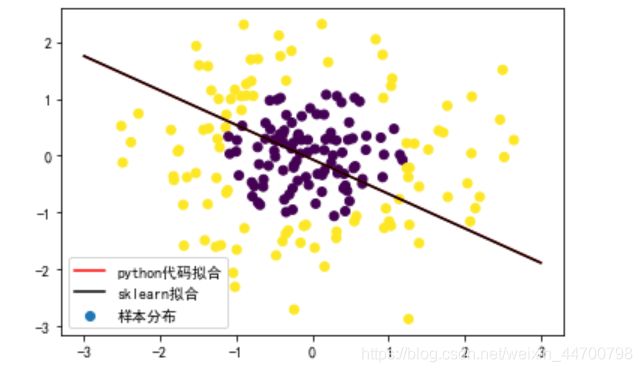
可以看到，两条线完全重合，直接调用sklearn里面的逻辑回归，结果也是一样。

多项式逻辑回归代码展示 & sklearn展示

我们需要对x进行处理，生成多项式，当最终的假设函数是这样的时候：

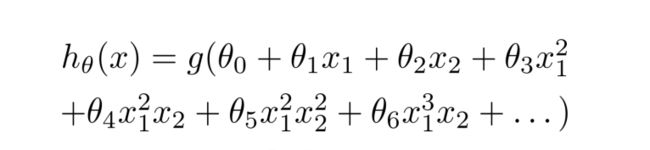
也许可以拟合得比较好。

实现代码：

#2个特征的x生成多项式函数
def multi_feature(x,n):
    c = np.empty((x.shape[0],0)) #np.empty((3,1))并不会生成一个3行1列的空数组,np.empty((3,0))才会生成3行1列空数组
    for i in range(n+1):
        for m in range(i,-1,-1):
            h=(x[:,0]**m) * (x[:,1]**(i-m))
            c=np.c_[c,h]
    return c


#对x进行多项式处理，生成新的x_1
#n这个值可以调，越大代表多项式越复杂，大家可以自己调整
x_1 = multi_feature(x,3)

#前面我们知道x_1已经生成了一列1的偏置，而函数里面会再次生成一列1的偏置，会重复，因此这里不要这生成的一列1
x_1 = x_1[:,1:]

lr = LogisticRegression(epochs=50000)
w = lr.fit(x_1,y)
print(w)

这个时候，x_1的形式比较复杂，之前的画图方式已经不合适了(注意：这个图的x,y都是特征列，y不是预测值)，我们画图换一个画法，画等高线图：

# 获取数据值所在的范围
x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1

# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))



#把xx,yy组成2维数据集
x_new = np.c_[xx.ravel(), yy.ravel()]

#对x_new展开多项式，此处就不用删除偏置1，因为不用把这个数据集放入代码中跑
x_new_1 = multi_feature(x_new,3)

#生成x_new_1的预测值，数组 * 矩阵 ，结果还是矩阵乘法，得到预测值
y_new_1 = lr.sigmoid(x_new_1 * w)

for i in range(len(y_new_1)):
    if y_new_1[i] > 0.5:
        y_new_1[i] = 1
    else:
        y_new_1[i] = 0
y_new_1 = y_new_1.reshape(xx.shape)

# 等高线图
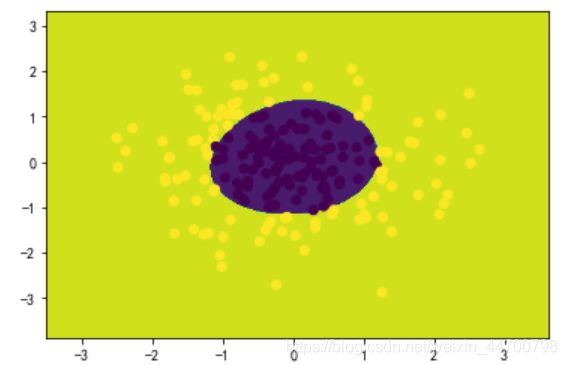
cs = plt.contourf(xx, yy, y_new_1)
plt.scatter(x[:,0],x[:,1],c=y)
plt.show()

可以看到，这个分类效果很完美！
调用sklearn的逻辑回归来看效果：

x_1 = multi_feature(x,3)
clf =LR()
clf.fit(x_1,y)

y_pred = clf.predict(x_new_1)  #直接输出类别
# 等高线图
cs = plt.contourf(xx, yy, y_pred.reshape(xx.shape))
plt.scatter(x[:,0],x[:,1],c=y)
plt.show()

结果也一样。

总结

这篇文章，首先是等高图，就适合画多特征的分类图；然后就是告诉我们不能拿到数据直接调用库，要了解底层数据，才可以做好机器学习。

逻辑回归和线性回归，是基础的机器学习，完全弄懂很有裨益，我们花了很多篇幅，来写这个系列，也是这个原因，基础打牢，多动手，多思考！