深度强化学习笔记(二)——Q-learning学习与二维寻路demo实现

深度强化学习笔记(二)——Q-learning学习与二维寻路demo实现

前言

这几天稍微闲下来，把原来漏的坑给补上，并做了一个Q-Learning的demo，因为Q-leraning的demo,目前我看到比较多的都是莫烦大佬讲的那个一纬寻路的demo，我觉得看起来没有那么有代表性，于是在此基础上，自己修改做了一个二维寻路的demo,奥利给

理论

什么是Q-Learning

Q-learning是一种无模式RL的形式，它也可以被视为异步DP的方法。它通过体验行动的后果，使智能体能够在马尔可夫域中学习以最优方式行动，而无须构建域的映射。智能体在特定状态下尝试行动，并根据其收到的即时奖励或触发以及对其所处状态的值得估计来评估其后果。 通过反复尝试所有状态的所有行动，它可以通过长期折扣奖励来判断总体上最好的行为。

算法

从状态$\Delta t$步进入未来步长的权重计算为${\gamma }^{\Delta t}$,$\gamma$(折扣因子)是介于0和1，并且具有对较迟收到的奖励(反映出良好开端的价值)进行估值的效果。$\gamma$也可以被解释为在每一步$\Delta t$都成功的概率
$$Q:S\times A->R$$
首先把Q-learning状态表的动作表初始化为0，然后通过训练更新每个单元。在每个时间t智能体选择动作$a_t$,观察奖励$r_t$,进入新状态$s_{t+1}$（可能取决于先前状态$s_t$和所选的动作),并对Q进行更新 ,该算法的核心是一个简单的值迭代更新过程,即使用旧值和新信息的加权平均值
$$Q^{new}(s_t,a_t)<-(1-\alpha )Q(s_t,a_t)+\alpha (r_t+\gamma ma{x}_{a}Q(s_{t+1},a))$$
其中,$r_t$是从状态$s_t$移动到状态$s_{t+1}$时收到的奖励,$\alpha$是学习率，$Q(s_t,q_t)$为旧值，$ma{x}_{a}Q(s_{t+1}m,a)$为信息

学习率

$\alpha$确定了新获取的信息在多大程度上覆盖旧信息。因子0使得智能体什么都不学习(专门利用先验知识),而因子1使得智能体只考虑最新信息(忽略先验知识，以探索可能性),一般情况下，通常使用恒定的学习率,${\alpha }_t=0.1$

折扣因子

折扣因子\gamma$决定了未来奖励的重要性。因子0将通过仅考虑当前奖励使得智能体近视，而接近1的因子将智能体努力获得长期高奖励。这种情况下，从较低的折扣因子开始并将其增加到最终值会加速学习

初始条件

由于Q-learning是迭代算法嘛,因此它隐含地假定在第一次更新发生之前的初始条件。高初始值,也称为"乐观初始条件",也可以鼓励探索:无论选择何种动作，更新规则将其使具有比其他替代方案更低的值，从而增加其选择概率

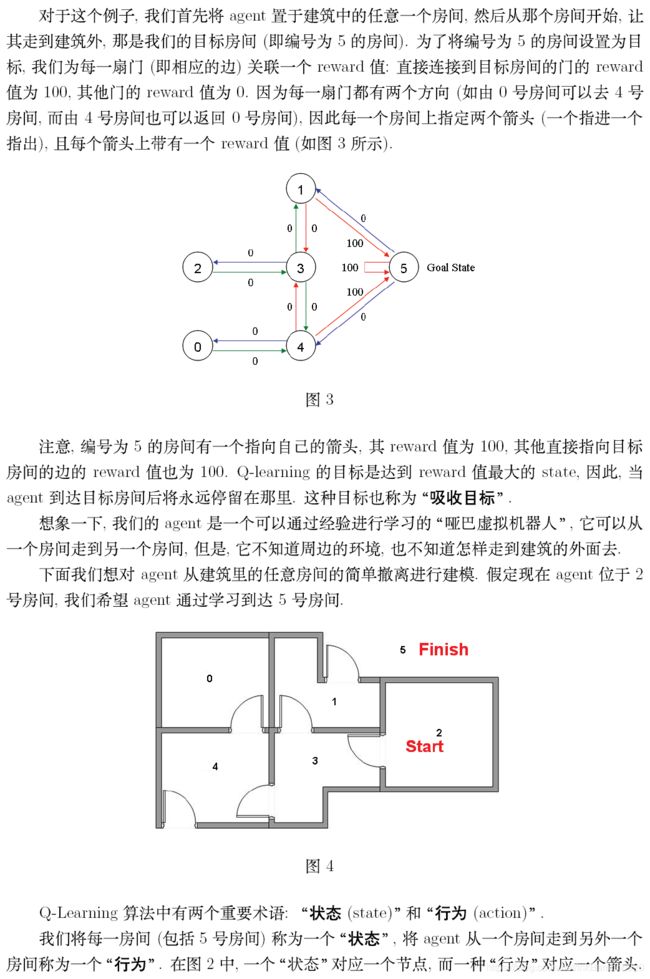
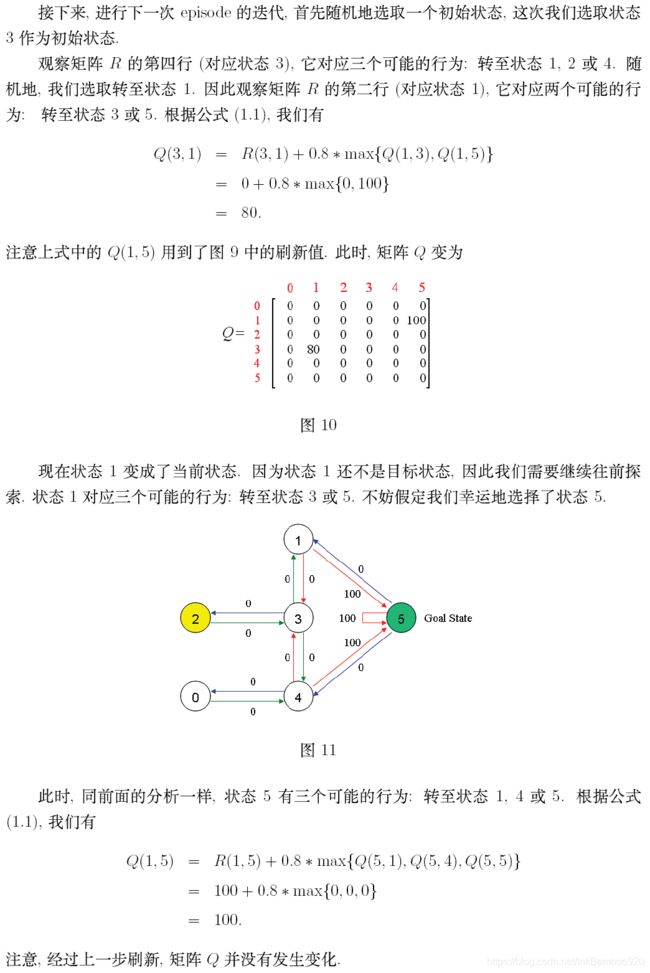
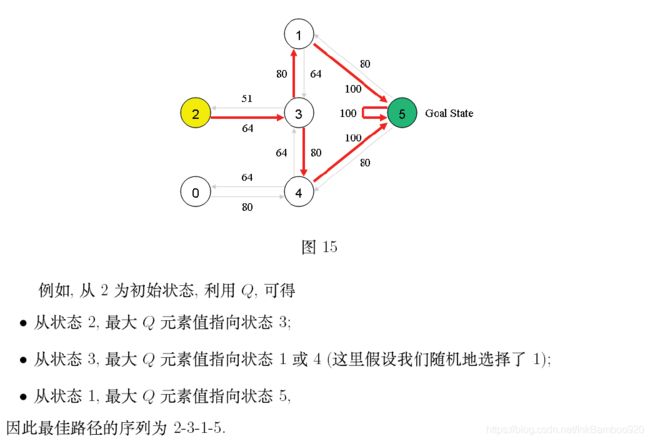
例子

原文链接:点我
翻译复制的一个大佬的作品:A Painless Q-learning Tutorial (一个 Q-learning 算法的简明教程)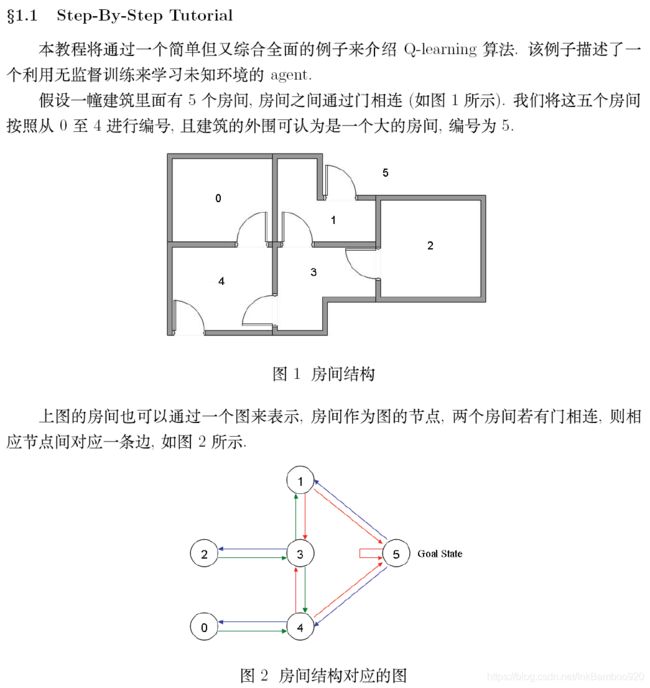

代码

因为有比较详细的注释，这里就不过多解释了

这里的代码最好在CMD里运行，由于jupyter notebook或者pycharm等IDE无法使用os.system('cls')清楚输出，会导致每次迷宫行动都是单独的一个，而不会在原基础更新，看起来比较难受~
升级版作图，由于IDE也不会更新，只会生成新的图，pycharm会存在生成25张图之后，就不会再生成了，无法看到后续变化,jupyter notebook会生成多张图，但是不容易看
如果有大佬知道解决方案，请私信或者评论里提出，谢谢大佬们

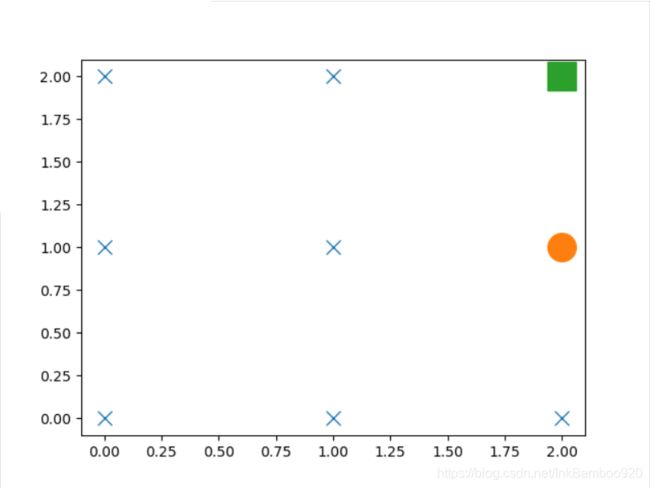
基础版走迷宫示意图

升级版走迷宫示意图

因为我暂时没有想到好的解决方法，大佬们可以自己想下，由于画图会增加内存，而当地图尺寸在5以上的时候，有部分由于随机种子的原因，在还前期训练的时候，有一两次的训练的轮数达到400次左右，导致内存占用过高，而训练图崩溃，大佬们可以想下怎么解决

完整代码

import numpy as np
import pandas as pd
import time
from matplotlib import pyplot as plt
import os

np.random.seed(3) #固定随机种子，方便调试
N_STATES = 3#迷宫的边长
ACTIONS = ['up','down','left', 'right']#动作,上下左右移动
EPSILON = 0.9#随机率,每10次，选择一次新的随机动作
ALPHA = 0.1#学习率
GAMMA = 0.9#折扣率，当折扣率为0时，则只关注当前奖励，而接近1则关注长期奖励
MAX_EPISODES = 20#最大EPISODERS次数
FRESH_TIME = 0.1#移动时间
X=1#初始坐标x
Y=1#初始坐标Y
target_x=3 #宝藏坐标x
target_y=3 #宝藏坐标y
NOW_STATE=0 #当前位置对应的Q表值

#生成初始Q表
#因为边长为N，每个点有上下左右四个选择，则数量为N*N*4
#N:N
#ACTIONS:动作
def build_q_table(N, actions):
    table = pd.DataFrame(
        np.zeros((N*N, len(actions))),
        columns=actions,
    )
    #(table)
    return table

#选择动作
#EPSILON:选择新动作的概率为1-EPSILON
#state:当前的状态位置(已经转换为一维表上的值)
#q_table:Q表
def choose_action(state, q_table):
    state_actions = q_table.iloc[state, :]
    if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()):
        #当前可以选择的动作表得奖励值都为0(即初始表)时，或者当随机数大于EPSILON时，随机选择一个新动作
        action_name = np.random.choice(ACTIONS)
    else:
        #否则选则当前可选动作表里奖励最大的值
        action_name = state_actions.idxmax()
    #返回要选择的动作的名字
    return action_name

#更新当前位置
def get_env_feedback(x,y,A):
    if A == 'up':  #向上移动
        #达到上边界，不做变化
        if y==1:
            y=y
        else:
            y=y-1
    elif A=='down':
        #到达下边界，不做变化
        if y==N_STATES:
            y=y
        else:
            y=y+1
    elif A=='left':
        #到达左边界，不做变化
        if x==1:
            x=x
        else:
            x=x-1
    elif A=='right':
        #到达右边界，不做变化
        if x==N_STATES:
            x=x
        else:
            x=x+1
    R=0
    # 判断是否达到终点，到达则将奖励置于1
    if (x == target_x) and (y==target_y):
        R=1
    return x,y,R

# 若到达宝藏位置，则打印本回合的序号和经历的步数。
# 否则打印本次移动后小人的位置（二维世界的当前状态）
def update_env(x,y,target_x, target_y, episode, step_counter):
    #做一个以+为点的坐标,*为宝藏
    env_list = np.array(['+']*(N_STATES*N_STATES))
    env_list=env_list.reshape(N_STATES,N_STATES)
    #确定是否达到终点
    if (x == target_x) and (y==target_y):
        interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter)
        print(interaction+'\n', end='')
        time.sleep(2)
        step_counter=0
        return step_counter
    else:
    #若未达到终点
        #老版本0.01显示图像
        env_list[target_x-1][target_y-1]='*'
        env_list[x-1][y-1] = 'o'
        interaction=''
        for a in range(N_STATES):
            interaction1 = ''.join(env_list[a,:])
            interaction1=interaction1+'\n'
            interaction=interaction+interaction1
        print(interaction)
        time.sleep(0.3)
        os.system('cls')
        #升级版迷宫图
        # label_x=np.array(range(N_STATES))
        # label_y=np.array(range(N_STATES))
        # label_x = label_x.reshape(N_STATES, 1)
        # label_x = np.tile(label_x, (1, N_STATES))
        # label_x = label_x.reshape(N_STATES*N_STATES)
        # label_y = np.tile(label_y, (N_STATES, 1))
        # label_y = label_y.reshape(N_STATES*N_STATES)
        # plt.ion()
        # plt.cla()
        # plt.plot(label_x, label_y, 'x', markersize=10)
        # plt.plot(x-1, y-1, 'o', markersize=20)
        # plt.plot(target_x-1, target_y-1, 's', markersize=20)
        # plt.show()
        # plt.pause(0.01)
        return step_counter-1

# 强化学习主要的控制器
#step_counter:记录该次episode运行了多少次
#is_terminated:是否是终点
def rl(X_1,Y_1,target_x,target_y):
    #c创建初始化零值表
    q_table = build_q_table(N_STATES, ACTIONS)
    #循环最大次数
    step_counter = 0
    for episode in range(MAX_EPISODES):
        X=X_1
        Y=Y_1
        is_terminated = False
        step_counter=update_env(X,Y,target_x,target_y,episode, step_counter)
        #如果不是终点，则进行循环
        while not is_terminated:
            #当前状态为第x列第y行对应的值
            NOW_STATE=int((Y*EPSILON-1)+X-1)
            A = choose_action(NOW_STATE, q_table)
            #更新当前位置,进行行为并获取奖励和下一次的状态
            X_,Y_,R = get_env_feedback(X,Y, A)
            q_predict = q_table.loc[NOW_STATE, A]
            #确定是否达到终点
            if (X_ != target_x) or (Y_!=target_y):
                NOW_STATE_ = int((Y_ * EPSILON-1) + X_-1)
                q_target = R + GAMMA * q_table.iloc[NOW_STATE_, :].max()
            else:
                q_target = R
                is_terminated = True
            #更新Q表
            q_table.loc[NOW_STATE, A] += ALPHA * (q_target - q_predict)
            #移动到下一个状态
            X=X_
            Y=Y_
            #打印状态
            step_counter=update_env(X,Y,target_x,target_y, episode, step_counter+1)
            step_counter += 1
    return q_table
if __name__ == "__main__":
    q_table = rl(X,Y,target_x,target_y)
    print('\r\nQ-table:\n')
    print(q_table)