莫烦Python代码实践（一）——Q-Learning算法工程化解析

提示：转载请注明出处，若本文无意侵犯到您的合法权益，请及时与作者联系。

莫烦Python代码实践（一）——Q-Learning算法工程化解析

声明

一、Q-Learning算法是什么？

二、Q-Learning算法的工程化

1、 随机初始化每一个状态s处的每一个动作a的价值

2、构建遍历每个episode和遍历每个step的循环

3、按照某种策略选择观测值observation下的动作action

4、进行Q表中价值的学习更新

 

---

---

声明

本文是作者学习莫烦Python的代码笔记总结，如想深入可移步莫烦Python的该课程。本文只讨论Agent角度的代码实现。

---

一、Q-Learning算法是什么？

Q-Learning的算法流程如下：

二、Q-Learning算法的工程化

下面考虑使用代码进行工程化：

1、 随机初始化每一个状态s处的每一个动作a的价值

在Q-Learning算法中就是用一个行数为所有状态数，列数为所有动作数的二维表（这里称为Q表）来存储，在Python中我们可以使用pandas库的数据结构——二维表DataFrame来初始化这个数据结构：

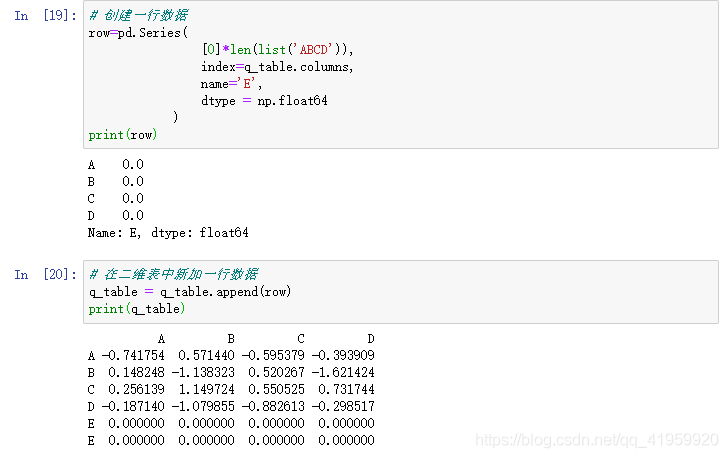
在上述代码中我们创建了一个固定行列数的内容随机的二维表。但是在应用时，我们的二维表的行数是要动态变化的，即当访问到了某个状态时我们再把它加到二维表格里，没有访问到该表格就先不添加，理论上这些状态我们都会访问到，这里进行这样的处理是一种提高效率的编程技巧，所以我们继续看一下如何在上述的二维表中添加一行新数据：

上图中使用到了pandas库中的另一个数据结构Series，关于Pandas的用法，可以查看我的博客。

现在，我们来设计一套可以自定义列名、行数据可以随时添加的二维表的解决方案：

# 创建一个动作数为4的列表
actions=list(range(4))
# 创建一个列名为actions的存储数据类型为float64的二维表格
q_table = pd.DataFrame(columns=actions,dtype = np.float64)

def check_state_exist(state):
    """检查该状态是否存在，不存在则添加"""
    global q_table
    if state not in q_table.index:
        # 添加新的一行数据到Q表中
        q_table =q_table.append(
            pd.Series(
                [0]*len(actions),
                index=q_table.columns,
                name=state,
            )
        )

注意上述有使用到global这个关键字，这是为了在函数中声明q_table为全局变量。

现在我们向其中动态添加一个状态名为‘a’的数据：

可以看到我们已经成功得到了一套可以自定义列名、行数据可以随时添加的二维表的解决方案。

我们将用这套解决方案来初始化我们的Q表。

2、构建遍历每个episode和遍历每个step的循环

# 遍历每一个episode    
for episode in range(100):
    # 初始化初始观测值
    observation = env.reset()
    # 遍历每一个step
    while True:
            ...

            # 当该回合结束时结束回合
            if done:
                break

在上述这个双重循环中，我们使用了env的必备接口reset()来初始化我们的初始状态的观测值observation。

外层循环的终止条件为达到设定的episode数，这里我们默认为常量，实际可以设置成为一个变量。

内层循环的终止条件为满足episode终止条件，这个一般通过检查env在每个step中返回的标志变量来实现。

3、按照某种策略选择观测值observation下的动作action

这里我们使用的是 Epsilon greedy （）的策略，即epsilon = 0.9 时, 就说明有90% 的情况Agent会按照 Q 表的最优值选择行为, 10% 的时间使用随机策略选择行为。

我们现在的需求是输入一个observation，按照Epsilon greedy选择observation对应的一行数据中的某个动作价值最高的动作或者是其随机的一个动作。

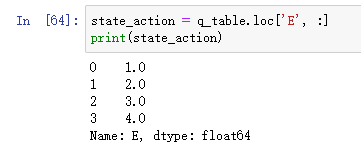
首先我们需要拿到observation对应的二维表中的行数据state_action，方法如下：

现在我们要访问行数据中价值最大的索引：

现在我们可以得到如何通过代码来实现 Epsilon greedy策略：

def choose_action(observation,epsilon=0.1):
        """根据当前Q-Table中状态的观测值来获取应当采取的动作"""
        global q_table
        check_state_exist(observation)
        # 采用ϵ−greedy策略来选择动作
        if np.random.rand() < epsilon:
            # 获取Q-Table中行名字为observation的包含全部列的一行数据
            state_action = q_table.loc[observation, :]
            # 获取这一行数据中价值最大的动作，如果存在多个则随机选择其中一个
            action = np.random.choice(state_action[state_action == np.max(state_action)].index)
        else:
            # 直接选择随机的一个动作
            actions=list(range(4))
            action = np.random.choice(actions)
        return action

4、进行Q表中价值的学习更新

接下来就是最为关键的部分，即如何更新Q表中的值，我们依据的公式是：

在上述公式中我们可以通过如下代码或者类似的代码来访问到Q(s,a):

q_table.loc[s, a]

学习率alpha和折扣因子gamma是我们自定义的，下一个状态s_和立即回报reward都是env返还给我们的， 所以我们可以得到如下代码来实现：

    def learn(s, a, r, s_):
        """学习更新 Q-Table"""
        check_state_exist(s_)
        # 计算Q预测值
        q_predict = self.q_table.loc[s, a]
        # 计算Q现实值
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, :].max()  # 下一状态不是终点
        else:
            q_target = r  # 下一状态是终点
        # 更新
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)  # 更新Q-Table