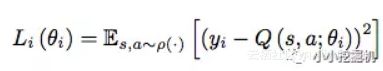DQN三大改进(二)-Prioritised replay
1、背景
这篇文章我们会默认大家已经了解了DQN的相关知识,如果大家对于DQN还不是很了解,可以参考文章https://www.jianshu.com/p/10930c371cac。
我们简单回顾一下DQN的过程(这里是2015版的DQN):
DQN中有两个关键的技术,叫做经验回放和双网络结构。
DQN中的损失函数定义为:
其中,yi也被我们称为q-target值,而后面的Q(s,a)我们称为q-eval值,我们希望q-target和q-eval值越接近越好。
q-target如何计算呢?根据下面的公式:
上面的两个公式分别截取自两篇不同的文章,所以可能有些出入。我们之前说到过,我们有经验池存储的历史经验,经验池中每一条的结构是(s,a,r,s'),我们的q-target值根据该轮的奖励r以及将s'输入到target-net网络中得到的Q(s',a')的最大值决定。
经验回放的功能主要是解决相关性及非静态分布问题。具体做法是把每个时间步agent与环境交互得到的转移样本 (st,at,rt,st+1) 储存到回放记忆单元,要训练时就随机拿出一些(minibatch)来训练。(其实就是将游戏的过程打成碎片存储,训练时随机抽取就避免了相关性问题)
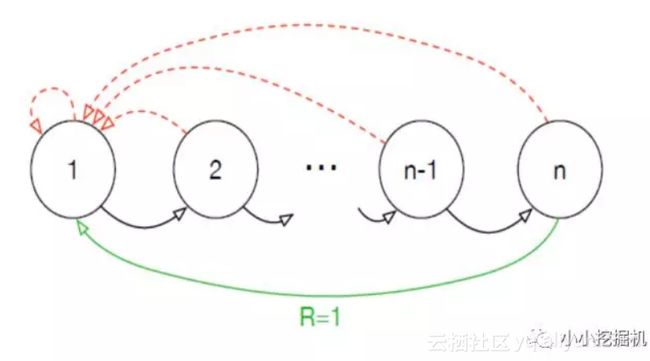
但是经验回放也存在一定的问题,在奖励十分少的时候,会出现学习速度非常慢的问题。在新的文章中,提出了一种“Blind Cliffwalk”的环境。来示例说明当奖赏非常rare的时候,探索所遇到的挑战。假设仅有 n 个状态,这个环境就要求足够的随机步骤知道得到第一个非零奖励;确切的讲,随机的选择动作序列就会有 2−n的概率才能得到第一个非零奖赏。此外,最相关的 transitions 却藏在大量的失败的尝试当中。“Blind Cliffwalk”环境如下图所示:
为了有效的解决上述的问题,提出了Prioritized replay的做法,我们先看看文中给出的算法流程:
这一套算法重点就在我们 batch 抽样的时候并不是随机抽样, 而是按照 Memory 中的样本优先级来抽. 所以这能更有效地找到我们需要学习的样本. 样本的优先级如何确定?我们可以用到 TD-error, 也就是 q-target - q-eval 来规定优先学习的程度. 如果 TD-error 越大, 就代表我们的预测精度还有很多上升空间, 那么这个样本就越需要被学习, 也就是优先级 p 越高.
优先级的计算基于如下公式:
式中的pi即我们计算的TD-error。
有了 TD-error 就有了优先级 p, 那我们如何有效地根据 p 来抽样呢? 如果每次抽样都需要针对 p 对所有样本排序, 这将会是一件非常消耗计算能力的事. 文中提出了一种被称作SumTree的方法。
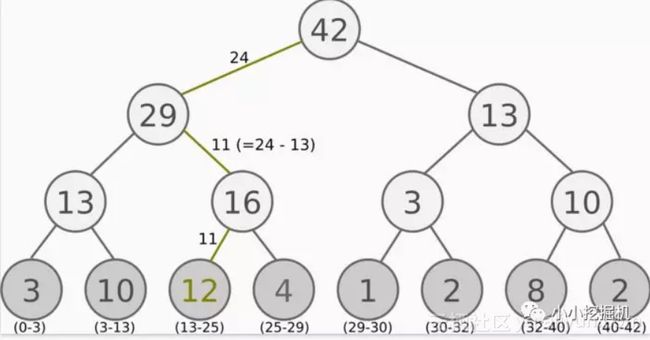
SumTree 是一种树形结构, 每片树叶存储每个样本的优先级 p, 每个树枝节点只有两个分叉, 节点的值是两个分叉的合, 所以 SumTree 的顶端就是所有 p 的合. 如下图所示。最下面一层树叶存储样本的 p, 叶子上一层最左边的 13 = 3 + 10, 按这个规律相加, 顶层的 root 就是全部 p 的合了.
抽样时, 我们会将 p 的总合 除以 batch size, 分成 batch size 那么多区间, (n=sum(p)/batch_size). 如果将所有 node 的 priority 加起来是42的话, 我们如果抽6个样本, 这时的区间拥有的 priority 可能是这样.
[0-7], [7-14], [14-21], [21-28], [28-35], [35-42]
然后在每个区间里随机选取一个数. 比如在第区间 [21-28] 里选到了24, 就按照这个 24 从最顶上的42开始向下搜索. 首先看到最顶上 42 下面有两个 child nodes, 拿着手中的24对比左边的 child 29, 如果 左边的 child 比自己手中的值大, 那我们就走左边这条路, 接着再对比 29 下面的左边那个点 13, 这时, 手中的 24 比 13 大, 那我们就走右边的路, 并且将手中的值根据 13 修改一下, 变成 24-13 = 11. 接着拿着 11 和 13 左下角的 12 比, 结果 12 比 11 大, 那我们就选 12 当做这次选到的 priority, 并且也选择 12 对应的数据.
2、代码实现
本文的代码还是根据莫烦大神的代码,它的github地址为:https://github.com/MorvanZhou/Reinforcement-learning-with-tensorflow
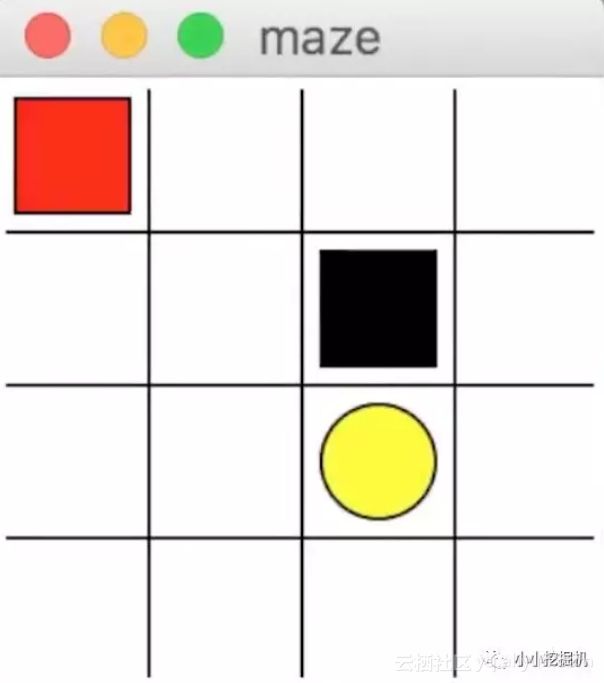
这里我们想要实现的效果类似于寻宝。
其中,红色的方块代表寻宝人,黑色的方块代表陷阱,黄色的方块代表宝藏,我们的目标就是让寻宝人找到最终的宝藏。
这里,我们的状态可以用横纵坐标表示,而动作有上下左右四个动作。使用tkinter来做这样一个动画效果。宝藏的奖励是1,陷阱的奖励是-1,而其他时候的奖励都为0。
接下来,我们重点看一下我们Prioritised replay Double-DQN相关的代码。
定义输入
在通过梯度下降法进行参数更新时,由于需要加入权重项,因此增加了ISWeigths这一个输入。
#---------------------input----------------------self.s = tf.placeholder(tf.float32,[None,self.n_features],name='s')self.q_target = tf.placeholder(tf.float32,[None,self.n_actions],name='Q_target')self.s_ = tf.placeholder(tf.float32, [None, self.n_features], name='s_')if self.prioritized: self.ISWeights = tf.placeholder(tf.float32,[None,1],name='IS_weights')
定义双网络结构
这里我们的双网络结构都简单的采用简单的全链接神经网络,包含一个隐藏层。这里我们得到的输出是一个向量,表示该状态才取每个动作可以获得的Q值:
def build_layers(s, c_names, n_l1, w_initializer, b_initializer, trainable):
with tf.variable_scope('l1'):
w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer, collections=c_names, trainable=trainable)
b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer, collections=c_names, trainable=trainable)
with tf.variable_scope('l2'):
w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer, collections=c_names, trainable=trainable)
b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer, collections=c_names, trainable=trainable)
out = tf.matmul(l1, w2) + b2 return out
接下来,我们定义两个网络:
# ---------------------eval net -----------------with tf.variable_scope('eval_net'):
c_names, n_l1, w_initializer, b_initializer = \
['eval_net_params', tf.GraphKeys.GLOBAL_VARIABLES], 20, \
tf.random_normal_initializer(0., 0.3), tf.constant_initializer(0.1) # config of layers self.q_eval = build_layers(self.s, c_names, n_l1, w_initializer, b_initializer, True)# --------------------target net----------------with tf.variable_scope('target_net'):
c_names = ['target_net_params', tf.GraphKeys.GLOBAL_VARIABLES] self.q_next = build_layers(self.s_, c_names, n_l1, w_initializer, b_initializer, False)
定义损失和优化器
接下来,我们定义我们的损失,和DQN一样,我们使用的是平方损失,但是此时我们的损失是有权重的!:
# --------------------loss and train -----------with tf.variable_scope('loss'): if self.prioritized: self.abs_errors = tf.reduce_sum(tf.abs(self.q_target - self.q_eval), axis=1) # for updating Sumtree self.loss = tf.reduce_mean(self.ISWeights * tf.squared_difference(self.q_target, self.q_eval)) else: self.loss = tf.reduce_mean(tf.squared_difference(self.q_target, self.q_eval))
with tf.variable_scope('train'): self._train_op = tf.train.RMSPropOptimizer(self.lr).minimize(self.loss)
定义SumTree类
定义完我们的网络结构之后,我们介绍两个辅助类,一个是用于Sample的SumTree类,另一个是用于记忆存储和读取的Memory类。
在初始化我们的SumTree类时,我们要定义好树的容量,即经验池的容量,以及用于存储优先级的tree结构和存储数据的data。tree结构我们使用一维数组实现,采取从上往下,从左往右的层次结构进行存储,同时,我们定义一个返回树根节点也就是树中叶子结点总优先级的函数。
def __init__(self,capacity): self.capacity = capacity self.data_pointer = 0 self.tree = np.zeros(2 * capacity - 1) self.data = np.zeros(capacity,dtype=object)
@propertydef total_p(self): return self.tree[0] # the root
接下来,我们定义一个用于添加数据的add函数,在添加数据的时候会触发我们的update函数,用于更新树中节点的值。
def add(self,p,data):
tree_idx = self.data_pointer + self.capacity - 1 self.data[self.data_pointer] = data self.update(tree_idx,p) self.data_pointer += 1 if self.data_pointer >= self.capacity: # replace when exceed the capacity self.data_pointer = 0
刚才提到了,在添加数据的时候,由于某个叶子结点的数值改变了,那么它的一系列父节点的数值也会发生改变,所以我们定义了一个update函数如下:
def update(self,tree_idx,p):
change = p - self.tree[tree_idx] self.tree[tree_idx] = p while tree_idx!=0:
tree_idx = (tree_idx - 1) // 2 self.tree[tree_idx] += change
最后,我们要定义一个根据数字来采样节点的算法,如何采样我们刚才已经介绍过了,即从头节点开始,每次决定往左还是往右,直到到达叶子结点为止,并返回叶子结点的id,优先级以对应的转移数据:
def get_leaf(self,v):
parent_idx = 0 while True:
cl_idx = 2 * parent_idx + 1
cr_idx = cl_idx + 1 if cl_idx >= len(self.tree):
leaf_idx = parent_idx break else: if v <= self.tree[cl_idx]:
parent_idx = cl_idx else:
v -= self.tree[cl_idx]
parent_idx = cr_idx
data_idx = leaf_idx - self.capacity + 1 return leaf_idx,self.tree[leaf_idx],self.data[data_idx]
定义Memory类
在初始化时,我们首先要定义好我们的参数:
def __init__(self, capacity): self.tree = SumTree(capacity) self.epsilon = 0.01 # small amount to avoid zero priority self.alpha = 0.6 # [0~1] convert the importance of TD error to priority self.beta = 0.4 # importance-sampling, from initial value increasing to 1 self.beta_increment_per_sampling = 0.001 self.abs_err_upper = 1. # clipped abs error
接下来,我们定义一个store函数,用于将新的经验数据存储到Sumtree中,我们定义了一个abs_err_upper和epsilon ,表明p的范围在[epsilon,abs_err_upper]之间,对于第一条存储的数据,我们认为它的优先级P是最大的,同时,对于新来的数据,我们也认为它的优先级与当前树中优先级最大的经验相同。
def store(self, transition):
max_p = np.max(self.tree.tree[-self.tree.capacity:]) if max_p == 0:
max_p = self.abs_err_upper self.tree.add(max_p, transition) # set the max p for new p
随后,我们定义了一个采样函数,根据batch的大小对经验进行采样,采样的过程如我们上面所讲的,调用的是tree.get_leaf方法。同时在采样的过程中,我们还要计算在进行参数更新时每条数据的权重,代码之中权重的计算是对原文中的公式进行了修改,如下图所示:
因此,我们的代码如下所示:
def sample(self,n):
b_idx,b_memory,ISWeights = np.empty((n,),dtype=np.int32),np.empty((n,self.tree.data[0].size)),np.empty((n,1))
pri_seg = self.tree.total_p / n self.beta = np.min([1., self.beta + self.beta_increment_per_sampling])
min_prob = np.min(self.tree.tree[-self.tree.capacity:]) / self.tree.total_p # for later calculate ISweight for i in range(n):
a, b = pri_seg * i, pri_seg * (i + 1)
v = np.random.uniform(a, b)
idx, p, data = self.tree.get_leaf(v)
prob = p / self.tree.total_p
ISWeights[i, 0] = np.power(prob/min_prob, -self.beta)
b_idx[i], b_memory[i, :] = idx, data return b_idx, b_memory, ISWeights
最后,我们还定义了一个更新树中权重的方法:
def batch_update(self, tree_idx, abs_errors):
abs_errors += self.epsilon # convert to abs and avoid 0
clipped_errors = np.minimum(abs_errors, self.abs_err_upper)
ps = np.power(clipped_errors, self.alpha) for ti, p in zip(tree_idx, ps): self.tree.update(ti, p)
选择action
选择action的代码没有变化,仍然采用e-greedy算法
def choose_action(self, observation):
observation = observation[np.newaxis, :] if np.random.uniform() < self.epsilon:
actions_value = self.sess.run(self.q_eval, feed_dict={self.s: observation})
action = np.argmax(actions_value) else:
action = np.random.randint(0, self.n_actions) return action
存储经验
由于我们定义了专门的Memory类,因此在存储经验的时候,直接调用该类的store方法即可。
def store(self,s,a,r,s_): if self.prioritized:
transition = np.hstack((s, [a, r], s_)) self.memory.store(transition) else: # random replay if not hasattr(self, 'memory_counter'): self.memory_counter = 0
transition = np.hstack((s, [a, r], s_))
index = self.memory_counter % self.memory_size self.memory[index, :] = transition self.memory_counter += 1
更新target-net
t_params = tf.get_collection('target_net_params')
e_params = tf.get_collection('eval_net_params')self.replace_target_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)]if self.learn_step_counter % self.replace_target_iter == 0: self.sess.run(self.replace_target_op) print('\ntarget_params_replaced\n')
选择batch
if self.prioritized:
tree_idx, batch_memory, ISWeights = self.memory.sample(self.batch_size)else:
sample_index = np.random.choice(self.memory_size, size=self.batch_size)
batch_memory = self.memory[sample_index, :]
更新网络参数
这里我们采用double-dqn的网络参数更新方法,这里有三点更新,首先,我们在训练的时候要同时计算我们的td-error,其次,每次训练之后,要根据td-error对树进行更新,最后,在计算误差的时候要考虑权重项。
q_next, q_eval = self.sess.run(
[self.q_next, self.q_eval],
feed_dict={self.s_: batch_memory[:, -self.n_features:], self.s: batch_memory[:, :self.n_features]})
q_target = q_eval.copy()
batch_index = np.arange(self.batch_size, dtype=np.int32)
eval_act_index = batch_memory[:, self.n_features].astype(int)
reward = batch_memory[:, self.n_features + 1]
q_target[batch_index, eval_act_index] = reward + self.gamma * np.max(q_next, axis=1)if self.prioritized:
_, abs_errors, self.cost = self.sess.run([self._train_op, self.abs_errors, self.loss],
feed_dict={self.s: batch_memory[:, :self.n_features], self.q_target: q_target, self.ISWeights: ISWeights}) self.memory.batch_update(tree_idx, abs_errors) # update priorityelse:
_, self.cost = self.sess.run([self._train_op, self.loss],
feed_dict={self.s: batch_memory[:, :self.n_features], self.q_target: q_target})self.cost_his.append(self.cost)self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_maxself.learn_step_counter += 1
3、参考文献
1、Prioritized Experience Replay (DQN) (Tensorflow):https://morvanzhou.github.io/tutorials/machine-learning/reinforcement-learning/4-6-prioritized-replay/
2、PRIORITIZED EXPERIENCE REPLAY:https://www.cnblogs.com/wangxiaocvpr/p/5660232.html