bp神经网络matlab代码_干货 | 智能算法之基于遗传算法的BP神经网络优化算法

算法简介

  BP神经网络是一类多层的前馈神经网络。BP 神经网络中的 BP 为 Back  Propagation 的简写，意为误差的反向传播。最早它是由Rumelhart、McCelland等科学家于 1986 年提出来的。Rumelhart 并在Nature 上发表了一篇非常著名的文章 《Learning representations by back-propagating errors》。由于BP算法结构简单、可调整参数多、训练算法也多，而且可操作性好，使它得到了非常广泛的应用。据统计，80%~90%的神经网络模型都是采用BP神经网络或者它的变形。BP神经网络是前向网络的核心部分，是神经网络中最精华、最完美的部分。

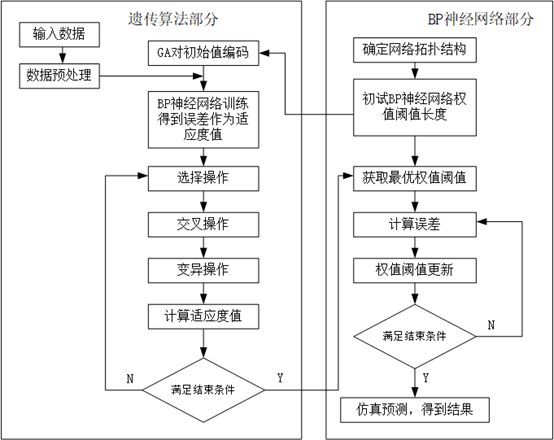
  BP神经网络虽然是人工神经网络中应用最广泛的算法，但也有其局限性，例如学习收敛速度太慢、不能保证收敛到全局最小点、网络结构不易确定。此外，网络结构、初始连接权值和阈值选择对网络训练的影响很大，但是又无法准确获得，针对这些特点可以采用遗传算法对神经网络进行优化。有关遗传算法的基本要素已经在前两次提及，此处不再赘述。遗传算法优化BP神经网络算法流程如下图：                 

图1 遗传算法优化BP神经网络算法流程图

  遗传算法优化BP神经网络主要分为BP神经网络结构确定、遗传算法优化权值及阈值和BP神经网络训练及预测3个部分。其中，BP神经网络结构确定部分根据样本输入/输出参数个数确定，进而确定遗传算法种群个体的编码长度。遗传算法优化使用遗传算法来优化BP神经网络的权值和阈值，只要网络结构已知，权值和阈值的个数就已知了。神经网络的权值和阈值一般是通过随机初始化为[-0.5,0.5]区间的随机数，这个初始化参数对网络训练的影响很大，但是又无法准确获得，对于相同的初始权值和阈值，网络的训练结果是一样的，引入遗传算法就是为了优化出最佳的初始权值和阈值。

案例介绍

  以某拖拉机的齿轮箱为工程背景，使用基于遗传算法的BP神经网络进行齿轮箱故障的诊断。统计表明，齿轮箱故障中60%左右都是由齿轮箱故障导致的，所以这里只研究齿轮的故障，这里选取频域中的几个特征量，频域中齿轮故障比较明显的是在啮合频率处的边缘带上。所以在频域特征信号的提取中选取了在2、4、6挡，在1、2、3轴的边频带族fs±nfz处的幅值Ai,j1、Ai,j2和Ai,j3，其中fs为齿轮的啮合频率，fz为轴的转频，n=1,2,3, i=2,4,6表示档位j=1,2,3表示轴的序号，由于在2轴和3轴上有两对齿轮啮合，所以1、2分别表示两个啮合频率。这样，网络的输入就是一个15维的向量。因为这些数据具有不同的量纲和量级，所以在输入神经网络之前首先进行归一化处理。

齿轮箱状态数据样本：

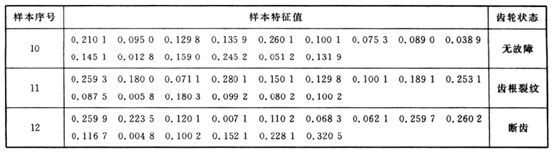
表1 齿轮箱状态样本数据

  从表中可以看出齿轮状态分为三种故障模式，因此可以采用如下的形式来表示输出：无故障(1,0,0)、齿根裂纹(0,1,0)、断齿(0,0,1)

  为了对训练好的网络进行测试，再增加三组测试数据作为网络的测试数据，如下：

表2 测试样本数据

算法实现

1. 神经网络算法实现

(1) 网络创建

  BP网络结构的确定有以下两条比较重要的指导原则。

a) 对于一般的模式识别问题，三层网络可以很好地解决问题；

b) 在三层网络中，隐含层神经网络个数n2和输入层神经元个数n1之间有近似关系：

         n2 = 2 * n1 +1。

  本案例中，由于样本有15个输入参数，3个输出参数，所以这里n2取值为31，设置的BP神经网络 结构为15-31-3，即输入层有15个节点，隐含层有31个节点，输出层有3个节点，因此总有15*31+31*3=558个权值(边)，31+3=34个阙值，所以遗传算法优化参数的个数为558+34=592。使用训练数据进行网络训练，使用测试数据对训练后的网络进行测试。把测试样本的测试误差范数作为衡量网络的泛化能力，再通过误差范数计算个体的适应度值，个体的误差范数越小，个体适应度值越大，该个体越优。

  神经网络的隐含层神经元传递函数采用S型正切函数tansig()，输出层神经元的传递函数采用S型对数函数logsig()，这是由于输出模式为0-1，正好满足网络的输出要求。假定输入样本矩阵为P，创建网络可以使用如下代码：

(2) 网络训练和测试

  网络训练是一个不断修正权值和阙值的过程，通过训练，使得网络的输出误差越来越小。在默认情况下，BP神经网络的训练函数为trainlm()，即是利用Levenberg-Marquardt算法对网络进行训练，具体的网络参数设置和训练代码如下：

  网络训练之后，需要对网络进行测试。例如测试样本数据矩阵为P_test，则测试代码如下：

2.  遗传算法实现

  遗传算法优化BP神经网络是用遗传算法来优化BP神经网络的初始权重值和阙值，使优化后的BP神经网络能够更好地进行样本预测。

(1)种群初始化

  个体编码使用二进制编码，每个个体均为一个二进制串，由输入层与隐含层连接权值、隐含层阙值、输出层连接权值、输出层阙值四部分组成，每个阙值和权值都使用二进制编码，将所有权值和阙值的编码连接起来即为个体的编码。例如，本例的网络结构是15-31-3，所以权值和阈值的个数如下表：

  假设权值和阙值的编码均为10位二进制数，那么个体的总编码长度为5920位(465+31+93+3=592)。前4650位为输入层与隐含层连接权值编码；4651~4960位为隐含层阙值编码；4961~5890位为隐含层与输出层连接权值编码；5891~5920位为输出层阙值编码。

(2) 适应度函数

  本案例是为了使BP网络在预测时，预测值与期望值的残差尽可能小，所以选择预测样本的预测值与期望值的误差矩阵的范数作为目标函数的输出。

适应度函数采用排序的适应度分配函数：FitnV = ranking(obj)，其中obj为目标函数的目标值。

(3) 选择算子

  采用随机遍历抽样(sus 轮盘赌算法)。

(4) 交叉算子

  采用最简单的单点交叉算子。

(5) 变异算子

  变异以一定的概率产生变异基因树，用随机方法选择发生变异的基因，如果所选基因的编码为1，则变为0，反之，则变为1。

本案例的遗传算法运行参数设定如下表：

3. MATLAB程序实现

  在MATLAB软件中编程实现基于遗传算法优化的BP神经网络齿轮箱故障诊断算法，遗传算法部分使用Sheffield遗传算法工具箱，BP神经网络部分使用MATLAB自带的神经网络工具箱。

神经网络部分代码:

遗传算法主函数

遗传算法主函数流程为
步骤1：随机初始化种群；
步骤2：计算种群适应度值，从中找出最优个体；
步骤3：选择操作；
步骤4：交叉操作；
步骤5：变异操作；
步骤6：判断进化是否结束，若否，则返回步骤2.[P1] [sj2] 
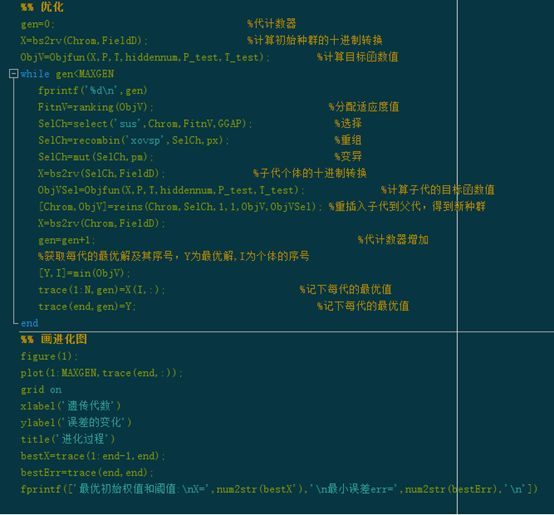
主函数MATLAB代码如下：  

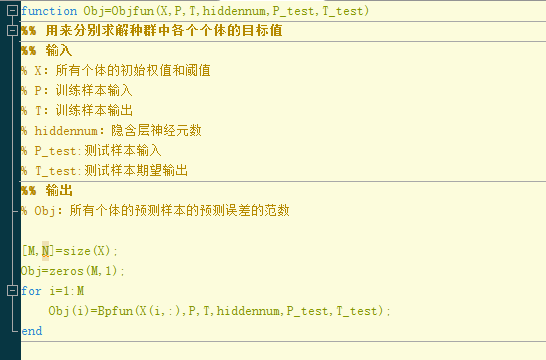
其中，函数Objfun的代码如下：

比较使用遗传算法前后的差别代码：

结果分析

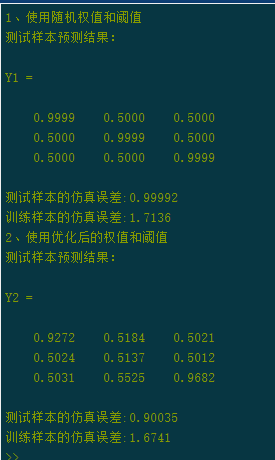
运行主函数的输出结果：

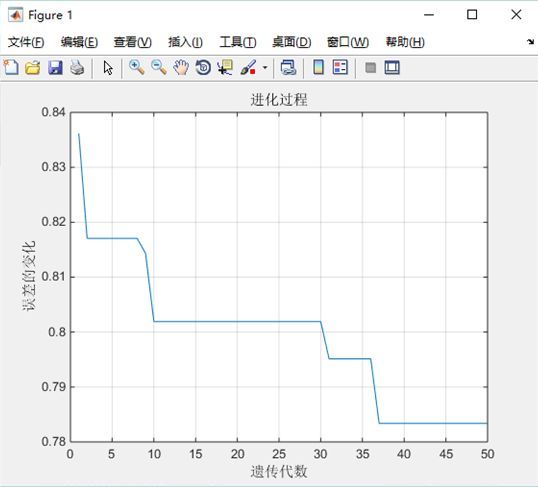
得到的进化曲线如下：

得到最优初始值和阈值后，运行对比函数，所得结果如下：

  通过比较可以看出，优化初始权值和阈值后的测试样本误差由0.99992减少到0.90035，训练样本的误差由1.7136减少到1.6741。BP网络的训练和预测样本的测试效果都得到了一定的改善。

参考文献：

郁磊,史峰,王辉,胡斐.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2015.

数字地形周刊整理

文案 | 蒋尚婧

编辑 | 李思进

校对| 刘海龙