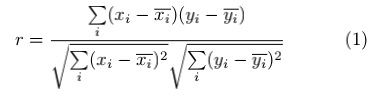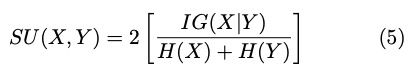特征工程-Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution

Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution

2003

Lei Yu [email protected]

Huan Liu [email protected]

Department of Computer Science & Engineering, Arizona State University, Tempe, AZ 85287-5406, USA

Abstract

特征选择作为机器学习的一个预处理步骤，可以有效地降低维数，去除无关数据，提高学习精度，提高结果的可理解性。然而，近年来数据维数的增加对现有的特征选择方法的效率和有效性提出了严峻的挑战。在这项工作中，我们引入了一个新的概念，优势相关，并提出了一种快速滤波方法，可以识别相关特征以及相关特征之间的冗余，而无需进行成对相关分析。通过与其他方法的比较，证明了该方法的有效性和有效性。

1. Introduction

特征选择是机器学习中常用的预处理步骤。它是一个选择原始特征子集的过程，从而使特征空间按一定的评价准则进行最优约简。自20世纪70年代以来，特征选择一直是研究和开发的一个多产领域，并被证明能有效地去除不相关和冗余的特征，提高学习任务的效率，提高学习绩效，如预测准确性，以及增强学习结果的可理解性（Blum&Langley，1997；Dash&Liu，1997；科哈维和约翰，1997）。近年来，在基因组计划（Xing et al.，2001）、文本分类（Yang&Pederson，1997）、图像检索（Rui et al.，1999）和客户关系管理（Ng&Liu，2000）等许多应用中，数据在实例数量和特征数量上都变得越来越大。这一巨大问题可能会导致许多机器学习算法在可伸缩性和学习性能方面出现严重问题。例如，高维数据（即具有数百或数千个特征的数据集）可能包含高度不相关和冗余的信息，这可能极大地降低学习算法的性能。因此，在面对高维数据的今天，特征选择成为机器学习的一个重要任务。然而，这种尺寸和维数的巨大趋势也对特征选择算法提出了严峻的挑战。最近在特征选择方面的一些研究工作集中在这些挑战上，从处理大量实例（Liu et al.，2002b）到处理高维数据（Das，2001；Xing et al.，2001）。本文主要研究高维数据的特征选择问题。下面，我们首先回顾特征选择模型并解释为什么过滤器解决方案适用于高维数据，然后回顾最近在高维数据的特征选择方面所做的一些工作。

特征选择算法分为两大类，filter（滤波器）模型或wrapper模型（Das，2001；Kohavi&John，1997）。该filter模型依赖于训练数据的一般特征来选择一些特征，而不涉及任何学习算法。wrapper模型在特征选择中需要一个预先挖掘的学习算法，并使用其性能来评估和确定选择了哪些特征。对于每个新的特征子集，wrapper模型需要学习一个假设（或分类器）。它倾向于找到更适合于预定学习算法的特征，从而产生更好的学习性能，但它也倾向于比filter模型更昂贵的计算（Lan gley，1994）。当特征个数很大时，由于其计算效率，通常选择filter模型。

为了结合两种模型的优点，最近提出了混合模型中的算法来处理高维数据（Das，2001；Ng，1998；Xing等人，2001）。在这些算法中，首先使用基于数据特征的特征子集的优度度量来选择给定基数的最佳子集，然后利用交叉验证来确定不同基数的最终最佳子集。这些算法主要集中在结合filter和wrapper算法，以达到最佳的性能与特定的学习算法具有相似的时间复杂度的filter算法。本文以filter模型为研究对象，提出了一种新的特征选择算法，该算法能有效地去除不相关和冗余特征，且计算量小于现有算法

在第二节中，我们回顾了滤波器模型中的现有算法，并指出了它们在高维背景下的问题。在第3节中，我们描述了相关度量，这些度量构成了我们评估特征相关性和冗余的方法的基础。在第四节中，我们首先提出了一种新的基于优势相关的特征选择方法，然后提出了一种时间复杂度小于二次方的快速算法。在第五节中，我们通过在各种真实数据集上的大量实验，与其他具有代表性的特征选择算法进行比较，评估了该算法的效率和有效性，并讨论了研究结果的意义。在第6节中，我们用一些可能的扩展来结束我们的工作。

2. Related Work

在滤波器模型中，不同的特征选择算法可以进一步分为两类，即特征加权算法和子集搜索算法，根据它们是单独评价特征的优劣，还是通过特征子集来评价特征的优劣。下面，我们将讨论每组中具有代表性的算法的优缺点。特征加权算法分别为特征分配权重，并根据它们与目标概念的相关性对它们进行排序。机器学习文献中对特征相关性有许多不同的定义（Blum&Langley，1997；Kohavi&John，1997）。一个特征是好的，因此如果它的相关权重大于一个阈值，就会被选中。一个依赖于相关性评估的著名算法是Relief（Kira&Rendell，1992）。Relief的关键思想是根据特征值在相邻的同一类和不同类的实例之间的区分程度来估计特征的相关性。Relief从训练集中随机抽取m个实例，并基于所选实例与相同类和相反类的最近两个实例之间的差异来更新每个特征的相关性估计。对于具有M个实例和N个特征的数据集，Relief的时间复杂度为O（mMN）。当m为常数时，时间复杂度变为O（MN），这使得它对于具有大量实例和很高维数的数据集具有很强的可伸缩性。但是，Relief无助于删除冗余特性。只要特征被认为与类概念相关，它们都将被选择，即使它们中的许多彼此高度相关（Kira&Rendell，1992）。这组中的许多其他算法都有与Relief类似的问题。它们只能捕获特征与目标概念的相关性，而不能发现特征之间的冗余。然而，来自特征选择文献的经验证据表明，除了不相关的特征外，冗余特征也会影响学习算法的速度和准确性，因此也应予以消除（Hall，2000；Kohavi&John，1997）。因此，在高维数据特征选择的背景下，单纯的基于相关性的特征加权算法不能很好地满足特征选择的需要。

子集搜索算法在一定的评估方法（Liu&Motoda，1998）的指导下搜索候选特征子集，该方法捕获每个子集的优点。当搜索停止时，将选择最优（或接近最优）子集。一些现有的评估指标在去除不相关和冗余特征方面表现出了有效性，包括一致性指标（Dash等人，2000）和相关性指标（Hall，1999；Hall，2000）。一致性度量试图找到尽可能一致地分离类的最少数量的特性。不一致性定义为两个实例具有相同的特征值，但类标签不同。在Dash等人（2000）中，不同的搜索策略，即穷举搜索、启发式搜索和随机搜索，与这种评估方法相结合，形成不同的算法。穷举搜索的时间复杂度与数据维数呈指数关系，启发式搜索的时间复杂度与数据维数呈二次关系。在随机搜索中，复杂度可以与迭代次数成线性关系，但实验表明，为了找到最佳特征子集，所需的迭代次数通常至少是特征数的二次方（Dash et al.，2000）。在Hall（2000）中，基于一个好的特征子集是一个包含与类高度相关但彼此不相关的特征的子集的假设，应用相关度量来评估特征子集的优度其他的。那个底层算法CFS也利用了启发式搜索。因此，现有的子集搜索算法在维数方面具有二次或更高的时间复杂度，因此在处理高维数据时不具有很强的可扩展性。为了克服这两类算法存在的问题，满足高维数据特征选择的需要，本文提出了一种新的特征选择算法与子集搜索算法相比，该算法能以较低的时间复杂度有效地识别无关特征和冗余特征。

3. Correlation-Based Measures

在本节中，我们将讨论如何评估用于分类的特征的优度。一般来说，一个特性是好的，如果它是相关的类概念，但不是多余的任何其他相关的功能。

如果我们采用两个变量之间的相关性作为优度度量，那么上面的定义就是，如果一个特征与类高度相关，但与其他任何特征都不高度相关，那么它就是好的。换言之，如果特征和类别之间的相关性足够高，使其与类别相关（或预测），并且特征和任何其他相关特征之间的相关性没有达到可以由任何其他相关特征预测的水平，它将被视为分类任务的一个好特征。从这个意义上说，特征选择的问题归结为找到一个合适的度量特征之间的相关性和一个合理的程序来选择基于这个度量的特征。测量两个随机变量之间相关性的方法大致有两种。一种是基于经典的线性相关，另一种是基于信息论。在第一种方法中，最著名的度量是线性相关系数。对于一对变量（X，Y），线性相关系数r由公式给出：

其中是X的平均值，是Y的平均值。r的值介于-1和1之间（包括-1和1）。如果X和Y完全相关，r取1或-1；如果X和Y完全独立，r为-1零。是的是两个变量的对称度量。这一类中的其他度量基本上是上述公式的变体，例如最小二乘回归误差和最大信息压缩指数（Mitra等人，2002）。选择线性相关作为分类的特征优度度量有很多好处。首先，它有助于去除与类几乎零线性相关的特征。其次，它有助于减少所选特征之间的冗余。众所周知，如果数据在原始表示中是线性可分的，那么如果除去一组线性相关特征中的一个以外的所有特征，则数据仍然是线性可分的（Das，1971）。然而，在现实世界中总是假设特征之间存在线性相关性是不安全的。线性相关性度量可能无法捕获本质上不是线性的相关性。另一个限制是，计算要求所有特征都包含数值值。为了克服这些缺点，在我们的解决方案中，我们采用了另一种方法，并根据熵的信息理论概念选择了一种相关度量，这是一种对随机变量不确定性的度量。变量X的熵定义为：

观察另一变量Y的值后，X的熵定义为：

其中p（Xi）是所有x值的先验概率，p（xi|yi）是给定y值的x的后验概率。X的熵减少的量反映了Y提供的关于X的附加信息，称为信息增益（Quinlan，1993），由

根据该度量，如果，则特征Y被认为与特征X的相关性大于与特征Z的相关性。关于信息增益测度，我们有如下定理。

定理:两个随机变量X和Y的信息增益是对称的。

证明草图：要证明，我们需要证明。这可以很容易地从得出。

对称性是衡量特征之间相关性的理想属性。然而，信息增益偏向于具有更多价值的特征。此外，必须对值进行规范化,以确保它们具有可比性，并具有相同的影响。因此，我们选择对称不确定度（Press等人，1988），定义如下:

它补偿了信息增益对具有更多值的特征的偏移，并将其值归一化到范围[0，1]，其中值1表示对其中一个值的了解完全预测另一个的值，值0表示X和Y是独立的。此外，它仍然对称地处理一对特征。基于熵的度量需要名义特征，但如果事先对值进行适当的离散化，它们也可以用于度量连续特征之间的相关性（Fayyad&Irani，1993；Liu et al.，2002a）。因此，我们在这项工作中使用了对称不确定性。

4. A Correlation-Based Filter Approach

4.1. Methodology

使用对称不确定性（SU）作为优度度量，我们现在准备开发一个基于特征（包括类）的相关分析来选择好的特征进行分类的过程。这涉及到两个方面：（1）如何判断一个特征是否与类相关；（2）如何判断一个相关特征与其他相关特征是否冗余。第一个问题的答案可以是使用用户定义的阈值SU值，就像许多其他特征加权算法（例如，Relief）所使用的方法一样。更具体地说，假设一个数据集S包含N个特征和一个类C，表示度量特征Fi和类C之间相关性的SU值（称为C-相关），则相关特征的子集可以由阈值SU值δ决定，使得第二个问题的答案更复杂，因为它可能涉及所有特征之间的成对相关性分析（称为F相关），这导致大多数现有算法的时间复杂度为O（N2）与特征数N相关。

为了解决这个问题，我们提出下面的方法。由于F相关也被SU值捕获，为了确定相关特征是否冗余，我们还需要找到一种合理的方法来确定F相关的阈值水平。换言之，我们需要确定中两个特征之间的相关性水平是否足够高，从而导致冗余，从而可以从中删除其中一个特征。对于中的特征Fi，的值量化了Fi与c类相关（或预测）的程度。如果我们检查的的值，我们还将获得关于Fi与中其他相关特征相关（或预测）的程度的量化估计。因此，可以用与我们决定相同的直接方式，使用等于或类似于δ的阈值SU值，来识别与Fi高度相关的特征。我们可以对中的所有特征这样做。然而，只有当我们试图确定一个概念的高度相关特征而不考虑另一个概念时，这种方法听起来才合理。在已经为类概念确定的一组相关特征的上下文中，当我们试图确定内给定特征Fi的高度相关特征时，使用Fi和类概念之间的C相关水平作为一个更合理的方法参考文献原因在于一个共同的现象，即在某个层次上与一个概念（例如，类）相关联的，也可以在同一层次或更高层次上与其他一些概念（特征）相关联的。因此，即使该特征与类概念之间的相关性大于某个阈值δ并且因此使得该特征与类概念相关，该相关性也决不是主要的。更准确地说，我们将优势相关的概念定义如下。

定义1（主要相关）特征Fi (Fi∈S)与C类之间的相关性主要，不存在的Fj。

如果特征Fi存在这样的Fj，我们称其为a 对Fi的冗余对等体，并使用SPi表示该集合 所有冗余对等体的Fi。给定和我们把分成两个部分，和，，。

定义2（主要特征）如果特征与类的相关性是主要的，或者在移除冗余对等点后可以成为主要的，则特征对类是主要的。

根据上述定义，如果一个特征在预测类概念时占优势，那么它就是好的，而分类特征选择是一个将所有占优势的特征识别为类概念并去除其余特征的过程。我们提出了三种启发式算法，它们可以有效地识别主要特征并去除所有相关特征中的冗余特征，而不必识别S′中每个特征的所有冗余对等点，从而避免了对所有相关特征之间的F相关进行成对分析。

我们在开发这些启发式算法时的假设是，如果发现两个特征彼此冗余，并且其中一个需要删除，则删除与类概念不太相关的特征可以保留更多信息来预测类，同时减少数据中的冗余。

启发式1，将F作为主要特征，删除中的所有特征，并跳过为它们识别冗余对等体。

启发式2，在对F做出决定之前，处理中的所有特征。如果没有一种方法占主导地位，就遵循启发式方法1;否则，只删除Fi，并根据S '中的其他特性来决定是否删除中的特性。

启发式3（起始点）值最大的特征总是一个主要特征，可以作为删除其他特征的起点。

4.2. Algorithm and Analysis

在此基础上，我们开发了一种快速相关滤波器(FCBF)算法。如图1所示，给定一个数据集.

对于N个特征和一个类C，该算法为类概念找到一组最重要的特征。它由两个主要部分组成。在第一部分（第2-7行），它计算每个特征的SU值，根据预定义的阈值δ将相关特征选择到中，并根据SU值按降序排列。在第二部分（第8-20行）中，它进一步处理有序列表，去除冗余特征，只保留所有选定的相关特征中的优势特征。根据启发式1，已经被确定为主要特征的特征F总是可以用来过滤出排名低于Fp的其他特征，并且Fp是其冗余对等点之一。迭代从（第8行）中的第一个元素（启发式3）开始，并继续如下。对于所有剩余的特征（从Fp的右边到中的最后一个），如果Fp恰好是特征Fq的冗余对等，Fq将从中移除（启发式2）。在基于Fp的一轮特征过滤之后，算法将以Fp旁边的当前剩余特征作为新的参考（第19行），重复过滤过程。算法停止，直到没有更多的特征要从中删除。

上述算法的第一部分对于特征数N具有线性时间复杂度。至于第二部分，在每一次迭代中，使用上一轮识别的主要特征Fp，FCBF可以去除大量在当前迭代中与Fp冗余的特征。最好的情况可能是在排名列表中Fp后面的所有剩余特性都将被删除；最坏的情况可能是它们都没有。平均而言，我们可以假设在每次迭代中，剩下的一半特征将被删除。因此，就N而言，第二部分的时间复杂度是O(NlogN）。由于一对特征的SU的计算就数据集中的实例数M而言是线性的，因此FCBF的总体复杂度是O(MNlogN）。

5. Empirical Study

本节的目的是评估我们提出的算法的速度，选择的特征的数量，以及对选择的特征的学习精度。

5.1. Experiment Setup

在实验中，我们选取了三种具有代表性的特征选择算法，并与FCBF算法进行了比较。一种是特征加权算法ReliefF（一种扩展到ReliefF的算法），它搜索几个对噪声有鲁棒性的最近邻并处理多个类（kononeko，1994）；另两种是子集搜索算法，它利用顺序前向搜索并利用相关度量或一致性度量来指导搜索，分别表示为CorrSF和ConsSF。CorrSF是第2节中提到的CFS算法的变体。我们之所以选择CorrSF而不是CFS，是因为Hall（1999）的实验和我们的初步实验都表明CFS只比CorrSF产生稍好的结果，但是基于序贯前向搜索的CorrSF比基于5节点展开的最佳优先搜索的CFS运行得更快，因此更适合于高维数据。除了特征选择算法之外，我们还选择了两种不同的学习算法C4.5（Quinlan，1993）和NBC（Witten&Frank，2000）来评估每种特征选择算法对所选特征的准确性。

实验使用Weka对所有现有算法的实现进行，FCBF也在Weka环境中实现（Witten&Frank，2000）。总共有10个数据集是从UCI机器学习库（Blake&Merz，1998）和UCI KDD档案库（Bay，1999）中挑选出来的。数据集摘要见表1。

对于每个数据集，我们分别运行FCBF、ReliefF、CorrSF、ConsSF四种特征选择算法，并记录每种算法的运行时间和选择的特征数。然后，我们对原始数据集以及每个新获得的数据集应用C4.5和NBC，这些数据集只包含每个算法中选定的特征，并通过10倍交叉验证记录总体精度。

5.2. Results and Discussions

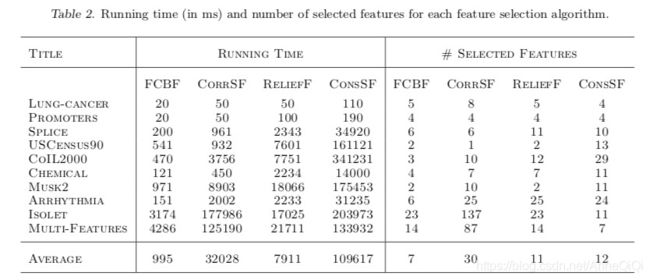
表2记录了每种特征选择算法的运行时间和选择的特征数量。对于ReliefF，在整个实验过程中，参数k设置为5 (neighbors)， m设置为30 (instances)。

从表2可以看出，对于每种算法，在不同数据集上的运行时间与我们之前的时间复杂度分析是一致的。从表2最后一行的平均值可以看出，FCBF的运行速度明显快于其他三种算法（以度为单位），这验证了FCBF优越的计算效率。有趣的是，ReliefF的速度出人意料地慢，即使它的时间复杂度在固定的样本大小M下变为O（mn）。原因在于搜索最近邻涉及距离计算，这比对称不确定值的计算更耗时。

从表2中也可以清楚地看出，FCBF通过选择最少数量的特征（USCensus90中只有一个例外）来实现最高级别的降维，这与我们对FCBF识别冗余特征能力的理论分析是一致的。

表3和表4分别显示了C4.5和NBC在不同特征集上的学习精度。从所有数据集的平均精度来看，我们观察到，一般而言，（1）FCBF提高了C4.5和NBC的精度；（2）在其他三种算法中，只有CorrSF可以将C4.5的精度提高到与FCBF相同的水平。从单个精度值来看，我们还观察到，对于大多数数据集，FCBF可以保持甚至提高精度。

上述实验结果表明，FCBF方法对于高维数据分类的特征选择是可行的。它能有效地实现高维降维，提高分类精度。

6. Conclusions

本文提出了一种新的优势相关概念，介绍了一种有效的特征冗余分析方法，并设计了一种快速相关滤波方法。通过大量实验，实现了一种新的特征选择算法FCBF，并与相关的特征选择算法进行了比较。通过对有特征选择和无特征选择的数据应用两种不同的分类算法，进一步验证了特征选择的结果。我们的方法证明了它在处理高维数据进行分类时的效率和有效性。我们进一步的工作将FCBF扩展到更高维度的数据（数千个特征）。我们将更详细地研究冗余特征及其在分类中的作用，并将FCBF与特征离散化算法相结合，以平滑地处理不同特征类型的数据。