深度学习中的语音处理

语音信号的多种表示形式

在计算机世界中，语音信号有多种表示形式。最常见的是音频文件，如1.mp3，2.wav，3.wma等。这些音频文件直接或间接记录声音的波形信息，虽然便于计算机快速处理和解码，但并不便于被神经网络使用和学习。通过引入适当的声学变换，在尽可能保留原语言信息的同时，把声音表示成便于神经网络使用的形式。

音频文件

wav格式
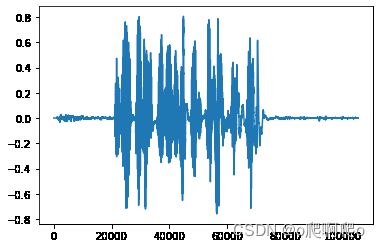
wav格式被称为波形文件，其保存声音的方法是：对声音连续波形经过采样（按一定采样频谱）、量化、编码（按一定采样位数）后得到声波的数字表示。这种表示相当于一组一维的数字，直接记录波形（整体可以认为是一个向量）。对于神经网络而言，如果使用这种表示作为输入，会存在向量过长的问题。因此，通常会借鉴图片处理的思路，通过卷积层（Conv1D）进行特征提取和长度压缩。
mp3格式等
以mp3格式为例。mp3是一种音频压缩算法，它利用人耳对高频声音不敏感的特性，把时域信号转化为频域信号，并对高频成分给予更高压缩比，实现约十倍压缩。同时，相比原始声音，人耳并不会感到明显的失真。虽然mp3文件体积更小，但一些音频处理工具不支持这种格式。因此，对于音频文件以wav格式最为常用。

梅尔频谱

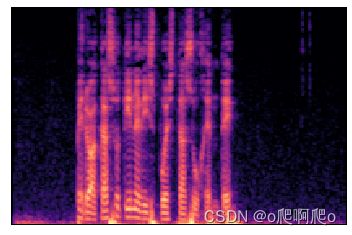
频谱是声音信号的频域表示，由时域信号经傅里叶变换（FT）而得，绘制成图像就是幅频图（除振幅图外还可做功率图）。由于语音的频谱是动态变化的，所以常采用离散时间（本身是离散数据）短时傅里叶变换（STFT）进行时频变换。由于使用短时变换，所以要对原始信号进行分帧、加窗（增加帧左端和右端的连续性，例如汉明窗函数）操作。经过这一操作后，原信号被切割为帧。例如：原始信号为（10000），经过帧长度为1000（假设帧间不重叠）的分帧操作后，变为（10 * （1000））。分帧后，对每一个短帧进行快速傅里叶变换（FFT），得到这一帧的线性频率振幅谱。在时间方向上，对每一帧的频谱进行拼接，得到整个声音的频谱图。它本质上是一个可以画在空间坐标系下的二元函数，只是频谱图中用颜色深浅来表示振幅或能量的大小。例如，每一帧在频率域被变换成50个离散频率，则上述声音信号可以画成高50，长10的频谱图。更加常用的是对数频谱图，它对振幅值做对数计算，相对压低高幅的振幅，以便观察低幅区的信号，其振幅单位为分贝dB。

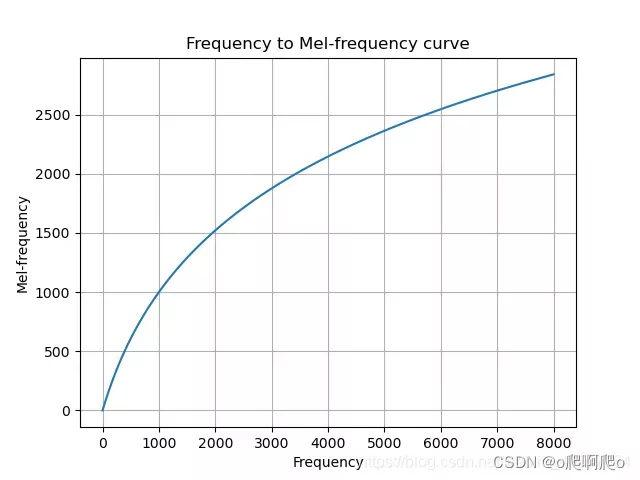
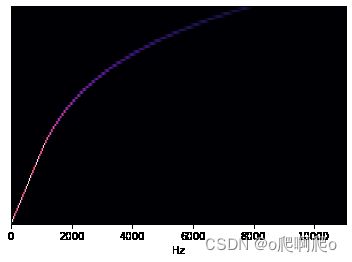
所谓梅尔频谱，是结合了人耳对声音的分辨能力，对原来的频率域进行变换，变成梅尔频率。人耳对低频声音的分辨要好于高频声音，相同的音调差（人耳分辨）在频率上的差值并不相同。对原始频率域进行变换，使得得到的新刻度上相等距离的两对频度，对于人耳来说也相等，就得到梅尔频度。显然，它是一个经验的刻度。很多经验函数可以表征梅尔频度和原始频度之间的关系，它们使二者在低频区呈线性关系，在高频区呈对数变化（压平）。下面的经验函数就是一个很好的关系变换：

$$m=2595{\text{log}}_{10}\left(1+\frac{f}{700}\right)$$

通过这样的变换，原始的频率域被变成梅尔频率。这些看似等距（在mel刻度下）的频率间隔在原始频率域上并不等距，能在有限的空间内保留原始语音的更多信息。梅尔滤波器组（Filter Bank）是对原始频率域的过滤，原始频率经过梅尔滤波器组后得到得到梅尔刻度下的频率-振幅（能量）信息。对梅尔滤波器组，通常取n=80。对数梅尔频谱，就是在此基础上对振幅做对数得到的频谱。

梅尔倒谱

倒谱（Cepstrum←Spectrum）是对数频谱进行傅里叶逆变换得到的结果，能解决梅尔滤波器组之间存在的相关性（如下图所示）并产生压缩表示。梅尔频率倒谱系数（MFCC）是在对数梅尔频谱的基础性，应用离散余弦变换（DCT）得到的结果。MFCC阶数表示保留的系数个数，通常从DCT变换结果的第2个系数开始选取。通常，MFCC占用的空间更小。

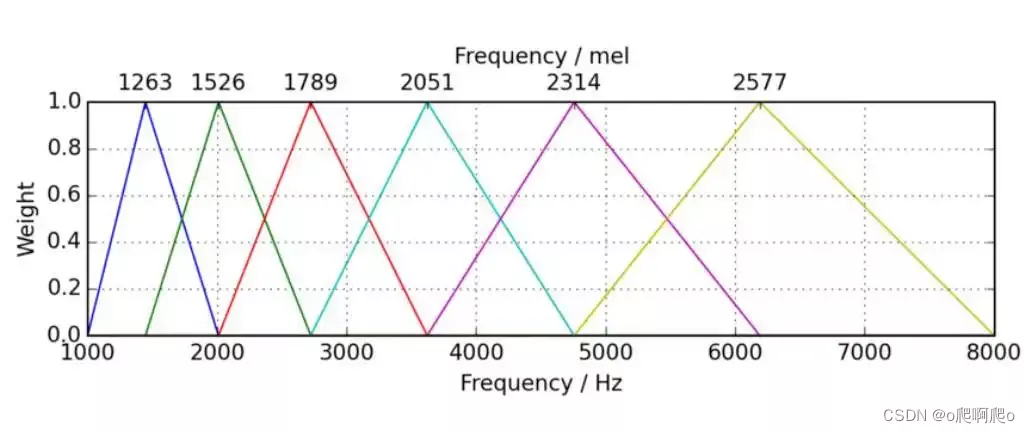
在深度学习下，神经网络不太容易受到高度相关输入的影响（传统的机器学习方法容易受到这种影响）。因此，人们开始质疑DCT计算的必要性，更多地转而使用梅尔频谱而不是MFCC。

频谱与倒谱的对比

从以下几个方面做对比¹：

• 计算量：MFCC是在对数频谱（FBank）的基础上进行的，所以MFCC的计算量更大
• 特征区分度：FBank特征相关性较高（相邻滤波器组有重叠），MFCC具有更好的判别度，这也是在大多数语音识别论文中用的是MFCC，而不是FBank的原因
• 信息量：FBank特征的提取更多的是希望符合声音信号的本质，拟合人耳接收的特性。MFCC做了DCT去相关处理，因此Filter
  Banks包含比MFCC更多的信息
• 神经网络可以更好的利用Filter Banks特征的相关性，降低信息损失。
  

什么是Delta与DeltaDeltas

Delta和Delta-deltas，很多人翻译成一阶差分和二阶差分，也被称为微分系数和加速度系数。使用它们的原因是，MFCC只是描述了一帧语音上的能量谱包络，但是语音信号似乎有一些动态上的信息，也就是MFCC随着时间的改变而改变的轨迹。有证明说计算MFCC轨迹并把它们加到原始特征中可以提高语音识别的表现。²

常用处理工具

这里介绍python中的音频处理包，包括其常用函数及其使用方法。

librosa

加载音频

import librosa
path = "1.wav"
audio, sr = librosa.load(path, sr=22050, mono=True, offset=0.0, duration=None)
# [ 0.0000000e+00  0.0000000e+00  0.0000000e+00 ... -3.0517578e-05  -6.1035156e-05  -3.0517578e-05]
# 22050

重采样

audio_after = librosa.resample(audio, orig_sr=22050, target_sr=16000, fix=True, scale=False)
print(audio_after)
# [ 0.0000000e+00  0.0000000e+00  0.0000000e+00 ... -4.6203029e-05  -4.5894383e-05  0.0000000e+00]

读取音频时长

d = librosa.get_duration(audio, sr=22050, S=None, n_fft=2048, hop_length=512, center=True)
print(d)
# 0 < win_length <= n_fft
# 4.776009070294784

采样率

sr = librosa.get_samplerate(path)
print(sr)
# 22050

读取过零率

zcr = librosa.feature.zero_crossing_rate(audio, frame_length=2048, hop_length=512, center=True)
print(zcr)
# 返回每一帧的过零率
[[0.00244141 0.02685547 0.02880859 0.03027344 0.03027344 0.00683594
  0.00732422 0.00634766 0.00683594 0.01708984 0.01660156 0.01611328
  0.01513672 0.01074219 0.01074219 0.01367188 0.01269531 0.01318359
  0.01367188 0.02587891 0.02587891 0.01953125 0.01904297 0.01953125
  0.03027344 0.02978516 0.04345703 0.05224609 0.05761719 0.08837891
  0.07226562 0.0546875  0.03710938 0.02001953 0.02929688 0.03857422
  0.04101562 0.03955078 0.05566406 0.05371094 0.06396484 0.07177734
  0.07373047 0.08398438 0.08984375 0.08984375 0.07470703 0.06445312
  0.06445312 0.06542969 0.07958984 0.09423828 0.09667969 0.09912109
  0.10595703 0.10107422 0.11279297 0.11230469 0.11376953 0.15332031
  0.125      0.11328125 0.08398438 0.02441406 0.02880859 0.02246094
  0.01660156 0.01318359 0.00439453 0.02441406 0.05126953 0.07763672
  0.09814453 0.08349609 0.06689453 0.06103516 0.06689453 0.08789062
  0.09716797 0.10498047 0.10058594 0.09228516 0.09033203 0.09619141
  0.09912109 0.11376953 0.09863281 0.06640625 0.04345703 0.00878906
  0.01220703 0.02050781 0.02636719 0.03173828 0.04345703 0.04833984
  0.10253906 0.21484375 0.30517578 0.31738281 0.26660156 0.15576172
  0.04931641 0.03613281 0.04003906 0.03759766 0.04101562 0.0390625
  0.04882812 0.04980469 0.05371094 0.04101562 0.02197266 0.02099609
  0.01220703 0.01416016 0.04833984 0.07568359 0.08984375 0.11035156
  0.08105469 0.04882812 0.03662109 0.01416016 0.00390625 0.00732422
  0.00585938 0.00732422 0.00683594 0.00585938 0.02685547 0.04199219
  0.04882812 0.04980469 0.03027344 0.01416016 0.00830078 0.00341797
  0.00195312 0.00146484 0.00097656 0.00146484 0.00195312 0.00195312
  0.00146484 0.00048828 0.02441406 0.04150391 0.06982422 0.06982422
  0.05712891 0.05322266 0.03564453 0.04833984 0.05273438 0.04443359
  0.03808594 0.03320312 0.02587891 0.04296875 0.04541016 0.05712891
  0.06689453 0.07128906 0.07226562 0.06347656 0.06347656 0.04931641
  0.04638672 0.04101562 0.02783203 0.02197266 0.03955078 0.05859375
  0.08447266 0.10693359 0.09814453 0.08447266 0.07128906 0.04345703
  0.05419922 0.04931641 0.08203125 0.12207031 0.14013672 0.14746094
  0.11669922 0.09326172 0.09033203 0.08642578 0.10009766 0.09472656
  0.07568359 0.07373047 0.05664062 0.07421875 0.09423828 0.09570312
  0.10839844 0.10107422 0.08837891 0.08544922 0.06494141 0.07666016
  0.10888672 0.10351562]]

写音频

librosa.output.write_wav(path, audio, sr, norm=False)

波形图

import librosa.display
librosa.display.waveshow(audio, sr=22050, x_axis='time', offset=0.0, ax=None)

短时傅里叶变换

stft = librosa.stft(audio, n_fft=2048, hop_length=None, win_length=None, window='hann', center=True, pad_mode='reflect')
print(stft)
[[ 1.2299330e-06+0.0000000e+00j  1.0506814e-01+0.0000000e+00j
  -4.1960490e-01+0.0000000e+00j ... -7.7532902e-03+0.0000000e+00j
   6.8265116e-01+0.0000000e+00j  2.5062656e-01+0.0000000e+00j]
 [ 1.2116634e-06+1.7525889e-23j  3.7851952e-02+9.9753201e-02j
  -4.8766032e-01-5.7323200e-01j ...  4.9414289e-01+7.5943762e-01j
  -9.8672646e-01-7.1733482e-02j  1.4904311e-01-3.7992099e-01j]
 [ 1.1574750e-06+2.6443930e-23j -8.1521720e-02+7.5102739e-02j
   7.9587466e-01-5.3471261e-01j ... -1.0043772e+00-8.9798474e-01j
   9.2025787e-01+5.3773731e-01j -4.0258810e-01-1.1422005e-01j]
 ...
 [-7.8707920e-09+2.8149990e-23j  3.4482480e-04+3.2773399e-04j
  -3.7659094e-05-4.3389451e-04j ... -4.3171973e-04-9.3693066e-05j
   5.1885704e-04-1.2168176e-03j -2.3484134e-05+1.3648263e-03j]
 [-9.7434194e-09+2.4660322e-23j -1.7785130e-04+4.4440478e-04j
   9.9102547e-04+1.9027578e-03j ...  1.2200466e-05-9.6123083e-05j
   3.9256434e-04+4.6544659e-04j  2.9129186e-04-9.4825303e-04j]
 [-1.0377936e-08+0.0000000e+00j -4.7931357e-04+0.0000000e+00j
  -2.9597010e-03+0.0000000e+00j ... -1.9084287e-04+0.0000000e+00j
  -5.5070681e-04+0.0000000e+00j -9.8630306e-05+0.0000000e+00j]]
print(stft.shape)
# (1025, 206)
# (n_fft // 2 + 1, n_frame_num)

短时傅里叶逆变换

istft = librosa.istft(stft_matrix=stft, hop_length=None, win_length=None,window='hann', center=True,length=None)
print(istft) # waveform
print(istft.shape)

绘制频谱图
功率频谱图

import numpy as np
S = np.abs(stft)
librosa.display.specshow(S ** 2, sr=sr, y_axis='log')		# 功率频谱图
librosa.display.specshow(librosa.power_to_db(S ** 2, ref=np.max), sr=sr, y_axis='log', x_axis='time')		# 对数功率频谱图

根据频率参数获取梅尔滤波器组

melfbank = librosa.filters.mel(sr=22050, n_fft=2048, n_mels=80, fmin=2.0, fmax=8000, htk=False, norm=1)
librosa.display.specshow(melfbank, x_axis='linear')

梅尔频谱图

mel = librosa.feature.melspectrogram(y=audio, sr=sr)				# 从音频获取梅尔频谱图
librosa.display.specshow(librosa.power_to_db(mel, ref=np.max))		# 对数梅尔频谱图
D = np.abs(librosa.stft(audio)) ** 2								# 从音频做短时傅里叶变换，获取能量谱
mel = librosa.feature.melspectrogram(S=D)							# 从能量谱获取梅尔频谱图
librosa.display.specshow(librosa.power_to_db(mel, ref=np.max))		# 对数梅尔频谱图

获取MFCC

mfccs = librosa.feature.mfcc(y=audio, sr=sr, S=None, n_mfcc=20, dct_type=2, norm='ortho')
print(mfccs.shape)
# (20, 206)

torchaudio

加载音频

import torchaudio
audio, sr = torchaudio.load(path)
print(audio)
# tensor([[ 0.0000e+00,  0.0000e+00,  0.0000e+00,  ..., -3.0518e-05,
#          -6.1035e-05, -3.0518e-05]])
print(sr)
# 22050

波形图

import matplotlib.pyplot as plt
plt.figure()
plt.plot(audio.t().numpy())

重采样

transformed = torchaudio.transforms.Resample(sample_rate, new_sample_rate)(audio[channel,:].view(1,-1))

音频变换

# 频谱图
specgram = torchaudio.transforms.Spectrogram()(audio)
# 梅尔频谱图
specgram = torchaudio.transforms.MelSpectrogram()(audio)
# fbank
fbank = torchaudio.compliance.kaldi.fbank(audio, **params)

ffmpeg

多媒体处理程序，需要在本地安装二进制程序。使用它可以完成音频格式转换、采样率变换、通道变换等。以下为使用它进行音频变换的一个例子：

cmder = "-f wav -ac 1 -ar 22050"
audio_file = "1.wav"
tmp_file = "1_tmp.wav"
mpy_obj = mpy(
    executable="/usr/bin/ffmpeg",
    inputs={
        audio_file: None
    },
    outputs={
        tmp_file: cmder
    }
)
mpy_obj.run()

---

1. 参考资料：https://www.cnblogs.com/LXP-Never/p/10918590.html ↩︎

2. 参考资料：https://blog.csdn.net/weixin_30437337/article/details/96827127 ↩︎