[论文笔记|特征匹配]AdaLAM: Revisiting Handcrafted Outlier Detection

在本文中，提出了一个基于局部仿射运动验证和样本自适应阈值的离群值剔除层次结构，并将该方法命名为自适应局部仿射匹配（AdaLAM）。我们设计AdaLAM来有效利用现代并行硬件，在现代GPU上，每个图像对花费不到20毫秒的时间来从每个图像8000个关键点中生成过滤后的匹配项。

贡献：

1. 我们提出AdaLAM，这是一种新颖的离群滤波器，它从空间匹配中的一些过去想法构建为一种用于图像对应关系的快速空间验证的连贯，健壮和高度并行的算法。
2. 由于框架基于在不同情况下可能具有不同判别力的几何假设，因此提出了一种新颖的方法，该方法可以自适应地放宽我们的假设，以更好地泛化到不同的域，同时仍然挖掘每个图像区域可用的尽可能多的信息。
3. 通过实验表明，我们的自适应relaxation可提高泛化能力，并且AdaLAM可以大大胜过当前的最新方法。

图1. AdaLAM中的主要步骤，从左到右：1.我们以广泛的推设匹配项（黄色）作为输入，2.我们选择粗略区域对应关系的良好分布假设（蓝色圆圈），3.每个区域，我们认为所有推设匹配的集合均与同一区域对应假设一致。4. 我们仅保留在充分支持下与仿射变换保持局部一致的对应关系（绿色）。

1. Hierarchical Adaptive Affine Verification

给定分别在图像$I_1$和$I_2$中的关键点$K_1$和$K_2$的集合，我们将所有假定匹配的集合$M$视为从$K_1$到$K_2$的最近邻居匹配的集合。实际上，由于描述子的限制，$M$被绝大多数不正确的匹配所影响，因此我们的目标是产生一个子集$M^{\prime }\subseteq M$(是所有集合最接近的可能的近似值)和唯一正确的内点匹配集合$M^{\ast }\subseteq M$。

我们的方法建立在经典空间匹配方法的基础上。 为了降低计算成本，我们将匹配搜索限制为描述子空间中最接近的邻居的初始假定匹配集合$M$。 图1展示了算法的主要步骤，总结如下：

1.找到初始匹配（最近邻top1）：

我们为每个匹配赋值一个score（score可以从ratio test得 到，置信度越高score越高），然后使用非极大值抑制得到score最高的match point即选取为seed点；

2、选取满足条件的种子点的附近的点（匹配），构成邻域来支持seed点。

3、每个邻域集合中使用固定迭代次数的ransac，保留那些局部一致较好匹配；

4、并行计算所有的seed点，得到整体的匹配对，根据一定阈值做整体的迭代。

1.1 Seed points selection

对于种子点的选择，我们为每个关键点分配一个置信度分数，然后如果关键点在半径R内具有最高分数，则将该关键点作为种子点。作为置信度分数，我们使用适用于关键点的最近邻匹配的$比值检验$。 由于每个匹配点都是独立的，此时可用GPU对该过程进行并行加速。

这样可以确保种子点的独特性和覆盖范围，而不会引起网格伪影，同时使选择完全平行以在GPU上进行高效计算，因为可以对每个对应关系进行评分并与邻居进行比较，以独立于其他选择的最终选择。

1.2 Local neighborhood selection and filtering

将对应关系分配给种子点是算法中的关键步骤，因为它围绕P的每个假设建立了搜索空间以找到仿射变换A。更宽的邻域可以更容易地包含正确的对应关系以适合A，而同时它们隐式放宽仿射约束，因为它们违反了局部性假设。

令$S_i=(x_1^{S_i},x_2^{S_i})$为种子点匹配关系，从其局部特征帧中产生相似性转换$({\alpha }^{S_i}={\alpha }_2^{S_i}-{\alpha }_1^{S_i},{\sigma }^{S_i}={\sigma }_2^{S_i}/{\sigma }_1^{S_i})$，并分解为方向分量${\alpha }^{S_i}$和尺度分量${\sigma }^{S_i}$ ,$N_i\subseteq M$是分配给$S_i$的一组对应关系，以验证仿射一致性。 令$t_{\alpha }$和$t_{\sigma }$为候选匹配和种子匹配$S_i$之间的方向和尺度一致的阈值。 匹配关系$(p_1,p_2)=((x_1,d_1,{\sigma }_1,{\alpha }_1),(x_2,d_2,{\sigma }_2,{\alpha }_2))\in M$如果满足以下约束，它将$({\alpha }^p={\alpha }_2-{\alpha }_1,{\sigma }^p={\sigma }_2/{\sigma }_1)$分配给$N_i$：

其中$R_1$和$R_2$是分别用于在图像$I_1$和$I_2$中传播种子点的半径；$\lambda$是一个超参数，可调节邻域之间的重叠。请注意，我们考虑以2π取模的角度$\alpha$位于区间(-π，π]之内。选择与图像区域成比例的不同半径$R_1$和$R_2$，以使图像缩放保持不变。

从式(1),我们在$N_i$中包含所有在$\lambda R$半径内的两个图像中局部一致的$M$中的所有对应关系，即与种子匹配大致在相同区域匹配的所有对应关系。 根据式(2),我们进一步过滤$N_i$，以确保包含的对应关系在独立阈值$t_{\alpha }$和$t_{\sigma }$内引起与$({\alpha }^{S_i},{\sigma }^{S_i})$一致的相似度变换$({\alpha }^p,{\sigma }^p)$。在此阶段，可以对每个集合$N_i$进行独立处理，进行仿射验证。

独立的阈值编码对关键点提供的方向和尺度信息可靠性的置信度。 使用方向和尺度一致性进行验证的想法已经被反复提出来作为离群值剔除的指示。

1.3 Adaptive Affine Verification

-如何在相邻集合$N_i$中选择inliers?

-在每个邻域集合$N_i$中使用固定迭代次数的ransac，得到得分最高的内点集合。

在每次迭代$j$时，我们对一个最小集合进行采样，并为每个相邻集合$N_i$拟合仿射变换$A_i^j$。 将残差$r_k$分配给点$x_1^k$,$x_2^k$的对应关系$k$，以测量其与$A_i^j$的偏差：

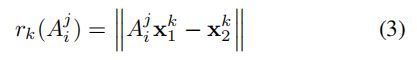
如3.1节所述，仿射模型只是部分解释了我们想要识别的图像运动，与仿射模型的误差没有明显的约束。因此，我们不能对$r_k$设置一个固定的阈值来确定$k$是否为inlier。

如果$H_o$是具有均匀分散的离群值对应关系的假设，我们将残差集合$R$中的残差值$r_k$映射到置信度$c_k$：

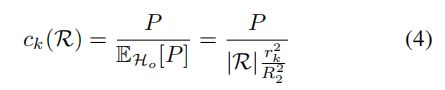
其中，正样本计数$P=|l:r_l\le r_k|$是假设对应$k$是最差inlier时inliers的数量。所提出的置信度$c$有效地衡量了实际发现的inliers数量与仅异常值假设$H_o$下将被发现的inliers数量之间的比率。

我们并行计算每一次迭代的所有样本的置信度，并在置信度上选择具有固定阈值$t_c$的inliers。最后，对于每个集合$N_i$，我们只输出获得最高inlier计数的inliers，并进一步过滤得分小于$t_n$ 的inliers以获得最佳迭代。

2. 实验结果