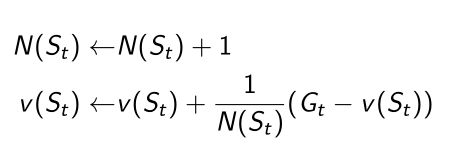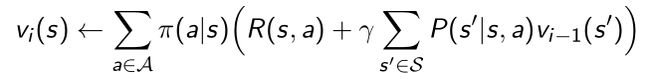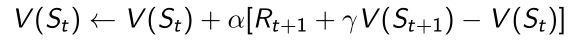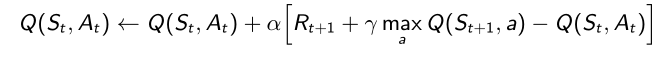【强化学习纲要】3 无模型的价值函数估计和控制
【强化学习纲要】3 无模型的价值函数估计和控制
-
- 3.1 回顾MDP的控制
- 3.2 Model-free prediction
-
- 3.2.1 Monte Carlo policy evaluation
- 3.2.2 Temporal Difference (TD) learning
- 3.3 Model-free control
-
- 3.3.1 Sarsa: On-Policy TD Control
- 3.3.2 On-policy Learning vs. Off-policy Learning
- 3.3.3 Off-policy Control with Q-Learning
- 3.3.4 Sarsa与Q-Learning的比较
- 3.3.5 Sarsa and Q-learning Example
周博磊《强化学习纲要》
学习笔记
课程资料参见:https://github.com/zhoubolei/introRL.
教材:Sutton and Barton
《Reinforcement Learning: An Introduction》
实际生活中,很多MDP是不可知的,因此要使用Model-free的方法。
3.1 回顾MDP的控制
- 什么时候MDP已知?
- 马尔科夫决策过程中 R R R和 P P P都是暴露给agent的
- 因此agent可以通过policy iteration和value iteration来寻找最佳策略
- Policy iteration
- Value iteration
利用Bellman optimality backup来更新价值函数,当把max操作运行很多很多次以后会得到每一个策略的价值函数
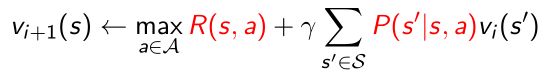
利用policy retrieve来更新最终的策略
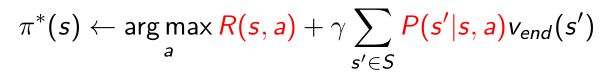
3.2 Model-free prediction
- 但是很多MDP是未知的,或者太复杂。因此我们需要用Model-free RL,Model-free 就是典型的agent与环境交互获得观测和奖励来调整它的行为,通过一系列的观测收集到的数据来调整它的策略。

- 并没有直接获得转移状态和奖励函数
- 通过agent与环境进行交互,采集到了很多轨迹数据
- 轨迹表现为:

- 在不能获取MDP model的情况下估计expected return
- Monte Carlo policy evaluation(蒙特卡洛)
- Temporal Difference (TD) learning
3.2.1 Monte Carlo policy evaluation
-
MC simulation:在算取每个轨迹实际的return后,把很多轨迹进行平均,得到每个状态下面对应的价值。
-
MC policy evaluation是根据empirical mean return来估计,而不是expected return
-
因此并不需要MDP的转移函数和奖励函数,也不要像动态规划一样有bootstrapping的过程。
-
只能用于有终止的MDP
-
算法概括
当要估计某个状态的时候,从这个状态开始通过数数的办法,数这个状态被访问了多少次,从这个状态开始我们总共得到了多少的return,最后再取empirical mean,就会得到每个状态的价值。

通过大数定律,得到足够的轨迹后,就可以趋近策略对应得价值函数
![]()
- Incremental Mean
通过采样很多次,就可以平均;然后进行分解,把加和分解成最新的 x t x_t xt的值和最开始到t-1的值;然后把上一个时刻的平均值也带入进去,分解成(t-1)乘以上一个时刻的平均值;这样就可以把上一个时刻的平均值和这一个时刻的平均值建立一个联系。
通过这种方法,当得到一个新的 x t x_t xt的时候,和上一个平均值进行相减,把这个差值作为一个残差乘以一个learning rate,加到当前的平均值就会更新我们的现在的值。这样就可以把上一时刻的值和这一时刻更新的值建立一个联系。
- Incremental(增量) MC Updates
把蒙特卡洛方法也写成Incremental MC更新的方法。
-
将 1 / c o u n t i n g 1/counting 1/counting变成 α \alpha α,也叫learning rate(学习率),我们希望值更新的速率有多快
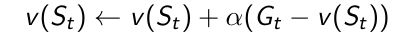
-
MC与DP的差异
-
DP(动态规划)
-
MC(蒙特卡洛)
MC表现出来得到的是这条从起始到终止的蓝色的轨迹,我们得到的是一条实际的轨迹,每一个采取的什么行为以及它到达的状态都是决定的。现在是只是利用得到的实际价值来更新在轨迹上的所有状态,而和轨迹没有关系的状态我们都没有更新
-
MC相对于DP的好处
- MC可以在环境不知道的情况下进行工作,是model-free状态。
- MC每次只需要更新一条轨迹,和轨迹不相关的是不需要更新的,极大的减少了更新的成本;DP是算了两次加和,需要把MDP里面所有状态都迭代一边才能更新,如果样本数量太大,就会非常慢。
3.2.2 Temporal Difference (TD) learning
- TD是介于MC和DP之间的方法
- TD是model-free的,不需要知道MDP的转移矩阵或奖励函数
- TD结合了bootstrapping的思想,对于不完整的episode也可以工作。
算法框架
- 目标:在policy π \pi π中在线学习 v π v_{\pi} vπ
- 最简单的TD算法(TD(0))算法:
- 每次往前走一步,bootstrapping得到的estimated return来更新上一时刻的状态 v ( S t ) v_(S_t) v(St)的值
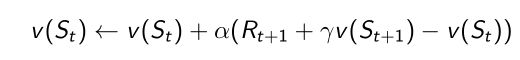
- estimated return也叫TD target:

由两部分组成,第一部分表示走了某一步过后得到的奖励,第二部分是通过bootstrapping找到 v ( S t + 1 ) v_(S_{t+1}) v(St+1),再乘以一个折扣系数。 - TD error:
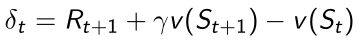
TD target减去当前的v值 - 与Incremental MC对比

G i , t G_{i,t} Gi,t是实际得到的值,一条轨迹跑完了后算每个状态实际的return,TD是没有等轨迹结束,在往前走了一步后就可以更新它的价值函数
- 每次往前走一步,bootstrapping得到的estimated return来更新上一时刻的状态 v ( S t ) v_(S_t) v(St)的值
TD和MC的差别
TD是在决策树上只走了一步,MC是把整个决策树全部走完了,走到终止状态后,回算每个return,更新它的值。

- TD可以通过online learning,每完成一步更新一步,效率高;MC需要等到整个序列完成后才可以学习。
- TD可以学习不完整的序列,MC要学习完成的序列。
- TD可以在连续(没有终止)的环境下面进行学习;MC必须在有终止的情况下学习。
- TD利用了Markov特征,在Markov环境下效率更高;MC并没有这个假设,当前状态与之前状态是没有关系的,是用最终实际的奖励来估计中间每一个状态的价值。
n-step TD
- TD(0)是从当前状态走到下一个状态,走了一步。通过调整这个步数,可以得到不同的步数的算法,比如两步TD算法,就是向前走两步,然后最前面那个state进行bootstrapping,然后根据两步得到的实际奖励来更新它的值。
- 这样就可以通过调整步数来调整究竟需要多少的实际奖励以及多少bootstrapping,这也是TD比较灵活的地方。
- 当步数增加到很多(infinite)的时候,整个TD target就变成了MC target
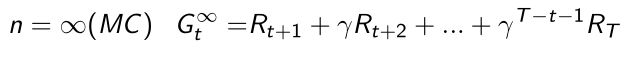
- 可以把n- step return再定义成
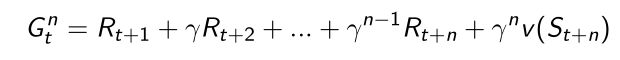
当走到它最前面的一个state的时候,利用 v ( S t + n ) v(S_{t+n}) v(St+n)来bootstrapping来回到return

- 然后利用incremental learning的方法来更新state的价值
Bootstrapping and Sampling for DP, MC, and TD
- Bootstrapping
- MC没有用到之前的bootstrap,它没有用到任何之前的估计
- DP用了bootstrap
- TD用来bootstrap
- Sampling
- MC是纯sampling的办法
- DP没有sampling
- TD用了sampling,它的TD target一部分是sampling,一部分是bootstrap
可视化展示
- DP backup

直接算expectation,直接算某状态相关联的未来一步的状态,加和起来,如图红色区域。 - MC backup
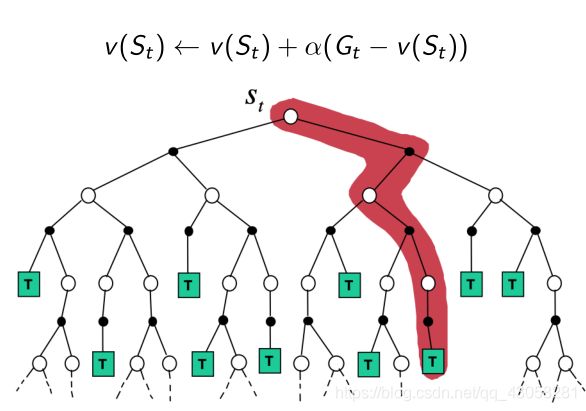
直接找一个状态开始的一条轨迹,在这条轨迹上更新所有状态。 - TD backup

把当前状态开始往前走一步,关注的只是很局部的一个步骤。

3.3 Model-free control
- 在没法的到MDP模型的情况下,如何优化价值函数,如何得到最佳的策略呢?
- Generalized Policy Iteration(GPI),把policy iteration进行广义的推广使得它能够兼容MC和TD。
Policy iteration
两部分:
- 迭代的过程估计价值函数 v v v
- 得到价值函数后,通过greedy的算法改进
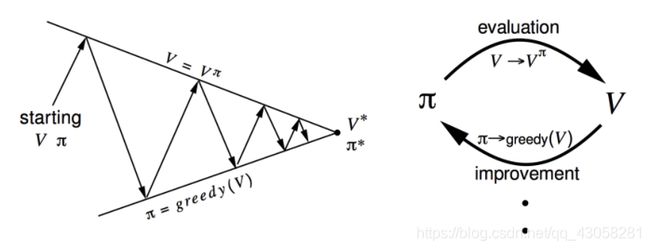
然而得到了价值函数后,我们并不知道它的奖励函数和状态转移,所以没法估计q函数。

所以当我们不知道奖励函数和状态转移矩阵的时候,如何进行策略的优化?
Generalized Policy Iteration with Action-Value Function
可以直接用MC的方法代替DP的方法去估计q函数,当得到q函数后,可以通过greedy的方法去改进。
- 假设每个episode都有一个exploring starts, exploring starts意味着希望每个状态每个步骤都采样到,所以需要episode start作为保证。
通过蒙特卡洛采样的方法采集到很多轨迹,每个轨迹都可算得它的价值;然后通过average的方法去估计q函数,可以把q函数看成一个table,横轴是状态,纵轴是action,通过采样的方法把表格上面每一个值都填上;得到表格后,可以通过第二步得policy improvement选取它的更好的一个策略。
核心:如何利用MC方法去填Q table。
怎么确保MC有足够的贪婪函数?
- 面临一个exploration和exploitation的trade-off
- ϵ \epsilon ϵ-Greedy exploration:
在每一步选取策略的时候,有 ϵ \epsilon ϵ的概率, ϵ \epsilon ϵ在开始的时候是比较大的,比如80%,逐渐它会减小。
Monte Carlo with ϵ \epsilon ϵ-Greedy Exploration
当我们follow ϵ \epsilon ϵ -greedy policy的时候,整个q函数以及价值函数是单调递增的。

ϵ \epsilon ϵ-Greedy算法表示

注释:
1:刚开始时q table是随机初始化的;
4: MC的核心是利用当前的策略利用环境进行探索,得到一些轨迹;
7:得到轨迹后,开始更新return,通过incremental mean的方法更新q table, q table有两个量:状态,action;
10:得到q table后,进步更新策略,policy improvement,这样就可以得到下一阶段的策略;得到更好的策略后,又用更好的策略来进行数据的采集。
这样通过迭代的过程,就得到广义的policy iteration。
MC vs. TD for Prediction and Control
- TD的好处
- 变化性低
- Online(对于没有结束的游戏已经可以处理它的q table)
- 不完整的序列
- 把TD放到control loop里面
- 估计它的q table
- 采取 ϵ \epsilon ϵ-Greedy improvement的方式
- 在同一个episode没有结束的时候就可以更新它没有采集的状态
回顾TD prediction的步骤
- TD prediction给定了一个策略,我们估计它的价值函数
- TD(0)的方法是
- 那么怎么用TD prediction来估计action value function Q(S)呢?
3.3.1 Sarsa: On-Policy TD Control
On-Policy的意思是我们现在只有同一个policy,既利用这个policy来采集数据,policy同时也是我们优化的policy。
- 需要采集到两个state。从当前S开始,执行了一个action(第一个A),会得到一个reward,然后会进入下一个状态S;然后进一步执行action,得到第二个A…,缩写得到Sarsa
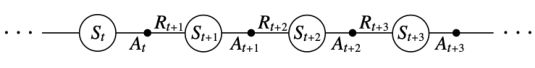
- Sarsa算法与TD prediction类似,它是直接去估计Q table, Q table也是构造出TD target,由它已经得到的reward,以及bootstrapping下一步要更新的Q,来更新当前Q table的值。

- 得到Q table后,可以采取greedy的策略更新它的策略。
Sarsa具体的算法

刚开始我们初始化Q table;先通过Q table采样一个A;采取A,会得到奖励R和S‘(进入到下一个状态);再一次通过Q table采样得到A’;收集到所有data后,就可以更新Q table;更新后我们会向前走一步,S变成S’,A变成A’;一步一步进行迭代更新。
n-step Sarsa
前面我们说可以把TD算法扩展它的步数,我们可以得到n-step 的Sarsa。
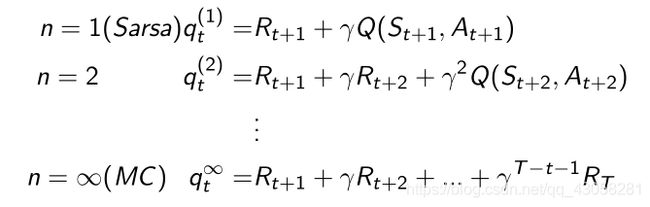
一步Sarsa是往前走一步过后就更新它的TD target;两步就得到两个实际得到的奖励,再bootstrapping Q的价值,更新TD target;进一步推广到整个结束过后,Sarsa就变成MC的这种更新的方法。
3.3.2 On-policy Learning vs. Off-policy Learning
Sarsa属于On-policy Learning
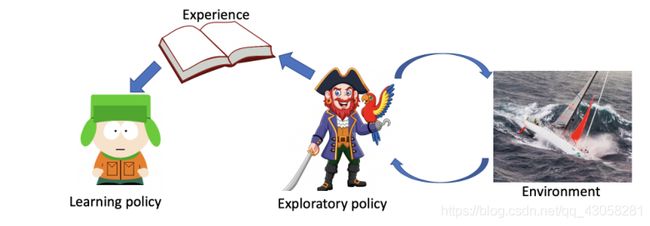
- On-policy Learning:因为需要学到最新(最佳)的策略 π \pi π,但在学习的过程中只利用一种策略,既利用这个策略进行数据(轨迹)的采集,也进一步进行策略的优化,都是用的同一个策略。
- Off-policy Learning:在策略的学习过程中,可以保留两种不同的策略。一种是保持优化的策略,我们希望学到最佳的策略;另一种是拿来探索的策略,可以更激进的对环境探索。我们需要学习策略policy π \pi π,但我们利用的数据(轨迹)是用第二个策略 μ \mu μ产生的。
- π \pi π: target policy,需要学习的policy;
- μ \mu μ:behavior policy,采集数据,然后喂给 target policy进行学习。
Off-policy Learning
- 在behavior policy μ ( a ∣ s ) \mu(a|s) μ(a∣s)中收集data的时候
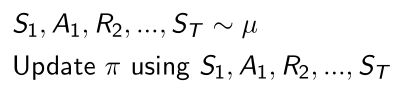
- 观测,轨迹等都是通过 μ \mu μ与环境进行交互产生的
- 然后去update π \pi π policy
- Off-policy Learning 好处
- 利用一个更加激进的exploratory policy,学到一个最佳的策略,使得学习效率非常高
- 可以学习其他agent的行为,如模仿学习
- 可以重用之前老的策略产生的轨迹。探索的过程需要消耗非常多的计算资源来产生roll out,产生轨迹;如果我们之前产生的轨迹对于当前产生的轨迹不能利用的话,会浪费很多资源。 这也是Q learning, Deep Q learning采取的思想;用一个replay buffer来存储老的轨迹生的经验,然后通过对这些老的策略进行采样,来构建新的training back来更新target policy。
3.3.3 Off-policy Control with Q-Learning
- behavior and target policy
- target policy π \pi π直接在Q table上greedy

对于某一个状态,下一步的最佳策略应该是argmax操作取得下一个能得到的所有状态。 - behavior policy μ \mu μ可以是随机的policy,但是这里是让它在Q table上遵循 ϵ \epsilon ϵ-Greedy policy
- 这两种policy在策略优化的开始是非常不同的,因为 ϵ \epsilon ϵ-Greedy的 ϵ \epsilon ϵ值在刚开始的时候是非常大的;在逐渐收敛的时候, ϵ \epsilon ϵ的值也会逐渐变小;因此这两个策略在后面会越来越像。
- Q-learning target:
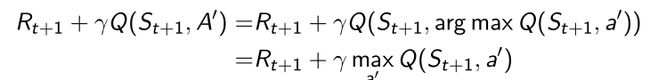
每一步后面采取的策略都应该是argmax操作,变换知乎直接取的max值。所以就构建出当前TD target要优化的值。 - 把Q-learning update写成incremental的形式

Q-learning 算法
- 我们采取当前行为过后,然后用 ϵ \epsilon ϵ-Greedy选择A,得到R,S’。
- 与Sarsa很大的不同的是,Q-learning 算法并没有采样第二个Action,因为第二个Action是需要构造TD target的,所以在Sarsa中需要遵从target policy去采样第二个A;
- 在Q-learning并没有去采样,采取的操作是直接去看Q table,然后取它的max值,这样就构造出了它的TD target,然后就可以对它的Q值进行优化,优化后就进入下一步的S状态。
3.3.4 Sarsa与Q-Learning的比较
- Sarsa: On-Policy TD control
- Q-Learning: Off-Policy TD control
- Backup diagram for Sarsa and Q-learning

- Sarsa只有一条路,通过当前S采样出A得到奖励R,然后到达S’,再采样target policy得到A’,就可以更新了。A和A’都是同一个policy产生的,是on-policy。
- Q-learning有了S,A采样过后有了reward,然后得到S’,接着有一个max operator的操作,当前的max operator作为下一步最可能的action。A和A’是从不同的policy产生的,是off-policy。
Example on Cliff Walk
https://github.com/cuhkrlcourse/RLexample/blob/master/modelfree/cliffwalk.py
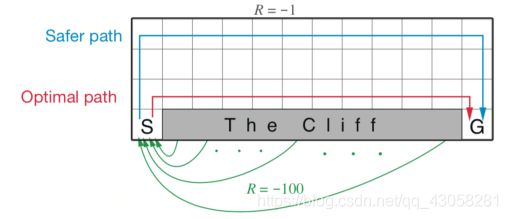
- agent需要从S格子到G格子,可以上下左右移动,但是要避免cliff格子,如果走到cliff有-100的奖励;每走一步有一个-1的奖励。

- Sarsa得到的结果(最佳轨迹)与Q-learning非常不同,因为Sarsa是on-policy learning,因为如果掉到cliff就会得到很负的奖励,所以它会采取非常保守的策略。
- R是走的轨迹,Sarsa的会逐渐往上走,这样使得agent尽量远离cliff的位置;Q-learning会非常激进,沿着悬崖边上走,得到最优的策略。
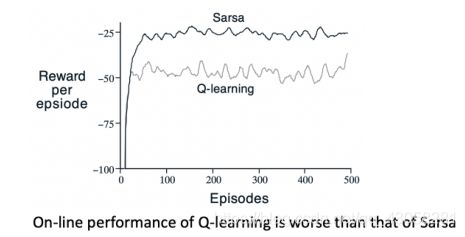
- Q-learning的learning curve相对于Sarsa是更低的,因为它采取的policy非常激进,有一个behavior policy随机探索环境,所以有更大的概率掉到cliff。
DP和TD的总结
3.3.5 Sarsa and Q-learning Example
https://github.com/cuhkrlcourse/RLexample/tree/master/modelfree
cliffwalk.py
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import hsv_to_rgb
def change_range(values, vmin=0, vmax=1):
start_zero = values - np.min(values)
return (start_zero / (np.max(start_zero) + 1e-7)) * (vmax - vmin) + vmin
class GridWorld:
terrain_color = dict(normal=[127/360, 0, 96/100],
objective=[26/360, 100/100, 100/100],
cliff=[247/360, 92/100, 70/100],
player=[344/360, 93/100, 100/100])
def __init__(self):
self.player = None
self._create_grid()
self._draw_grid()
self.num_steps = 0
def _create_grid(self, initial_grid=None):
self.grid = self.terrain_color['normal'] * np.ones((4, 12, 3))
self._add_objectives(self.grid)
def _add_objectives(self, grid):
grid[-1, 1:11] = self.terrain_color['cliff']
grid[-1, -1] = self.terrain_color['objective']
def _draw_grid(self):
self.fig, self.ax = plt.subplots(figsize=(12, 4))
self.ax.grid(which='minor')
self.q_texts = [self.ax.text(*self._id_to_position(i)[::-1], '0',
fontsize=11, verticalalignment='center',
horizontalalignment='center') for i in range(12 * 4)]
self.im = self.ax.imshow(hsv_to_rgb(self.grid), cmap='terrain',
interpolation='nearest', vmin=0, vmax=1)
self.ax.set_xticks(np.arange(12))
self.ax.set_xticks(np.arange(12) - 0.5, minor=True)
self.ax.set_yticks(np.arange(4))
self.ax.set_yticks(np.arange(4) - 0.5, minor=True)
def reset(self):
self.player = (3, 0)
self.num_steps = 0
return self._position_to_id(self.player)
def step(self, action):
# Possible actions
if action == 0 and self.player[0] > 0:
self.player = (self.player[0] - 1, self.player[1])
if action == 1 and self.player[0] < 3:
self.player = (self.player[0] + 1, self.player[1])
if action == 2 and self.player[1] < 11:
self.player = (self.player[0], self.player[1] + 1)
if action == 3 and self.player[1] > 0:
self.player = (self.player[0], self.player[1] - 1)
self.num_steps = self.num_steps + 1
# Rules
if all(self.grid[self.player] == self.terrain_color['cliff']):
reward = -100
done = True
elif all(self.grid[self.player] == self.terrain_color['objective']):
reward = 0
done = True
else:
reward = -1
done = False
return self._position_to_id(self.player), reward, done
def _position_to_id(self, pos):
''' Maps a position in x,y coordinates to a unique ID '''
return pos[0] * 12 + pos[1]
def _id_to_position(self, idx):
return (idx // 12), (idx % 12)
def render(self, q_values=None, action=None, max_q=False, colorize_q=False):
assert self.player is not None, 'You first need to call .reset()'
if colorize_q:
assert q_values is not None, 'q_values must not be None for using colorize_q'
grid = self.terrain_color['normal'] * np.ones((4, 12, 3))
values = change_range(np.max(q_values, -1)).reshape(4, 12)
grid[:, :, 1] = values
self._add_objectives(grid)
else:
grid = self.grid.copy()
grid[self.player] = self.terrain_color['player']
self.im.set_data(hsv_to_rgb(grid))
if q_values is not None:
xs = np.repeat(np.arange(12), 4)
ys = np.tile(np.arange(4), 12)
for i, text in enumerate(self.q_texts):
if max_q:
q = max(q_values[i])
txt = '{:.2f}'.format(q)
text.set_text(txt)
else:
actions = ['U', 'D', 'R', 'L']
txt = '\n'.join(['{}: {:.2f}'.format(k, q) for k, q in zip(actions, q_values[i])])
text.set_text(txt)
if action is not None:
self.ax.set_title(action, color='r', weight='bold', fontsize=32)
plt.pause(0.01)
def egreedy_policy(q_values, state, epsilon=0.1):
'''
Choose an action based on a epsilon greedy policy.
A random action is selected with epsilon probability, else select the best action.
'''
if np.random.random() < epsilon:
return np.random.choice(4)
else:
return np.argmax(q_values[state])
def q_learning(env, num_episodes=500, render=True, exploration_rate=0.1,
learning_rate=0.5, gamma=0.9):
q_values = np.zeros((num_states, num_actions))
ep_rewards = []
for _ in range(num_episodes):
state = env.reset()
done = False
reward_sum = 0
while not done:
# Choose action
#第一个action, $\epsilon$-Greedy产生的
action = egreedy_policy(q_values, state, exploration_rate)
# Do the action
#往前走了一步
next_state, reward, done = env.step(action)
reward_sum += reward
# Update q_values
#可以通过bootstrapping去看max的值,构造出当前的TD target
td_target = reward + 0.9 * np.max(q_values[next_state])
td_error = td_target - q_values[state][action]
#得到TD target后可以立刻更新q value的值,并不需要执行第二个action
q_values[state][action] += learning_rate * td_error
# Update state
#进入到下一个state
state = next_state
if render:
env.render(q_values, action=actions[action], colorize_q=True)
ep_rewards.append(reward_sum)
return ep_rewards, q_values
def sarsa(env, num_episodes=500, render=True, exploration_rate=0.1,
learning_rate=0.5, gamma=0.9):
q_values_sarsa = np.zeros((num_states, num_actions))
ep_rewards = []
for _ in range(num_episodes):
state = env.reset()
done = False
reward_sum = 0
# Choose action
#第一个action
action = egreedy_policy(q_values_sarsa, state, exploration_rate)
while not done:
# Do the action
next_state, reward, done = env.step(action)
reward_sum += reward
# Choose next action
#第二个action,通过采样得到
next_action = egreedy_policy(q_values_sarsa, next_state, exploration_rate)
# Next q value is the value of the next action
#构造TD target
td_target = reward + gamma * q_values_sarsa[next_state][next_action]
#计算TD error
td_error = td_target - q_values_sarsa[state][action]
# Update q value
#对Q值进行更新
q_values_sarsa[state][action] += learning_rate * td_error
# Update state and action
state = next_state
action = next_action
if render:
env.render(q_values, action=actions[action], colorize_q=True)
ep_rewards.append(reward_sum)
return ep_rewards, q_values_sarsa
def play(q_values):
# simulate the environent using the learned Q values
env = GridWorld()
state = env.reset()
done = False
while not done:
# Select action
action = egreedy_policy(q_values, state, 0.0)
# Do the action
next_state, reward, done = env.step(action)
# Update state and action
state = next_state
env.render(q_values=q_values, action=actions[action], colorize_q=True)
UP = 0
DOWN = 1
RIGHT = 2
LEFT = 3
actions = ['UP', 'DOWN', 'RIGHT', 'LEFT']
### Define the environment
env = GridWorld()
num_states = 4 * 12 #The number of states in simply the number of "squares" in our grid world, in this case 4 * 12
num_actions = 4 # We have 4 possible actions, up, down, right and left
### Q-learning for cliff walk
q_learning_rewards, q_values = q_learning(env, gamma=0.9, learning_rate=1, render=False)
env.render(q_values, colorize_q=True)
q_learning_rewards, _ = zip(*[q_learning(env, render=False, exploration_rate=0.1,
learning_rate=1) for _ in range(10)])
avg_rewards = np.mean(q_learning_rewards, axis=0)
mean_reward = [np.mean(avg_rewards)] * len(avg_rewards)
fig, ax = plt.subplots()
ax.set_xlabel('Episodes using Q-learning')
ax.set_ylabel('Rewards')
ax.plot(avg_rewards)
ax.plot(mean_reward, 'g--')
print('Mean Reward using Q-Learning: {}'.format(mean_reward[0]))
### Sarsa learning for cliff walk
sarsa_rewards, q_values_sarsa = sarsa(env, render=False, learning_rate=0.5, gamma=0.99)
sarsa_rewards, _ = zip(*[sarsa(env, render=False, exploration_rate=0.2) for _ in range(10)])
avg_rewards = np.mean(sarsa_rewards, axis=0)
mean_reward = [np.mean(avg_rewards)] * len(avg_rewards)
fig, ax = plt.subplots()
ax.set_xlabel('Episodes using Sarsa')
ax.set_ylabel('Rewards')
ax.plot(avg_rewards)
ax.plot(mean_reward, 'g--')
print('Mean Reward using Sarsa: {}'.format(mean_reward[0]))
# visualize the episode in inference for Q-learing and Sarsa-learning
play(q_values)
play(q_values_sarsa)