FFT算法实现(fft算法)--快速傅里叶变换算法实现

本文作者：韩申权
作者博客：http://www.cnblogs.com/hsqdboke
转载请注明出处，侵权必究，保留最终解释权！

首先先要理解离散傅里叶变换(DAT)，然后再理解其快速计算方法(FFT)的原理，和蝴蝶算法的内涵，否则将写不出代码；

蝴蝶算法内涵：

(WN)^n的计算：

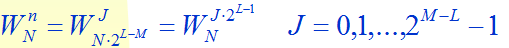
本代码为频率基2抽取算法，也许只看上面这些内容也不一定能懂得FFT算法，不过多查些资料就可以了！

//快速傅里叶变换(FFT) 只看课本是看不会的,介绍的太笼统...

#include<iostream>

#include<math.h>

#include<string.h>

#define PI 3.14159

using namespace std;

double x1[100000],x2[100000],w1[100000],w2[100000];//角标1代表实数部分,2虚数部分

int visited[100000];

int s[1000];    

void wnp(int M,int L,int N) //求(WN)^p

{

    int i,k;

    int t1=(int)(pow(2.0,M-L))-1;

    double t2=-2*PI/N;

    double a,b;

    memset(w1,0,sizeof(w1));

    memset(w2,0,sizeof(w2));

    k=(int)(pow(2.0,L-1));

    a=cos(t2*k);

    b=sin(t2*k);

    w1[0]=1; //当0的情况

    w2[0]=0;

    for(i=1;i<=t1;i++)

    {

        w1[i]=a*w1[i-1]-b*w2[i-1];

        w2[i]=a*w2[i-1]+b*w1[i-1];

    }

}

void FFT(int N,int M)

{

    int i,j,n=N;

    double a,b;

    for(i=1;i<=M;i++)  //从第1级到M级

    {

        n/=2;

        memset(visited,0,sizeof(visited));//标记数组清零

        wnp(M,i,N);  //调用wnp函数    

        for(j=0;j<N;j++)   //分别求每一级的当前实数部分和虚数部分

        {

            if(!visited[j])

            {

                visited[j]=1;

                visited[j+n]=1;

                a=x1[j]-x1[j+n]; //此处曾出错 应先计算出其值 因为后面 x1[j]和x2[j]的值会改变

                b=x2[j]-x2[j+n];

                x1[j]=x1[j]+x1[j+n];

                x2[j]=x2[j]+x2[j+n];                

                

                int t=j%(N/(int)(pow(2.0,i*1.0)));

                x1[j+n]=a*w1[t]-b*w2[t];

                x2[j+n]=a*w2[t]+b*w1[t];

            }

        }    

    }

}

void solve(double *x,int N,int M) //数位倒读

{

    int a,i,j,k;

    double t;

    for(k=0;k<N/2;k++)

    {

        i=k;

        a=0;

        memset(s,0,sizeof(s));    

        for(j=0;j<M;j++)

        {

            s[j]=i%2;

            i/=2;

        }

        for(j=0;j<M;j++)

        {

            a=a+s[j]*(int)(pow(2.0,M-1-j));

        }

        t=x[a];

        x[a]=x[k];

        x[k]=t;

    }    

}

int main()

{

    //freopen("d:\\1.txt","r",stdin);

    int N,i,M;

    cout<<"请输入区段长度N(N需是2的整数次方): ";

    cin>>N;

    M=floor(log10(N*1.0)/log10(2.0)+0.5);

    cout<<"请分别输入N个采样值序列复数的实部和虚部: "<<endl;

    for(i=0;i<N;i++)

    {

        printf("实部x1[%d]=",i);

        cin>>x1[i];

        printf("虚部x2[%d]=",i);

        cin>>x2[i];

    }

    FFT(N,M);

    solve(x1,N,M);

    solve(x2,N,M);

    printf("得到的频谱值为:\n");

    for(i=0;i<N;i++)

        printf("X[%d]=(%.2lf)+(%.2lf)j\n",i,x1[i],x2[i]);

    return 0;

}

本文作者：韩申权
作者博客：http://www.cnblogs.com/hsqdboke
转载请注明出处，侵权必究，保留最终解释权！