光流估计(二) FlowNet 系列文章解读
在上篇文章中,我们学习并解了光流(Optical Flow)的一些基本概念和基本操作,但是传统的光流估计方法计算比较复杂、成本较高。近些年来随着CNN卷积神经网络的不断发展和成熟,其在各种计算机视觉任务中取得了巨大成功(多用于识别相关任务)。于是,将光流估计与CNN深度学习相结合提出了FlowNet系列文章,首次将CNN运用到光流预测上,使网络能从一对图片中预测光流场,每秒达到5到10帧率,并且准确率也达到了业界标准。
一.FlowNet
FlowNet(或称为FlowNet 1.0)是FlowNet系列所提出的第一个光流估计网络,也是最重要最基础的网络,其思想来自于论文《FlowNet: Learning Optical Flow with Convolutional Networks》,这篇文章发布在IEEE International Conference on Computer Vision (ICCV), 2015。
该文章首先提出了一种端到端的光流估计学习的神经网络结构,该网络结构总体上是一种 Encoder/Decoder 的编/解码器结构。信息首先在网络的收缩部分进行空间压缩和特征提取,然后在扩展部分进行细化。FlowNet 网络的输入是一个图像对(包含相邻两帧),以及其对应的光流 ground truth。其次,由于目前现有的光流数据集不足以训练一个大型网络,该文章还通过虚拟合成出了一个名叫Flying Chairs的有关椅子图像的数据集,在网络训练过程中得到了较好的效果。
1.网络结构
根据在编码/收缩部分网络结构的不同,文章又将 FlowNet 细分为 FlowNet-Simple(FlowNet-S) 和 FlowNet-Correlation(FlowNet-C)两种结构,二者在解码/扩展部分是一致的,我们将分别介绍如下。
1.1 Contracting part 编码/收缩部分
(1)FlowNet-S
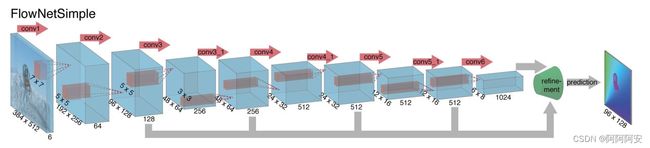
FlowNetSimple是最简单粗暴的一种网络结构,该网络直接把输入的两帧图像在通维度上堆叠(拼接)在一起,然后使用一系列卷积层进行下采样提取特征,让网络自行决定如何处理图像对以从中提取运动信息,网络结构如上图所示。
(2)FlowNet-C
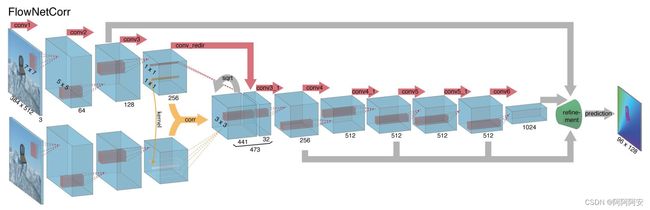
FlowNetCorrelation与FlowNet-S的区别在于,FlowNet-C首先对两个输入图像建立两个独立但相同的处理流,通过一系列的卷积层分别提取两个图像的有意义的特征表示。随后在更高的层次上将这些有意义的特征表示组合到一起进行后续的下采样过程,网络结构如图上图所示。
但是两个图象高层特征的组合并不是简单的维度堆叠,而是采用了关联层来促进网络的匹配过程。我们知道,该网络的最终目的是预测两张图像之间的光流,而光流本质上就是一种不同图像之间的对应匹配关系,为了“帮助”网络加速计算这种匹配关系、提高网络性能、提高估计的准确性,我们引入了一个"correlation layer"来组合特征。"correlation"操作就是一种相关性计算(后面我们会详细讲解),用以计算不同特征/图像块之间的相关性,结果指标用来反应其匹配程度大小,我们通过这种先行的匹配计算来组合高层特征,可以说为网络后续的匹配关系学习提供了强有力的指导。
总结来说,FlowNet-C 首先从两个图像中提取特征,然后类似于标准匹配方法,人为模仿标准的匹配过程,比较这些特征向量。
1.2 Expanding part 解码/扩展部分
在解码/扩展阶段(如上图所示),该阶段主要包括多次上采样操作,用以恢复图像尺寸和信息。为了更好地融合来自不同层的语义信息,每一层的输入除了上一层的输出外,还有利用上一层输出预测的“光流”和来自编码器对应层的特征。这样我们既保留了从较粗糙的特征图中传递的高级信息,又保留了较低层特征图中提供的精细局部信息。
每一次上采样增加两倍分辨率,重复 4 次该过程,得到一个预测输出流。注意其分辨率仍然比输入图像原尺寸小 4 倍,后续使用双线性插值恢复即可。因为文章发现,与全图像分辨率计算成本较低的双线性插值上采样相比,从该分辨率继续进行网络学习对结果并不会有大的改善,所以可以直接双线性插值得到和输入相同分辨率的光流预测图。
2.Correlation layer 详解
Correlation Operation 是一种相关性匹配的计算,其计算结果表示两个图象块(image patch)的匹配程度。与FlowNetS相比,FlowNetC并不是简单的将输入图像堆叠到一起,而是需要人为地给予网络如何匹配图像细节的指导信息,对两个图片中的高层提取特征进行合并和激活,于是便引入了 Correlation layer。
Correlation Operation 的具体计算过程本质上是一步CNN中的卷积运算,只不过相比CNN中使用特定的卷积核进行卷积,这里使用一个数据(image1 patch)对另外一个数据(image2 patch)做卷积操作,因此该操作并不包含训练参数。对于 image1(w,h,c) 中以 x1 为中心上下延展长度k(矩形块的长宽为 2k+1)的矩形图像块(patch)来说,其与image2(w,h,c) 中以 x2 为中心上下延展长度k的矩形图像块(patch)之间的一次Correlation计算可以表示为:
其实就是用第一个图象的patch对第二个图象的patch做卷积运算(对应内积),一次Correlation计算产生一个结果数字,表示这两个patch的匹配程度。则对于 image1 中的某个像素点 x1 的patch来说,理论上其应该与 image2 中所有像素点的patch(共 w*h 个patch)进行匹配计算,那么 x1 就对应产生一个长度为 w*h 的匹配向量,则对于整个image1和image2来说,其Correlation结果是四维的。
计算一次Correlation就会产生 ![]() 次乘法, 理论上对于 image1 中的每个像素点的 patch 我们都需要与 image2 中的所有 patch 进行匹配计算,则比较所有的patch就会涉及
次乘法, 理论上对于 image1 中的每个像素点的 patch 我们都需要与 image2 中的所有 patch 进行匹配计算,则比较所有的patch就会涉及 ![]() 次这样的乘法计算。但问题在于,这样的计算量是巨大的,因此我们需要对这个过程进行优化。
次这样的乘法计算。但问题在于,这样的计算量是巨大的,因此我们需要对这个过程进行优化。
文章假设对应像素点的位移只存在于一个固定的范围内。这样在真正计算相关联信息时,模型只需要维持一个固定大小的查找窗,超出这个查找窗范围之外的东西便不予考虑了。给定最大查找范围 d,则对于每个位置 x1,我们可以限制 x2 仅在大小(长宽)为 D = 2d + 1 的矩形查找窗中来计算相关性 c(x1, x2)。同时文章使用步幅 s1 和 s2,全局量化 x1 并在以 x1 为中心的邻域内量化和计算 x2。这样对于 image1 中的某个像素点 x1 的patch来说,优化后其应该与 image2 中位于对应查找窗范围内的像素点的patch(共 D*D 个patch)进行匹配计算,那么 x1 就对应产生一个长度为 D*D 的匹配向量,则对于整个image1和image2来说,其Correlation结果可以表示为 ![]() 。在原论文中,设置 parameters k = 0, d = 20, s1 = 1,s2 = 2,在代码中其是通过 c++ 实现的,部分关键源代码如下:
。在原论文中,设置 parameters k = 0, d = 20, s1 = 1,s2 = 2,在代码中其是通过 c++ 实现的,部分关键源代码如下:
template
//一次 Correlation Operation 计算过程
__global__ void correlation_forward(scalar_t* __restrict__ output, const int nOutputChannels,
const int outputHeight, const int outputWidth, const scalar_t* __restrict__ rInput1,
const int nInputChannels, const int inputHeight, const int inputWidth,
const scalar_t* __restrict__ rInput2, const int pad_size, const int kernel_size,
const int max_displacement, const int stride1, const int stride2) {
int32_t pInputWidth = inputWidth + 2 * pad_size;
int32_t pInputHeight = inputHeight + 2 * pad_size;
int32_t kernel_rad = (kernel_size - 1) / 2;
int32_t displacement_rad = max_displacement / stride2;
int32_t displacement_size = 2 * displacement_rad + 1;
int32_t n = blockIdx.x;
int32_t y1 = blockIdx.y * stride1 + max_displacement;
int32_t x1 = blockIdx.z * stride1 + max_displacement;
int32_t c = threadIdx.x;
int32_t pdimyxc = pInputHeight * pInputWidth * nInputChannels;
int32_t pdimxc = pInputWidth * nInputChannels;
int32_t pdimc = nInputChannels;
int32_t tdimcyx = nOutputChannels * outputHeight * outputWidth;
int32_t tdimyx = outputHeight * outputWidth;
int32_t tdimx = outputWidth;
int32_t nelems = kernel_size * kernel_size * pdimc;
// element-wise product along channel axis
for (int tj = -displacement_rad; tj <= displacement_rad; ++tj) {
for (int ti = -displacement_rad; ti <= displacement_rad; ++ti) {
//get center x2,y2 in image2
int x2 = x1 + ti * stride2;
int y2 = y1 + tj * stride2;
float acc0 = 0.0f;
for (int j = -kernel_rad; j <= kernel_rad; ++j) {
for (int i = -kernel_rad; i <= kernel_rad; ++i) {
// THREADS_PER_BLOCK
#pragma unroll
for (int ch = c; ch < pdimc; ch += blockDim.x) {
int indx1 = n * pdimyxc + (y1 + j) * pdimxc
+ (x1 + i) * pdimc + ch;
int indx2 = n * pdimyxc + (y2 + j) * pdimxc
+ (x2 + i) * pdimc + ch;
acc0 += static_cast(rInput1[indx1] * rInput2[indx2]);
}
}
}
if (blockDim.x == warpSize) {
__syncwarp();
acc0 = warpReduceSum(acc0);
} else {
__syncthreads();
acc0 = blockReduceSum(acc0);
}
if (threadIdx.x == 0) {
int tc = (tj + displacement_rad) * displacement_size
+ (ti + displacement_rad);
const int tindx = n * tdimcyx + tc * tdimyx + blockIdx.y * tdimx
+ blockIdx.z;
output[tindx] = static_cast(acc0 / nelems);
}
}
}
} 原始的 c++ 实现用起来比较复杂,因此目前也出现了很多第三方 Correlation 计算的 Python 包,我们直接引入就可以使用了,比如 spatial_correlation_sampler/spatial_correlation_sample 等。
(1)spatial_correlation_sampler/spatial_correlation_sample
input (B x C x H x W) -> output (B x PatchH x PatchW x oH x oW)
- patch 大小
patch_size表示整个矩形patch的长宽,而不仅仅是半径。stride1现在是stride,stride2现在是dilation_patch,其行为类似于扩张卷积- 等价的
max_displacement就是dilation_patch * (patch_size - 1) / 2。- 要为flownetc获得正确的参数,需要设置
kernel_size=1 patch_size=21, stride=1, padding=0, dilation_patch=2
def correlate(input1, input2):
out_corr = spatial_correlation_sample(input1,
input2,
kernel_size=1,
patch_size=21,
stride=1,
padding=0,
dilation_patch=2)
# collate dimensions 1 and 2 in order to be treated as a
# regular 4D tensor
b, ph, pw, h, w = out_corr.size()
out_corr = out_corr.view(b, ph * pw, h, w)/input1.size(1)
return F.leaky_relu_(out_corr, 0.1)3.更多实现细节
FlowNet-S 和 FlowNet-C 在网络结构上大体一致:在收缩部分它们有 9 个卷积层,其中 6 个步长 stride 为 2,每个卷积后都有一个 ReLU 非线性激活函数。卷积核的大小在第一卷积层为 7×7,后面两层为 5×5,从第四层开始都为 3×3。特征图 channel 的数量在每层之后大约加倍,步幅为 2。
网络使用 endpoint error (EPE) 作为训练损失,这是光流估计的标准误差度量。其含义为预测的光流矢量和对应 ground truth 之间的欧几里德距离,并对所有像素取平均。
文章选择 Adam 作为梯度下降的优化方法,其中 Adam 的参数固定为:β1 = 0.9 和 β2 = 0.999。除此之外,网络输入图像的 mini-batche 数量设置为8个图像对。对于学习率来说, FlowNet-C 的网络结构以 λ = 1e−6 的低学习率开始进行训练,在 10k 次迭代后慢慢增加以达到 λ = 1e−4 , 然后在前 300k 之后每 100k 次迭代将其除以 2。
文章还发现,在测试期间放大输入图像可能会提高性能,于是对于 FlowNetS,文章不进行放大,但对于 FlowNetC,文章选择了放大 1.25 倍。由于所使用的数据集在对象类型和包含的运动信息等方面存在很大的不同,一个标准的解决方案是不断微调目标数据集上的网络和参数。
4.关键代码实现(以FlowNet-C为例)
(1)网络结构定义
# 下采样卷积层结构定义
def conv(batchNorm, in_planes, out_planes, kernel_size=3, stride=1):
if batchNorm:
return nn.Sequential(
nn.Conv2d(in_planes, out_planes, kernel_size=kernel_size, stride=stride, padding=(kernel_size-1)//2, bias=False),
nn.BatchNorm2d(out_planes),
nn.LeakyReLU(0.1,inplace=True)
)
else:
return nn.Sequential(
nn.Conv2d(in_planes, out_planes, kernel_size=kernel_size, stride=stride, padding=(kernel_size-1)//2, bias=True),
nn.LeakyReLU(0.1,inplace=True)
)
# 上采样反卷积层结构定义
def deconv(in_planes, out_planes):
return nn.Sequential(
nn.ConvTranspose2d(in_planes, out_planes, kernel_size=4, stride=2, padding=1, bias=False),
nn.LeakyReLU(0.1,inplace=True)
)
# 光流估计的输出层
def predict_flow(in_planes):
return nn.Conv2d(in_planes,2,kernel_size=3,stride=1,padding=1,bias=False)
# corrlation 相关性计算: 引用第三方 spatial_correlation_sample 包
def correlate(input1, input2):
out_corr = spatial_correlation_sample(input1,
input2,
kernel_size=1,
patch_size=21,
stride=1,
padding=0,
dilation_patch=2)
# collate dimensions 1 and 2 in order to be treated as a
# regular 4D tensor
b, ph, pw, h, w = out_corr.size()
out_corr = out_corr.view(b, ph * pw, h, w)/input1.size(1)
return F.leaky_relu_(out_corr, 0.1)
class FlowNetC(nn.Module):
expansion = 1
def __init__(self,batchNorm=True):
super(FlowNetC,self).__init__()
self.batchNorm = batchNorm
# image 的特征提取流(两输入图象处理流一致)
self.conv1 = conv(self.batchNorm, 3, 64, kernel_size=7, stride=2)
self.conv2 = conv(self.batchNorm, 64, 128, kernel_size=5, stride=2)
self.conv3 = conv(self.batchNorm, 128, 256, kernel_size=5, stride=2)
self.conv_redir = conv(self.batchNorm, 256, 32, kernel_size=1, stride=1)
# 收缩部分的后处理下采样流
self.conv3_1 = conv(self.batchNorm, 473, 256)
self.conv4 = conv(self.batchNorm, 256, 512, stride=2)
self.conv4_1 = conv(self.batchNorm, 512, 512)
self.conv5 = conv(self.batchNorm, 512, 512, stride=2)
self.conv5_1 = conv(self.batchNorm, 512, 512)
self.conv6 = conv(self.batchNorm, 512, 1024, stride=2)
self.conv6_1 = conv(self.batchNorm,1024, 1024)
# 扩张部分的上采样流
self.deconv5 = deconv(1024,512)
self.deconv4 = deconv(1026,256)
self.deconv3 = deconv(770,128)
self.deconv2 = deconv(386,64)
# 扩张部分的光流估计层
self.predict_flow6 = predict_flow(1024)
self.predict_flow5 = predict_flow(1026)
self.predict_flow4 = predict_flow(770)
self.predict_flow3 = predict_flow(386)
self.predict_flow2 = predict_flow(194)
# 光流上采样操作
self.upsampled_flow6_to_5 = nn.ConvTranspose2d(2, 2, 4, 2, 1, bias=False)
self.upsampled_flow5_to_4 = nn.ConvTranspose2d(2, 2, 4, 2, 1, bias=False)
self.upsampled_flow4_to_3 = nn.ConvTranspose2d(2, 2, 4, 2, 1, bias=False)
self.upsampled_flow3_to_2 = nn.ConvTranspose2d(2, 2, 4, 2, 1, bias=False)
for m in self.modules():
if isinstance(m, nn.Conv2d) or isinstance(m, nn.ConvTranspose2d):
kaiming_normal_(m.weight, 0.1)
if m.bias is not None:
constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
constant_(m.weight, 1)
constant_(m.bias, 0)
def forward(self, x):
x1 = x[:,:3]
x2 = x[:,3:]
# 1.提取 image1 的高层特征 (batch,h,w,3) -> (batch,h/8,w/8,256)
out_conv1a = self.conv1(x1)
out_conv2a = self.conv2(out_conv1a)
out_conv3a = self.conv3(out_conv2a)
# 2.提取 image2 的高层特征 (batch,h,w,3) -> (batch,h/8,w/8,256)
out_conv1b = self.conv1(x2)
out_conv2b = self.conv2(out_conv1b)
out_conv3b = self.conv3(out_conv2b)
# 3.进一步提取 image1 与 corr 匹配后的特征融合 (batch,h/8,w/8,256) -> (batch,h/8,w/8,32)
out_conv_redir = self.conv_redir(out_conv3a)
# 4. corr 相关性匹配计算 (batch,h/8,w/8,D*D)
out_correlation = correlate(out_conv3a,out_conv3b)
# 5. 在 channel 方向将进一步提取的特征与corr融合作为后续输入 (batch,h/8,w/8,c)
in_conv3_1 = torch.cat([out_conv_redir, out_correlation], dim=1)
# 6. 下采样操作 (batch,h/8,w/8,c) -> (batch,h/64,w/64,1024)
out_conv3 = self.conv3_1(in_conv3_1)
out_conv4 = self.conv4_1(self.conv4(out_conv3))
out_conv5 = self.conv5_1(self.conv5(out_conv4))
out_conv6 = self.conv6_1(self.conv6(out_conv5))
# 7.refinement 上采样/扩张部分
# (1)upconv1: 输出本层预测光流flow6+本层的上采样输出
# - flow6 (batch,h/64,w/64,2)
# - out_deconv5 (batch,h/32,w/32,,512)
flow6 = self.predict_flow6(out_conv6)
flow6_up = self.upsampled_flow6_to_5(flow6)
out_deconv5 = self.deconv5(out_conv6)
concat5 = torch.cat((out_conv5, out_deconv5, flow6_up), 1) # 拼接下层输入 = 本层输出deconv + 收缩部分上下文输出 + 本层输出预测光流
# (2)upconv2: 输出本层预测光流flow5+本层的上采样输出
# - flow5 (batch,h/32,w/32,2)
# - out_deconv4 (batch,h/16,w/16,256)
flow5 = self.predict_flow5(concat5)
flow5_up = self.upsampled_flow5_to_4(flow5)
out_deconv4 = self.deconv4(concat5)
concat4 = torch.cat((out_conv4, out_deconv4, flow5_up), 1)
# (3)upconv3: 输出本层预测光流flow4+本层的上采样输出
# - flow4 (batch,h/16,w/16,2)
# - out_deconv3 (batch,h/8,w/8,256)
flow4 = self.predict_flow4(concat4)
flow4_up = self.upsampled_flow4_to_3(flow4)
out_deconv3 = self.deconv3(concat4)
concat3 = torch.cat((out_conv3, out_deconv3, flow4_up), 1)
# (4)upconv4: 输出本层预测光流flow3+本层的上采样输出
# - flow3 (batch,h/8,w/8,2)
# - out_deconv2 (batch,h/4,w/4,256)
flow3 = self.predict_flow3(concat3)
flow3_up = self.upsampled_flow3_to_2(flow3)
out_deconv2 = self.deconv2(concat3)
concat2 = torch.cat((out_conv2a, out_deconv2, flow3_up), 1)
# 输出最终预测光流 flow2 (batch,h/4,w/4,2)
flow2 = self.predict_flow2(concat2)
if self.training:
return flow2,flow3,flow4,flow5,flow6
else:
return flow2
def weight_parameters(self):
return [param for name, param in self.named_parameters() if 'weight' in name]
def bias_parameters(self):
return [param for name, param in self.named_parameters() if 'bias' in name](2)网络训练
# EPE Loss
def EPE(input_flow, target_flow):
return torch.norm(target_flow-input_flow,p=2,dim=1).mean()
def realEPE(output, target):
b, _, h, w = target.size()
upsampled_output = F.interpolate(output, (h,w), mode='bilinear', align_corners=False)
return EPE(upsampled_output, target)
# 多尺度训练损失(flow2~flow6的EPE损失求和权重不同)
def multiscaleEPE(network_output, target_flow, weights=None):
def one_scale(output, target):
b, _, h, w = output.size()
# 为防止 target 和 output 尺寸不一,使用插值方式来统一图像尺寸
target_scaled = F.interpolate(target, (h, w), mode='area')
return EPE(output, target_scaled)
loss = 0
for output, weight in zip(network_output, weights):
loss += weight * one_scale(output, target_flow)
return loss
# 网络训练主体框架
def run(train_loader,val_loader,model):
best_EPE = -1
# 定义 Adam 优化器
param_groups = [{'params': model.bias_parameters(), 'weight_decay': args.bias_decay},
{'params': model.weight_parameters(), 'weight_decay': args.weight_decay}]
optimizer = torch.optim.Adam(params=param_groups,lr=0.0001,betas=(0.9, 0.999))
# 定义学习率调整策略 lr_scheduler.MultiStepLR
# milestones : epochs at which learning rate is divided by 2
scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[100,150,200], gamma=0.5)
for epoch in range(args.start_epoch, args.epochs):
# 调整学习率 lr
scheduler.step()
# train for one epoch
train_loss, train_EPE = train(train_loader, model, optimizer, epoch)
print(train_loss,train_EPE)
# evaluate on validation set
with torch.no_grad():
EPE = validate(val_loader, model, epoch)
if best_EPE < 0:
best_EPE = EPE
best_EPE = min(EPE, best_EPE)
# 单轮训练
def train(train_loader, model, optimizer, epoch):
global n_iter, args
# training weight for each scale, from highest resolution (flow2) to lowest (flow6)
multiscale_weights = [0.005, 0.01, 0.02, 0.08, 0.32]
# value by which flow will be divided. Original value is 20 but 1 with batchNorm gives good results
div_flow = 20
losses = 0.0
flow2_EPEs = 0.0
epoch_size = len(train_loader) if args.epoch_size == 0 else min(len(train_loader), args.epoch_size)
# switch to train mode
model.train()
for i, (input, target) in enumerate(train_loader):
target = target.to(device)
input = input.to(device)
# compute output
output = model(input)
# compute loss
loss = multiscaleEPE(output, target, weights=multiscale_weights) # 多尺度训练损失
flow2_EPE = 20 * realEPE(output[0], target) # 最终输出光流flow2的单独损失
# record loss and EPE
losses += loss.item()
flow2_EPEs += flow2_EPE.item()
# compute gradient and do optimization step
optimizer.zero_grad()
loss.backward()
optimizer.step()
n_iter += 1
if i >= epoch_size:
break
return losses, flow2_EPEs二.FlowNet 2.0及其后续
FlowNet 2.0 相比于FlowNet来说,其特点就是堆叠多个FlowNetC/FlowNetS子网络来构建更大型的网络结构,逐步细化输出流并得到了更好的效果,其网络结构如下。后来随着光流深度学习的进一步发展,更涌现了大量的新网络和新优化思想,比如PWC-Net等,我们将在后续的文章中进一步讲解和分析。