数据结构 | 各种排序算法梳理 | 复习版

本篇基于Fire_Cloud_1大佬的超棒博客和菜鸟教程的排序算法教程，并结合以往笔记，对所涉及到的排序算法进行梳理，主要用于期末复习，重点侧重于算法思想。

学习目标

• 能清楚给定一个序列在不同排序算法下不同趟后的结果（明确思路）
• 知道相关特征（复杂度、稳定性）

---

冒泡排序

笔记博客链接：实验2 排序算法

动图演示

基本思想

每次冒泡依次比较相邻元素，并将相邻元素的较大(小)元向右移动，每一次会把最大(小)的换至最右，并重复这一操作。

数据的顺序排好之后，冒泡算法仍然会继续进行下一轮的比较，直到size-1次，后面的比较没有意义的。如何优化❓

• 设置标志位judge
• 如果发生了交换，judge设置为true；如果没有交换就设置为false。
• 这样当一轮比较结束后如果judge仍为false即这一轮没有发生交换，说明数据的顺序已经排好，没有必要继续进行下去，实现及时终止。

代码实现

template<class T>
void bubbleSort(T *array,int n)
{
    int temp;//交换用临时变量
    bool judge = true;//标志是否继续交换
	for (int i = 0;judge && (i < n-1);i++)
	{
        //每次遍历标志位都要先置为false，才能判断后面的元素是否发生了交换
		bool judge = false;
	    for(int j = n-1;j > i;j--)
	    {//把array[0:n-1]中最大元素移到右边 
	    	if(array[j] < array[j-1])
			{
				temp = array[j];
                array[j] = array[j-1];
                array[j-1] = temp;
                //只要有发生交换，judge就置为true
			    judge = true;
	     	}
		}	
	}
 } 

时间复杂度：O($n^2$)

---

选择排序

笔记博客链接：实验2 排序算法

动图演示

基本思想

遍历全部数组，把最小的往前排（把最大的往后排也可以）

• 在长度为N的无序数组中，第一次遍历n-1个数，找到最小的数值与第一个元素交换

• 第二次遍历n-2个数，找到最小的数值与第二个元素交换；

  …

• 第n-1次遍历，找到最小的数值与第n-1个元素交换，排序完成。

数据的顺序排好之后，选择排序算法仍然会继续进行下一轮的选择，直到n-1次，后面的比较同样也是没有意义的，优化方法同冒泡排序，实现及时终止。

• 设置标志位judge
• 如果发生了最小值(最大值)更新，judge设置为true；如果没有就设置为false。
• 这样当一轮比较结束后如果judge仍为false即说明数据的顺序已经排好，没有必要继续进行下去，实现及时终止。

代码实现

template<class T>
void selectionSort(T *array,int n)
{
    int temp;
	bool judge = true;
	for(int i = 0;judge && (i < n-1);i++)//终止条件 
	{
		int Min = i;
		judge = false;
		for(int j = i+1;j < n;j++)
		{
			if(array[Min] > array[j]) Min = j;
			else judge = true;
		}
        if(Min != i)
        {
           int temp = array[i];
           array[i] = array[Min];
           array[Min] = temp;
       }
	}
}

时间复杂度：O($n^2$)

---

插入排序

笔记博客链接：实验2 排序算法

动图演示

基本思想

把每一个元素依次作为插入元素 ，找到合适的位置插入，维护一个有序列。（就和玩扑克牌理扑克牌顺序一个道理）

• 采用升序插入排序，即先把数组的第一个元素视为已排序元素
• 后将第二个元素拿去插入，若比第一个小，就插到第一个前，反之插到其后
• 再把第三个元素拿去插入，和前两个元素都比较，找到合适的位置。
• 以此类推。

代码实现

template<class T>
void insertSort(T *array,int n) 
{
	for (int i = 1;i < n;i++)
	{
		T x = array[i];//把每一个元素依次作为插入元素 
		int j;
		for(j = i-1;j >= 0 && x < array[j];j--)
		{
			array[j + 1] = array[j];
		}
		array[j + 1] = x;
	}
}

时间复杂度：O($n^2$)

---

桶排序

笔记博客链接：第六章：线性表链式描述

动图演示

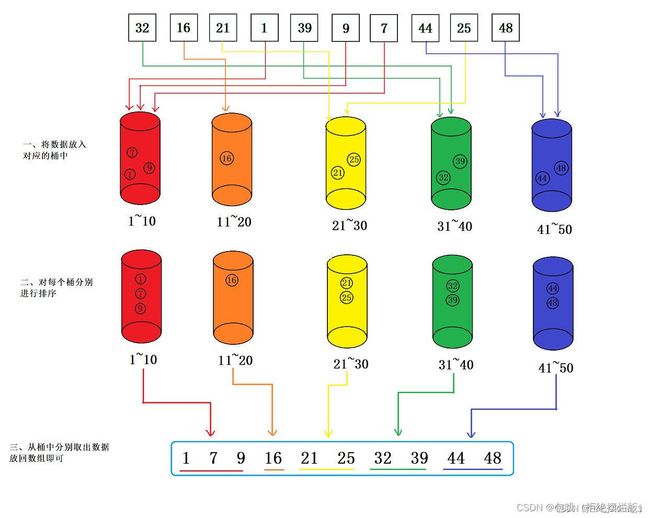
基本思想

• 分配：将待排序的数组(链表)中每一个数根据他们的范围一一放入对应的桶中

• 排序：在每一个桶的内部分别对其进行排序(这里的排序考虑那些内部排序)

• 收集：从第一个桶开始，将其中的数据一一放回原数组(链表)

  第六章笔记有一个链表桶排序例子

因为桶的个数和大小都是我们人为设置的。而每个桶又要避免空桶的情况。所以我们在使用桶排序的时候即需要对待排序数列要求偏均匀，又要要求桶的设计兼顾效率和空间。

有一个范围设定参考公式：范围gap = (max - min + 1)/桶数

在元素分配时：元素值整除(gap + 1)落到对应的桶

代码实现

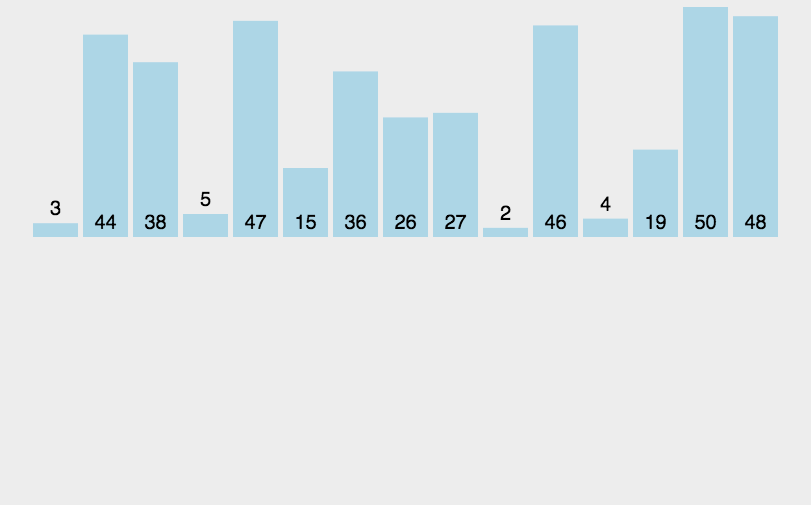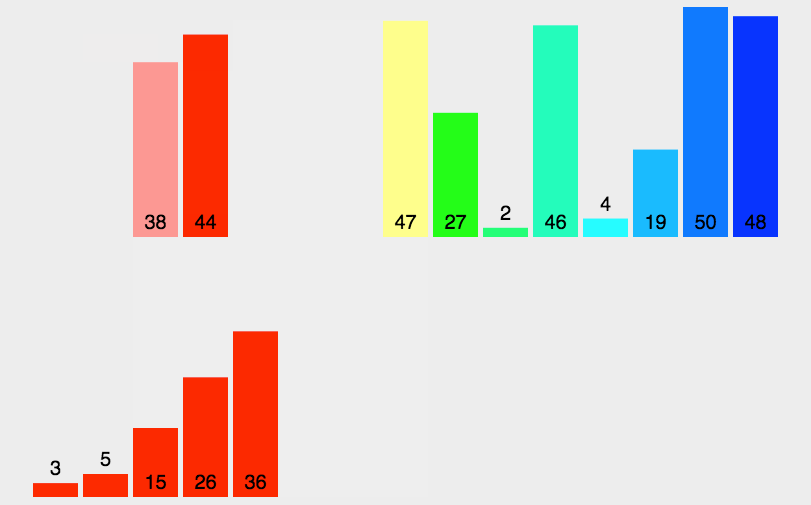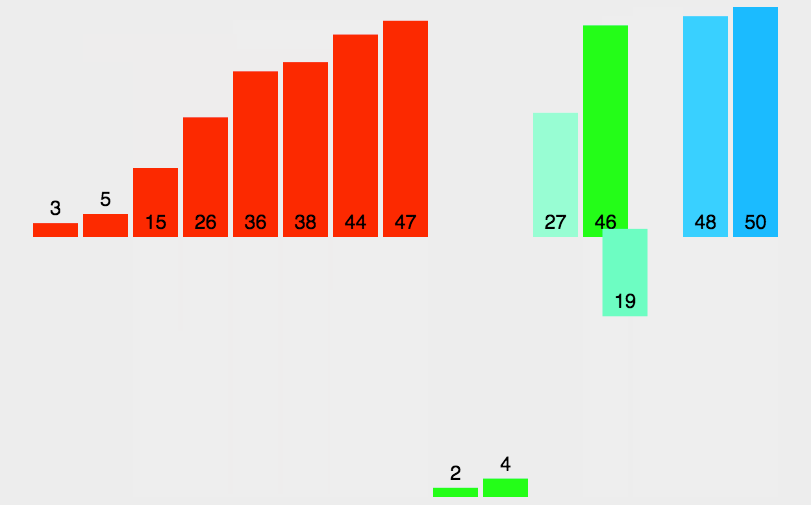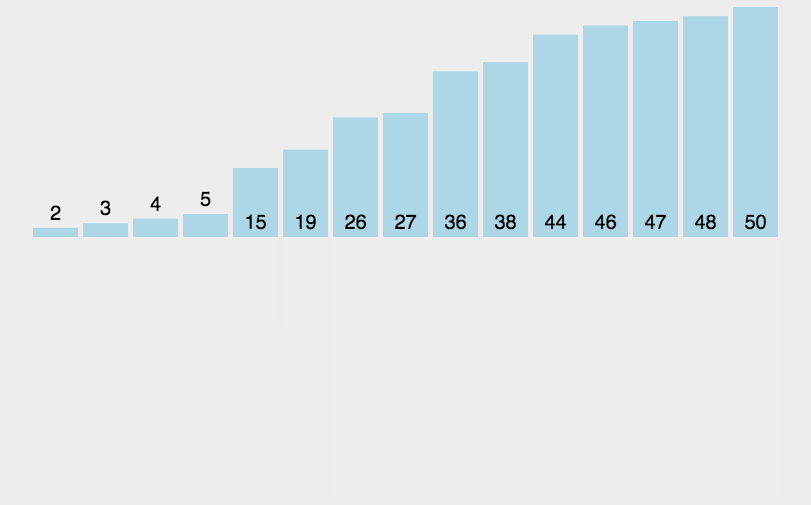
针对这一组数据，gap = 9，以下为该组数据的数组实现

void BucketSort(int* a, int n)
{
	int bucket[5][5];// 分配五个桶。
	int bucketsize[5];// 每个桶中元素个数的计数器。

	// 初始化桶和桶计数器。
	memset(bucket, 0, sizeof(bucket));
	memset(bucketsize, 0, sizeof(bucketsize));

	// 把数组a的数据按照范围放入对应桶中
	for (int i = 0; i < n; ++i)
	{
		bucket[a[i] / 10][bucketsize[a[i] / 10]++] = a[i];
	}

	// 分别对每个桶中的数据进行排序
	for (int i = 0; i < 5; ++i)
	{//这里用的是快速排序
		QuickSort(bucket[i], 0, bucketsize[i] - 1);
	}

	// 将把每个桶中的数据依次放回数组a中
	int index = 0;
	for (int i = 0; i < 5; ++i)
	{
		for (int j = 0; j < bucketsize[i]; ++j)
		{
			a[index++] = bucket[i][j];
		}
	}
}

时间复杂度：O($n+k$)，n是数据规模，k是桶数

---

基数排序

笔记博客链接：第六章：线性表链式描述

动图演示

基本思想

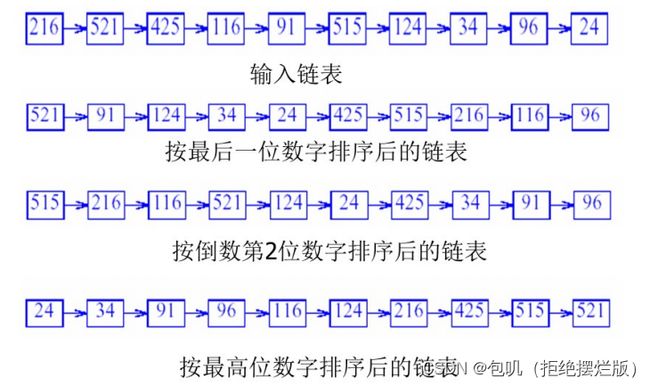
将整数按某种基数r切割成不同的数字，然后对数字依次进行排序。一般是按基数10，因此直接按位数分解。

应用举例

(重点关注方法，给出链表序列能给出第n趟之后的序列)

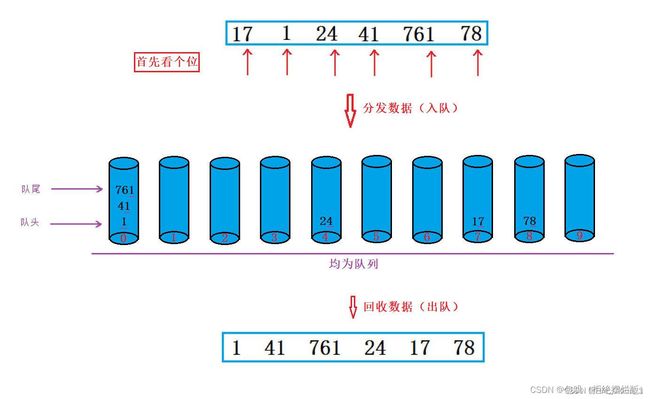
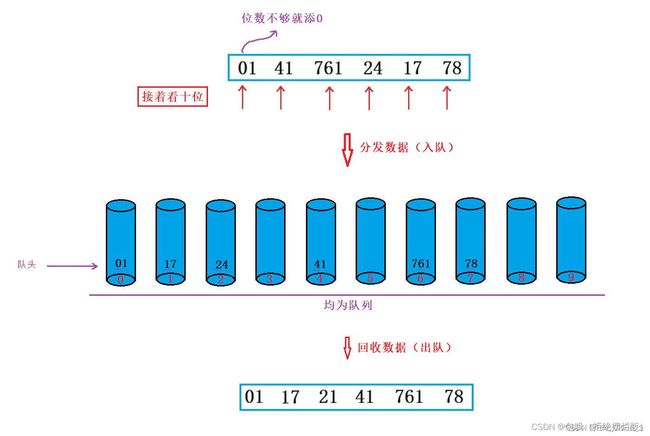
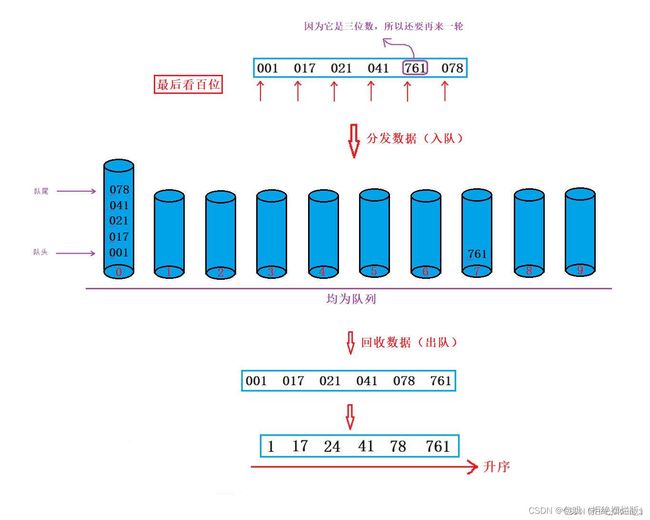
扩展：用队列实现

基本思路：

• 每一数位排序要完成分发和回收，且要实现先分发入桶中的数据先回收出来，基于队列后，【分发数据】就是【尾插】，【回收数据】就是【头删】
• 针对要比较几次：在分发数据前我们应该先去求出这些数中最大的那个数，然后再求出这个数的位数，那它的位数多少位，那就需要比较多少次

算法图解:

代码实现

#include 
#define RADIX 10		//表示基数的个数
queue<int> qu[RADIX];	//定义桶（每个桶均为一个队列）

//主体代码
void RadixSort(int* a, int n)		
{
	//首先求出数组中的最大值
	int max = GetMax(a, n);
	//求出最大值的位数
	int k = GetDigit(max);
	
	//进行k次的数据分发和回收
	for (int i = 0; i < k; ++i)
	{
		//分发数据
		Distribute(a, n, i);
		//回收数据
		Collect(a);
	}
}

//-------------功能补充------------------
//求解数组中的最大值
int GetMax(int* a, int n)
{
	int max = a[0];
	for (int i = 0; i < n; ++i)
	{
		if (a[i] > max)
			max = a[i];
	}
	return max;
}

//求解最大值的位数
int GetDigit(int num)
{
	//num : 10000
	int count = 0;
	while (num > 0)
	{
		count++;
		num /= 10;
	}
	return count;
}

//获取数位逻辑
int GetKey(int value, int k)
{
	int key = 0;
	while(k >= 0)
	{
		key = value % 10;
		value /= 10;
		k--;
	}
	return key;
}

//分发数据逻辑
void Distribute(int* a, int n, int k)
{
	for (int i = 0; i < n; ++i)
	{
		int key = GetKey(a[i], k);
		qu[key].push(a[i]);
	}
}

//回收数据逻辑
void Collect(int* a)
{
	int index = 0;
	for (int i = 0; i < RADIX; ++i)
	{
		while (!qu[i].empty())
		{
			a[index++] = qu[i].front();
			qu[i].pop();
		}
	}
}

时间复杂度：O($n\times k$)，n是数据规模，k是桶数

---

堆排序

笔记博客链接：

• 第十二章：优先级队列，在了解堆排序之前，一定要先学习堆的相关概念
• 实验10.1 堆的操作

动图演示

算法思想

• 将要排序的n个元素初始化为一个大（小）根堆

• 每次从堆中提取（即删除）元素。

• 即初始化+依次pop

• 初建小根堆操作后，输出一次top，就pop一下，pop完后又是合规的小根堆就又把top输出，这个过程就是如上的依次pop操作从而实现排序，并借助依次输出top(即根)实现了升序输出。
  • 如果想让降序输出，可以尝试将每次pop掉的存入栈，存完再出去，依据后进先出，实现小根堆堆排序降序输出。

图解示例

代码实现

这里贴的就是实验10.1的代码

#include
using namespace std;

//将一个一维数组的长度从oldLength变成newLength。（后续push操作会用到） 
template<class T>
void changeLengthID(T*& array, int oldLength, int newLength)
{
    T* newarray = new T[newLength];//函数首先分配一个新的、长度为newLength的数组   
    int number = (oldLength < newLength) ? oldLength : newLength; //取min {oldLength, newLength} 
    for (int i = 0; i < number; i++)
		newarray[i] = array[i];//然后把原数组的前min {oldLength, newLength} 个元素复制到新数组中
    delete[] array;//释放原数组所占用的空间                      
    array = newarray;//将新数组赋值到旧数组完成更改 
}

//小根堆定义及实现 
template<class T>
class minHeap
{
	public:
    	minHeap(int initialCapacity = 10)
		{//构造 
    		arrayLength = initialCapacity + 1;
    		heap = new T[arrayLength];
    		heapSize = 0;
		}
    	~minHeap() { delete[] heap; }//析构 
    	const T& top()
    	{//返回优先级最大的元素的引用 
    		return heap[1];
    	}
    	void pop();//删除
		void push(const T&theElement);//插入
    	void initialize(T*theHeap, int theSize);//初始化 
    	void output(ostream& out) const;//输出 
	private:
		T* heap;//一个类型为T的一维数组 
		int arrayLength;//数组heap的容量 
    	int heapSize;//堆的元素个数               
};

//小根堆的插入 
template<class T>
void minHeap<T>::push(const T& theElement)
{//把元素theElement加入堆
    
	//必要时增加数组长度 
	if (heapSize == arrayLength - 1)
    {//数组长度加倍 
        changeLengthID(heap, arrayLength, 2 * arrayLength);
        arrayLength *= 2;
    }
    
	//为元素theElement寻找插入位置 
	//小根堆要求老叶子比新叶子小 
    int currentNode = ++heapSize;//currentNode从新叶子向上移动，就从最底下开始 
    while (currentNode != 1 && heap[currentNode / 2] > theElement)
    {//这个时候老叶子比新叶子大，不能把元素放在这 
        heap[currentNode] = heap[currentNode / 2]; //把大的那个元素赋给currentNode，相当于把大的元素往下移 
        currentNode /= 2;//同时把currentNode（一个打算插入theElement的位置）移向双亲，就往上移                    
    }
    //循环结束，即找到合适的位置插入 
    heap[currentNode] = theElement;
}

//删除操作是针对堆顶元素而言的，即把末尾元素移动到堆顶，再自顶向下(重复构建堆的操作)，递归调整。
template<class T>
void minHeap<T>::pop()
{
	//删除堆顶元素
    heap[1].~T(); 
	//删除最后一个元素，然后重新建堆（这一步相当于把末尾元素拿出来） 
    T lastElement = heap[heapSize--];
	//开始给拿出来的末尾元素找合适的放入位置，从顶开始，自顶向下调整 
    int currentNode = 1,
        child = 2;//currentNode的孩子    
    while (child <= heapSize)
    {
    	//heap[child]应该是currentNode的更大的孩子（就是说它的值太大了，应该往后头放） 
        if (child < heapSize && heap[child] > heap[child + 1])
            child++;
		
		//可以把lastElement放在heap[currentNode]吗？ 
		//可以 
        if (lastElement <= heap[child])
            break; 
		//不可以（以下操作和上述push相关操作同理） 
        heap[currentNode] = heap[child];//把孩子child向上移动 
        currentNode = child;//向下移动一层寻找位置          
        child *= 2;
    }
    heap[currentNode] = lastElement;
}

//初始化一个非空小根堆 
template<class T>
void minHeap<T>::initialize(T* theHeap, int theSize)
{//在数组theHeap[1:theSize]中建小根堆（参考p304-305) 
    delete[] heap;
    heap = theHeap;
    heapSize = theSize;
	
	//堆化 
    for (int root = heapSize / 2; root >= 1; root--)
    {
        T rootElement = heap[root];

        int child = 2 * root; 
        while (child <= heapSize)
        {	
        	//heap[child]应该是兄弟中的较小者 
            if (child < heapSize && heap[child] > heap[child + 1])
                child++;
                
			//可以把rootElement放在heap[child / 2]吗? 
			//可以（原理同上 
            if (rootElement <= heap[child])
                break;  
            //不可以 
            heap[child / 2] = heap[child]; 
            child *= 2;                   
        }
        heap[child / 2] = rootElement;
    }
}

int main(void)
{
    int m, n;
    cin >> n;
    minHeap<int> minheap(n);
    for (int i = 0; i < n; i++) 
	{
        int num;
        cin >> num;
        minheap.push(num);
    }
    cout << minheap.top() << endl;
    cin >> m;
    for (int i = 0; i < m; i++) 
	{
        int op, num;
        cin >> op;
        if (op == 1)
		{
            cin >> num;
            minheap.push(num);
            cout << minheap.top() << endl;
        }
        if (op == 2) 
		{
            minheap.pop();
            cout << minheap.top() << endl;
        }
        if (op == 3) 
		{
            int p;
            cin >> p;
            minHeap<int> minheap1(p);
            for (int i = 0; i < p; i++) 
			{
                int number;
                cin >> number;
                minheap1.push(number);
            }
            for (int i = 0; i < p; i++) 
			{
                cout << minheap1.top() << " ";
                minheap1.pop();
            }
        }
    }
    return 0;
}

时间复杂度：O($nlogn$)

---

归并排序

笔记博客链接：第十八章：分而冶之

动图演示

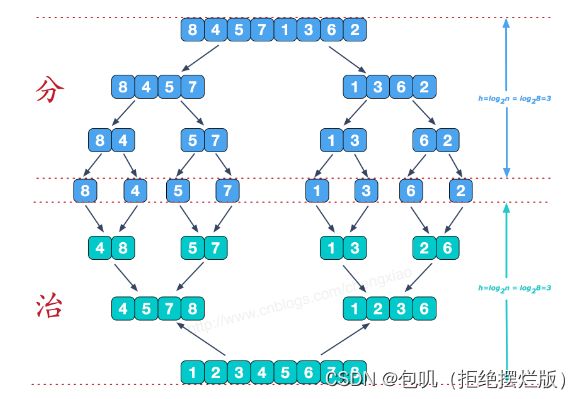
算法思想

• 利用分而治之方法进行排序算法：
• 将n个元素按非递增顺序排列
  • 若n为1，算法终止；
  • 否则
    • 将这一元素集合分割成两个或更多个子集合
    • 对每一个子集合分别排序
    • 将排好序的子集合归并为一个集合
• 即 先使每个子序列有序，再使子序列段间有序

代码实现

template<class T>
void mergeSort(T a[],int n)
{//使用归并排序算法对a[0:n-1]进行排序
	T*b = new T[n];
	int segmentSize = 1;//段的大小
    while(segmentSize < n)
    {
		mergePass(a,b,segmentSize,n);//从a归并到b 
        segmentSize += segmentSize;
		mergePass(b,a,segmentSize,n);//从b归并到a 
        segmentSize += segmentSize;
    }
}

template<class T>
void mergePass(T x[],T y[],int segmentSize,int n)
{
	int i = 0;
	while(i <= n-2*segmentSize)
    {//归并两个大小为segmentSize的相邻段
        merge(x,y,i,i+segmentSize-1,i+2*segmentSize-1);
        i = i+2*segmentSize;
    }
	//剩下不足2*segmentSize个元素
    if(i+segmentSize < n)
		merge(x,y,i,i+segmentSize-1,n-1);
	else 
        for(int j = i;j <= n-1;j++)
			y[j] = x[j];//把最后一段复制到y
}

template<class T>
void merge(T c[],T d[],int startOfFirst,int endOfFirst,
int endOfSecond)
{
	int first = startOfFirst,//第一段的游标
		second = endOfFirst+1,//第二段的游标
    	result = startOfFirst;//结果段的游标
	//当两个被归并段都未处理完，则不断进行归并
    while((first <= endOfFirst) && (second <= endOfSecond))
    {
        if(c[first] <= c[second]) 
            d[result++] = c[first++];
		else 
            d[result++] = c[second++];
    }
	//考虑余下的部分
	if (first > endOfFirst)
    {
        //剩下第二段
		for(int q = second;q <= endOfSecond;q++)
			d[result++] = c[q];
    }
	else 
    {
        for(int q = first;q <= endOfFirst;q++)
            d[result++] = c[q];
    }
}

时间复杂度：O($nlogn$)

---

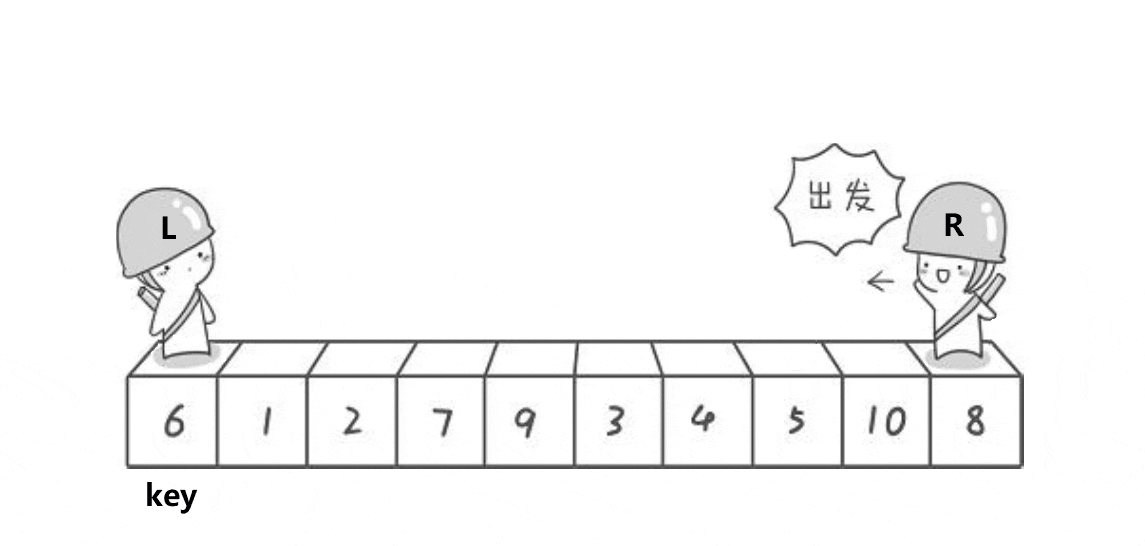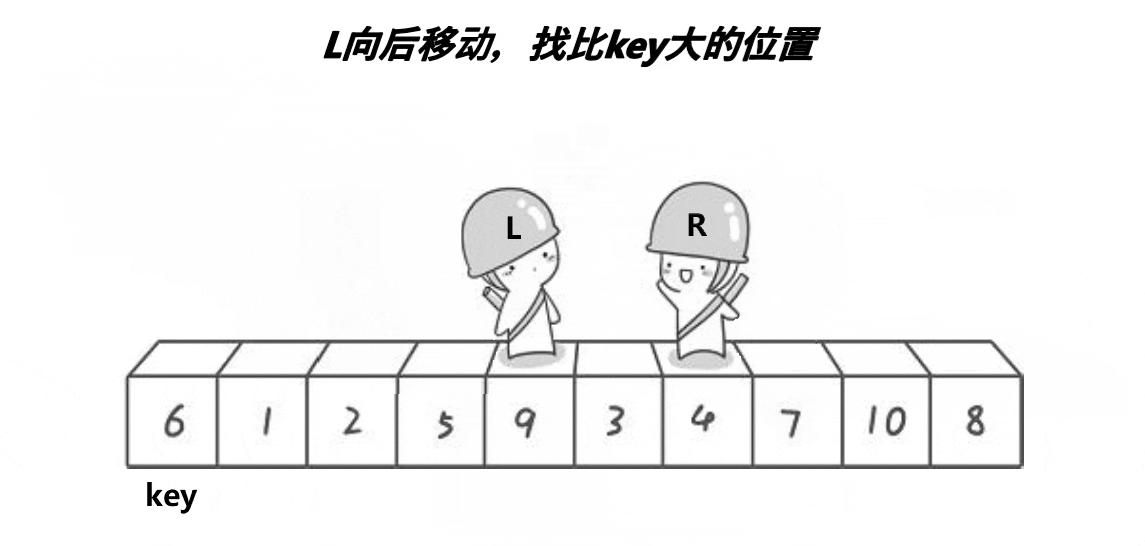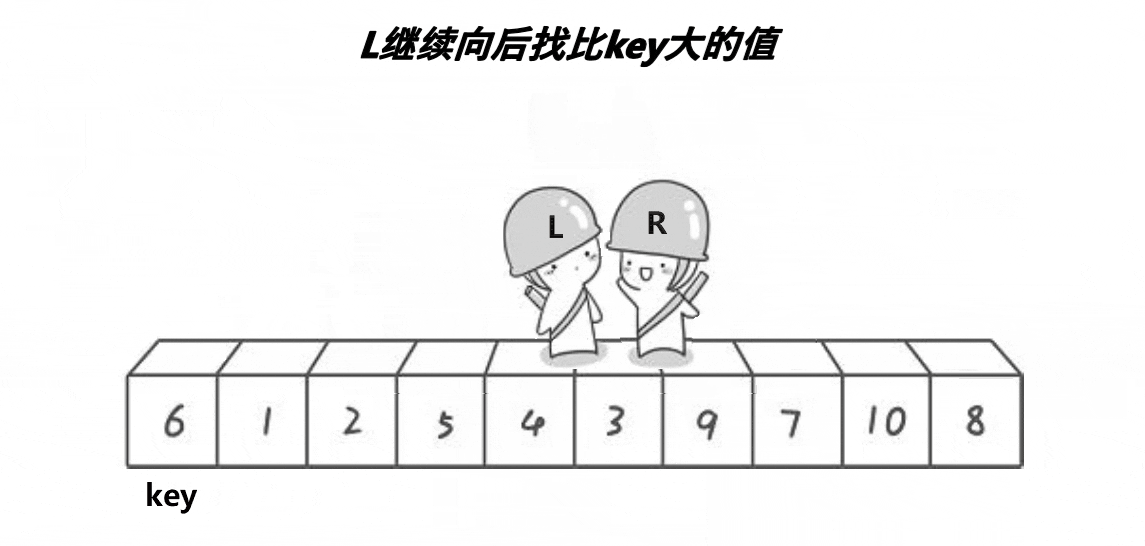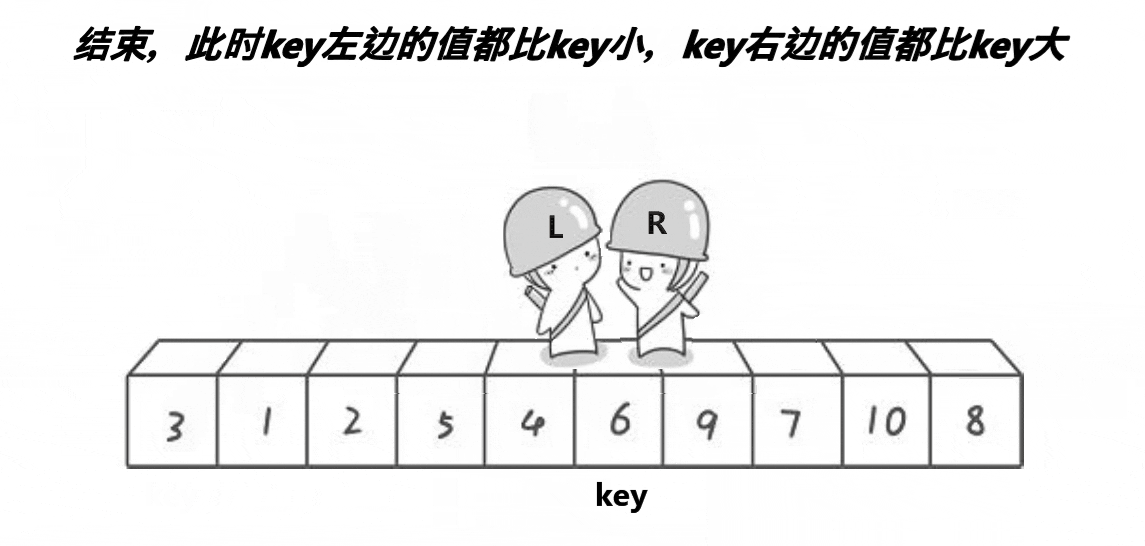
快速排序

笔记博客链接：第十八章：分而冶之

动图演示

算法思想

• 从数列中取出一个数作为基准数
• 分区
  • 将比这个数大的数全放到它的右边
  • 小于或等于它的数全放到它的左边
• 再对左右区间重复第二步，直到各区间只有一个数

代码实现

void Sort(node *array,int low,int high)//排序
{
	if(low > high) return;//排好了，不运行了
	int i,j;
	node index;
	node index;
	index = array[low];//定义基准数 
	i = low;
	j = high;
 	while(i < j)
	{
  		while(i < j && array[j].weight >= index.weight)
  		{
  			//从右往左找比基准数小的
   			j--;
		}	
		if(j > i) 
		{
			//交换array[i]和array[j]，并把i右移一位 
			array[i++] = array[j];
		}
		while(i < j && array[i].weight < index.weight)
		{
			//从左往右找比基准数大的
			i++;
		}
		if(j > i) 
		{	
			//交换array[i]和array[j]，并把j左移一位
			array[j--] = array[i];
		}
	}
 	array[i] = index;//基准点归位
 	Sort(array,low,i-1);//递归调用快排比基准点小的元素
 	Sort(array,i+1,high);//递归调用快排比基准点大的元素
}

时间复杂度：O($nlogn$)

---

名次排序补充

也出现过，所以也放它进来吧，但是它似乎没有趟的概念

笔记博客链接：实验2 排序算法

一句话思路

先计算每个元素的具体位置，再将其移动到相应位置

代码实现

template<class T>
void rankSort(T *array,int n) 
{
	T *new_array = new T [n];//创建附加数组 
	int assist[100]; 
	for(int i = 0;i < n;i++)
    {
       assist[i] = 0;
    }
    for(int i = 1;i < n;i++)
    {
        for(int j = 0;j < i;j++)
        {
            if(array[j] <= array[i])
                assist[i]++;
            else 
                assist[j]++;      
        }
    }
	for (int i = 0;i < n;i++)
	{
        //利用辅助数组，按照名次将array[i]暂时贴到新开辟的new_array[]中 
		new_array[assist[i]] = array[i];
	}
	for (int j = 0;j < n;j++)
	{
		array[j] = new_array[j];//将数组array重新进行赋值操作
	}	
	delete []new_array;
}

---

比较总结

• n：数据规模
• k："桶"的个数
• In-place：占用常数内存，不占用额外内存
• Out-place：占用额外内存
• 稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同