【深度学习】深度学习小结01

---

1. 基本概念

1.1 机器学习与深度学习

人工智能、机器学习、神经网络、深度学习四者关系

---

1.2 概述

人工智能

人工智能是类人思考、类人行为，理性的思考、理性的行动。人工智能的基础是哲学、数学、经济学、神经科学、心理学、计算机工程、控制论、语言学。人工智能的发展，经过了孕育、诞生、早期的热情、现实的困难等数个阶段；

人工智能是什么？

---

机器学习

根据有无标记（label）机器学习可分为：

• 监督学习：
  • 就是通过已有的训练样本（即已知数据以及其对应的输出）去训练得到一个最优模型（这个模型属于某个函数的集合，最优则表示在某个评价准则下是最佳的），再利用这个模型将所有的输入映射为相应的输出，对输出进行简单的判断从而实现分类的目的，也就具有了对未知数据进行分类的能力。
  • 简单来说就是通过对有标记的数据的学习，建立一个模型函数来预测新数据的标记。
  • 典型的例子就是KNN、SVM。
• 无监督学习：
  • 它与监督学习的不同之处，在于我们事先没有任何训练样本，而需要直接对数据进行建模。
  • 简单来说就是通过对无标记的训练数据的学习，揭示数据的内在性质及规律。
  • 无监督学习里典型的例子就是聚类了。

机器学习入门好文，强烈推荐

---

神经网络

神经网络是一门重要的机器学习技术，是机器学习中的一种模型，是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。

神经网络按照层数多少可分为：

• 单层神经网络（感知机）
• 两层神经网络（多层感知机）
• 多层神经网络（深度学习）

感知机
感知机是最简单的人工神经网络——只有一个神经元的单层神经网络，可以完成简单的线性分类任务。

可以看到，一个感知器有如下组成部分：
通过6个问题进一步理解

(1) 感知机的定义是什么？
感知机(perceptron)是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别。
(2) 感知机的取值是什么？
取+1和-1二值。
(3) 感知机对应于输入空间(特征空间)中的什么？
感知机对应于输入空间中将实例划分为正负两类的分离超平面，属于判别模型。
(4) 感知机学习的目的是什么？
感知机学习旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。
(5) 感知机学习算法有什么特点？
感知机学习算法具有简单，并且易于实现的特点，分为原始形式和对偶形式。
(6) 什么是感知机预测？
感知机预测是用学习得到的感知机模型对新的输入实例进行分类。它是神经网络与支持向量机的基础。

说明：
上述超平面是指在N维线性空间中维度为N-1的子空间。二维空间中的超平面是一条线，三位空间的超平面是一个二维平面，四维空间的超平面是一个三位体。

什么是感知机？

零基础入门深度学习(1) - 感知器

神经网络——最易懂最清晰的一篇文章

四种基本的神经网络

---

深度学习

深度学习是源于人工神经网络的研究，是基于人工神经网络的机器学习方法族的一部分。学习可以是有监督的、半监督的或无监督的，通常以发现数据的分布式特征表示。

一文看懂深度学习（白话解释+8个优缺点+4个典型算法）

---

2. 神经网络

2.1 神经网络训练

通过调整隐层和输出层的参数，使得神经网络的计算结果与真是结果尽量接近

训练过程：

• 正向传播
• 反向传播

【深度学习】正向传播、反向传播与优化函数

---

2.2 神将网络的设计原则

• 调整网络拓扑结构
• 选择合适的激活函数
• 选择合适的损失函数

激活函数和损失函数

---

2.2.1 过拟合与正则化

2.2.2.1 过拟合

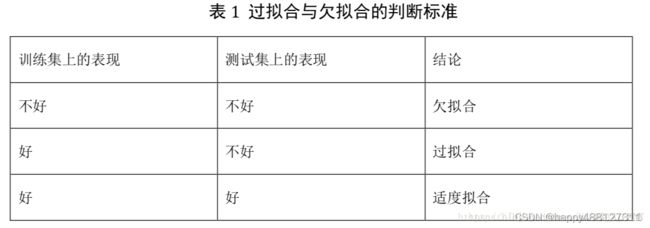
过拟合是指模型过度逼近训练数据，影响力模型的泛化能力。表现为：在训练集上误差很小，在验证数据集上误差很大。一般可以通过正则化来解决。

除了过拟合外，还有欠拟合，即训练特征过少，拟合函数无法有效逼近训练集，造成误差很大。欠拟合一般可以通过增加训练样本或者模型复杂的来解决。

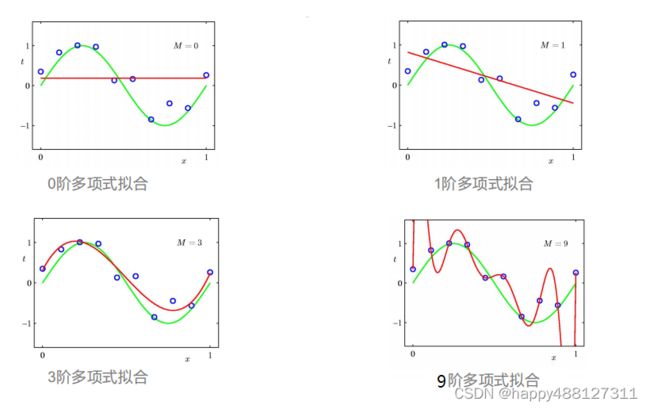
由上图可以看出：

• 0阶多项式和1阶多项式：模型过于简单不能 拟合出sin函数的形状 这种现象叫做欠拟合
• 3阶多项式：刚好拟合出sin函数的图像 这样的拟合效果是理想中的效果
• 9阶多项式：模型过于复杂，虽然把图中所有的数据点都记住了 ，但是模型自身波动很大，对于新的数据不能有好的预测效果，泛化能力差，这种现象叫过拟合。
  

2.2.2.2 正则化

假设上面过拟合图中的曲线方程如下

图4就是一个9次多项式，为了防止过拟合，将其转化为三次多项式，即设法将高次项系数变为0。此时需要给损失函数中增加对高次项的惩罚，即在原损失函数上添加 C₄w₄² + C₅w₅² + … + C₉w₉² ，C为常数。此时用损失函数训练出来的结果w₄ - w₉都约等于0，即可以认为是一个三次多项式。

正则化就是在损失函数中对不想要的部分加入惩罚项，常见的正则化有L1 和 L2

过拟合

过拟合（定义、出现的原因4种、解决方案7种）

【深度学习】正则化（超详解）

---

2.3 简单的神经网络的模型（代码示例）

一个简单的神经网络模型

import time

import torch
import torchvision.datasets
from torch import nn
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
from torch.nn import Sequential, Conv2d, MaxPool2d, Flatten, Linear

# 自定义网络
class MyNN(nn.Module):

    def __init__(self) -> None:
        super().__init__()
        self.model = Sequential(
            Conv2d(3, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 64, 5, padding=2),
            MaxPool2d(2),
            Flatten(),
            Linear(1024, 64),
            Linear(64, 10)
        )

    def forward(self, x):
        x = self.model(x)
        return x

# 搭建网络进行训练
# 1. 准备数据集
train_data = torchvision.datasets.CIFAR10("dataset", train=True, transform=torchvision.transforms.ToTensor(),
                                          download=True)
test_data = torchvision.datasets.CIFAR10("dataset", train=False, transform=torchvision.transforms.ToTensor(),
                                         download=True)
# 查看数据长度
print("训练数据集长度为：{}".format(len(train_data)))
print("测试数据集长度为：{}".format(len(test_data)))

# 2. 加载数据集
train_dataLoader = DataLoader(train_data, batch_size=64)
test_dataLoader = DataLoader(test_data, batch_size=64)

# 3. 创建网络模型
demo_nn = MyNN()

# 4. 损失函数
loss_fn = nn.CrossEntropyLoss()

# 5. 优化器
learning_rate = 0.01

# 随机梯度下降
optimal = torch.optim.SGD(demo_nn.parameters(), lr=learning_rate)

# 记录训练次数
count_train = 0
# 记录测试次数
total_test = 0

# 训练轮数
epoch = 50

# 使用tensorboard
writer = SummaryWriter("loss-train")
start_time = time.time()
for i in range(epoch):
    print("---------开始第{}轮训练---------".format(i + 1))

    # 训练步骤开始
    demo_nn.train() # 将网络设置为训练模式，当网络包含 Dropout, BatchNorm时必须设置，其他时候无所谓
    for data in train_dataLoader:
        imgs, targets = data
        output = demo_nn(imgs)
        # 优化模型
        loss = loss_fn(output, targets)
        # 梯度清零
        optimal.zero_grad()
        # 反向传播
        loss.backward()
        # 训练
        optimal.step()
        # 纪录训练次数
        count_train += 1
        # item()函数会直接输出值，比如tensor(5),会输出5
        if count_train % 100 == 0:
            # 记录时间
            end_time = time.time()
            print(end_time - start_time)
            print("训练次数为{}时，loss值为{}".format(count_train, loss.item()))
            # 记录训练loss值
            writer.add_scalar("train_loss", loss.item(), count_train)

    total_test = 0
    total_accuracy = 0

    # 将网络设置为测试模式，当网络包含 Dropout, BatchNorm时必须设置，其他时候无所谓
    demo_nn.eval()
    with torch.no_grad():
        for data in test_dataLoader:
            imgs, targets = data
            output = demo_nn(imgs)
            loss = loss_fn(output, targets)
            # 记录测试数据集loss和
            total_test += loss.item()
            # 求预测结果精确度之和
            # argmax:求最大值的下标，1按行求，0按列求
            accuracy = (output.argmax(1) == targets).sum()
            total_accuracy += accuracy

    print("测试集的整体loss为{}".format(total_test))
    print("测试集的整体准确度为{}".format(total_accuracy / len(test_data)))
    writer.add_scalar("accuracy", total_accuracy / len(test_data), i)
    # 记录测试loss,
    writer.add_scalar("test_loss", total_test, i)

    # 保存每一步训练的模型
    torch.save(demo_nn, "train-model/train_model_{}.pth".format(i))
    print("第{}次训练模型已保存".format(i + 1))

writer.close()

---

注：本博客内容来教材和自网络整理，仅作为学习笔记记录，不用做其他用途。