激活函数sigmoid、tanh、relu

转载自《动手学深度学习》(PyTorch版)
在线书籍：https://tangshusen.me/Dive-into-DL-PyTorch
github：https://github.com/ShusenTang/Dive-into-DL-PyTorch

激活函数

在不引入激活函数的神经网络中，多层神经网络经过线性变换，仍然等价于一个单层的神经网络。例如：只有一层的全连接神经网络公式为：
$$H=X{W}_o+b_o$$

在增加一层隐藏层后：
$$H=X{W}_o+b_h$$
$$O=H{W}_o+b_o$$
将上面两个公式联立起来，可以得到：
$$O=(X{W}_h+b_h)W_o+b_o=X{W}_h{W}_o+b_h{W}_o+b_o.$$
我们可以发现，虽然仍引入了一层隐藏层，但是还是可以通过线性变换，转换成一个单层的神经网络。添加更多的隐藏层，只是让系数更加复杂而已。

解决上述问题就是引入激活函数，将线性变换转变为非线性变换。

同时，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

1. sigmoid函数

sigmoid函数可以将元素的值变换到0和1之间：

$$sigmoid(x)=\frac{1}{1+e^{-x}}$$

sigmoid函数在早期的神经网络中较为普遍，但它目前逐渐被更简单的ReLU函数取代。在后面“循环神经网络”一章中我们会介绍如何利用它值域在0到1之间这一特性来控制信息在神经网络中的流动。下面绘制了sigmoid函数。当输入接近0时，sigmoid函数接近线性变换。

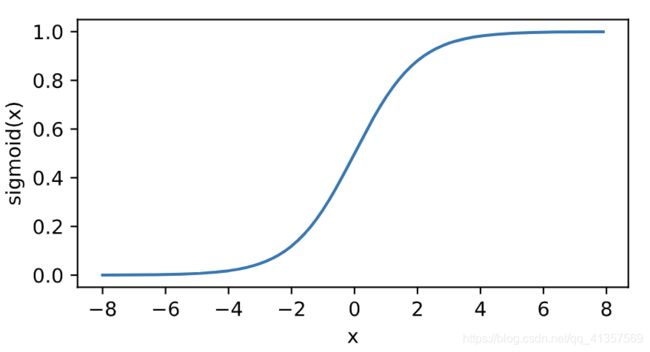
依据链式法则，sigmoid函数的导数

$$sigmoi{d}^{\prime }(x)=sigmoid(x)(1-sigmoid(x))$$

下面绘制了sigmoid函数的导数。当输入为0时，sigmoid函数的导数达到最大值0.25；当输入越偏离0时，sigmoid函数的导数越接近0。

优点：

1. Sigmoid函数的输出在(0,1)之间，输出范围有限，优化稳定，可以用作输出层。
2. 连续函数，便于求导。

缺点：

1. sigmoid函数在变量取绝对值非常大的正值或负值时会出现饱和现象，意味着函数会变得很平，并且对输入的微小改变会变得不敏感。在反向传播时，当梯度接近于0，权重基本不会更新，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。
2. sigmoid函数的输出不是0均值的，会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响。
3. 计算复杂度高，因为sigmoid函数是指数形式。

2. tanh函数

tanh（双曲正切）函数可以将元素的值变换到-1和1之间：

$$tanh(x)=\frac{1-exp(-2x)}{1+exp(-2x)}$$

绘制tanh函数。当输入接近0时，tanh函数接近线性变换。虽然该函数的形状和sigmoid函数的形状很像，但tanh函数在坐标系的原点上对称。

依据链式法则，tanh函数的导数

$$tan{h}^{\prime }(x)=1-tan{h}^2(x)$$

下面绘制了tanh函数的导数。当输入为0时，tanh函数的导数达到最大值1；当输入越偏离0时，tanh函数的导数越接近0。

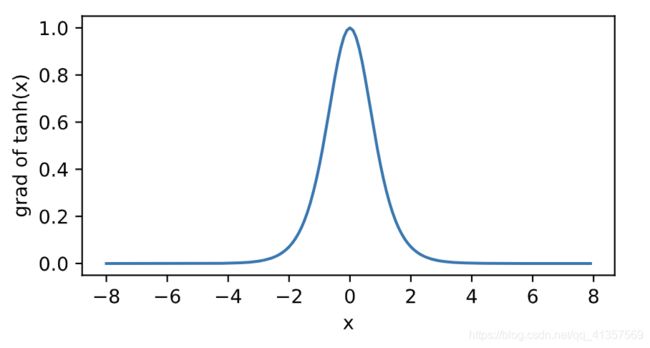
优缺点：

• Tanh函数是 0 均值的，因此实际应用中 Tanh 会比 sigmoid 更好。
• 但是仍然存在梯度饱和与exp计算的问题。

3. relu函数

ReLU（rectified linear unit）函数提供了一个很简单的非线性变换。给定元素xx，该函数定义为

可以看出，ReLU函数只保留正数元素，并将负数元素清零。

$$relu(x)=\{\begin{array}{ll}0& \text{x <= 0}\\ x& \text{x > 0}\end{array}$$

当输入为负数时，ReLU函数的导数为0；当输入为正数时，ReLU函数的导数为1。尽管输入为0时ReLU函数不可导，但是我们可以取此处的导数为0。下面绘制ReLU函数的导数。

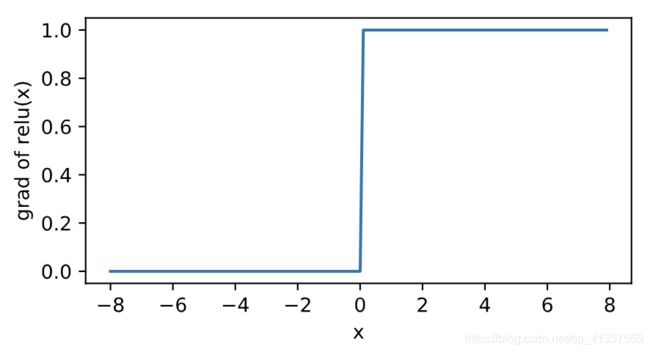
优点：

1. 使用ReLU的SGD算法的收敛速度比 sigmoid 和 tanh 快。
2. 在x>0区域上，不会出现梯度饱和、梯度消失的问题。
3. 计算复杂度低，不需要进行指数运算，只要一个阈值就可以得到激活值。

缺点：

1. ReLU的输出不是0均值的。
2. Dead ReLU Problem(神经元坏死现象)：ReLU在负数区域被kill的现象叫做dead relu。ReLU在训练的时很“脆弱”。在x<0时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新。

产生这种现象的两个原因：参数初始化问题；learning rate太高导致在训练过程中参数更新太大。

解决方法：采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。