【笔记】动手学深度学习 - 卷积层
从全连接到卷积
主要是应用于图片识别,其次还有自然语言处理等。
卷积神经网络不再是对每个输入像素进行处理,而是把图片分成一小块区域来进行处理,这样就加强了图片信息的连续性。加深了神经网络对于图片的理解和识别。
这里卷积部分看的不是特别懂,所以又去看了吴恩达的深度学习视频。
视频中的这个式子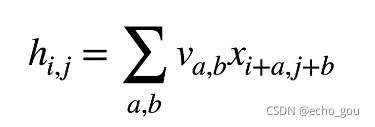 就是对应吴恩达视频中的这个
就是对应吴恩达视频中的这个![]() 没有加偏置的效果。其中a,b就是用来限制过滤器的大小的。
没有加偏置的效果。其中a,b就是用来限制过滤器的大小的。
计算机视觉的网络结构具有两个性质:
平移不变性(translation invariance):不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为“平移不变性”。
局部性(locality):神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系,这就是“局部性”原则。最终,在后续神经网络,整个图像级别上可以集成这些局部特征用于预测。
卷积层
这部分可以参考吴恩达深度学习部分
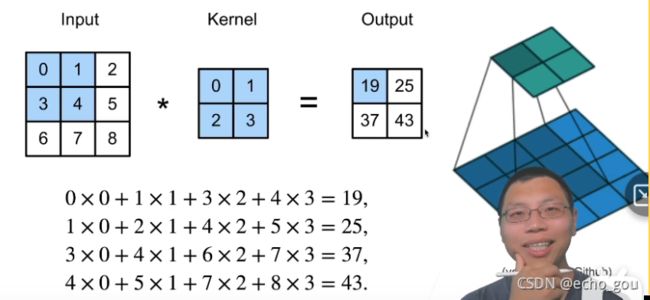
二维相关,通常也可以叫做二维卷积。
输入、核、输出之间的大小关系:
总结:
1 卷积层就是将输入和核矩阵(过滤器)进行交叉相关,加上偏移后得到输出。
2 核矩阵和偏移是可以学习的参数
3 核矩阵的大小是超参数
代码
这里定义了一个矩阵X
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
我们想要通过卷积出矩阵Y(卷积核为[1,-1]的一个1*2矩阵)
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])
我们的目的就是通过真实的X,Y(定义好了的)来训练出[1,-1]这样的卷积核:
import torch
from torch import nn
from d2l import torch as d2l
"""卷积运算。"""
def corr2d(X, K): #X为输入的矩阵,K为过滤器
h, w = K.shape #得到过滤器的大小
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1)) #定义输出的矩阵,大小由输入矩阵和过滤器的大小决定
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i:i + h, j:j + w] * K).sum() #每次从X矩阵中取出一部分和过滤器进行点积然后求和 得到Y[i,j]
return Y
"""定义网络,网络forward即为对X用K来卷积后加上bias得到Y"""
class Conv2D(nn.Module):
def __init__(self, kernel_size):
super().__init__()
self.weight = nn.Parameter(torch.rand(kernel_size))
self.bias = nn.Parameter(torch.zeros(1))
def forward(self, x):
return corr2d(x, self.weight) + self.bias
"""Y=X用K来卷积"""
X = torch.ones((6, 8))
X[:, 2:6] = 0
print('X:',X)
K = torch.tensor([[1.0, -1.0]])
Y = corr2d(X, K)
print('Y',Y)
# 构造一个二维卷积层,它具有1个输出通道和形状为(1,2)的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)
# 这个二维卷积层使用四维输入和输出格式(批量大小、通道、高度、宽度),
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
for i in range(10):
Y_hat = conv2d(X) #输出值为Y_hat
l = (Y_hat - Y) ** 2 #损失函数
conv2d.zero_grad() #梯度设为零
l.sum().backward()
# 迭代卷积核
conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad #梯度下降
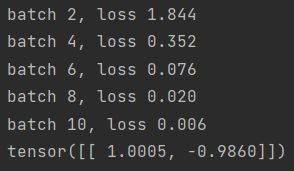
if (i + 1) % 2 == 0:
print(f'batch {i+1}, loss {l.sum():.3f}')
print(conv2d.weight.data.reshape((1, 2)))