数学建模——数据包络分析步骤及程序详解
数学建模——数据包络分析步骤及程序详解
文章目录
- 数学建模——数据包络分析步骤及程序详解
- 前言
- 一、数据包络分析介绍
-
- 1、原理
- 2、CCR模型
- 3、BCC模型
- 4、CCR和BBC的实际应用
- 二、代码程序
- 三、实战
-
- 1、结果解读
- 2、模型优缺点
- 总结
-
- 参考资料
前言
数据包络分析(Data envelopment analysis,DEA)是运筹学和研究经济生产边界的一种方法。该方法一般被用来测量一些决策部门的生产效率。这里数据包络分析针对特定的题目比较单一,可以解释的点(水论文)相对较少。但是在特定的产入产出问题优化上,却有着很强的实际应用性,所以被广泛应用在实际生活中,在硕士、博士论文中也很常见。
一、数据包络分析介绍
1、原理
数据包络分析有多种模型,包括CCR模型,BBC模型、交叉模型等等,其中最为常用的就是CCR模型,BBC模型两个模型,我们下面就来认识这两个模型,先认识两个原理:
1.决策单元:决策单元是指可以将一定的输入转化为相应的产出的运营实体。即由投入到产出的过程。
2.有效前沿:投入固定时,对于产出集合D,我们无论如何改变生产组合都不能使得产出超过D,则称(X,Y)为有效生产活动,此投入产出对应一个前沿,由众多“有效生产”构成的凸包即为前沿。
数据包络分析其本质原理是通过DMU 的输入和输出数据进行综合分析,得出每个DMU效率的相对指标,然后将所有DMU效率指标排序,确定相对有效的 DMU ,同时还可以用投影方法指出非 DEA 有效或者 弱 DEA有效的原因,以及应该改进的方向和程度,为管理人员提供管理决策信息。
2、CCR模型
CCR模型是最早也最经典的DEA模型,通过“投入一定数量的生产要素,并产出一定数量的产品的经济系统来判断各个单元的相对合理性和有效性。从投入资源的角度来看,在当前产出的水准下,比较投入资源的使用情况,以此作为效益评价的依据,这种模式称为“投入导向模式”。
用大白话来说就是投入是固定的,产出要尽可能的多。
模型如下:
假设数据可以分为n个DMU(样本个数),m个输入(投入)变量,s个输出(产出)变量,向量 X i = ( x 1 i , x 2 i , ⋯ , x m i ) X_i=(x_{1i},x_{2i},\cdots,x_{mi}) Xi=(x1i,x2i,⋯,xmi)表示第 i i i个决策单元(样本)的输入变量,向量 Y i = ( y 1 i , y 2 i , ⋯ , y s i ) Y_i=(y_{1i},y_{2i},\cdots,y_{si}) Yi=(y1i,y2i,⋯,ysi)表示第 i i i个决策单元(样本)的输出变量。
定义决策单元j的效率评价指数为:
h i = u T Y j v T X j , i = 1 , 2 , ⋯ , n hi=\frac{u^TY_j}{v^TX_j},i=1,2,\cdots,n hi=vTXjuTYj,i=1,2,⋯,n
其中, u T = ( u 1 , u 2 , ⋯ , u m ) u^T=(u_1,u_2,\cdots,u_m) uT=(u1,u2,⋯,um), v T = ( v 1 , v 2 , ⋯ , v m ) v^T=(v_1,v_2,\cdots,v_m) vT=(v1,v2,⋯,vm), u = u i u=u_i u=ui为第 i i i个投入的权重, v i v_i vi为第 i i i个产出的权重。
评价决策单元j的效率数学模型为:
目标函数:
max u T Y j v T X j \max\frac{u^TY_j}{v^TX_j} maxvTXjuTYj
约束条件
s . t . { u T Y j v T X j ≤ 1 u T Y j = 1 u ≥ 0 , v ≥ 0 , s.t.\left\{ \begin{array}{lr} \frac{u^TY_j}{v^TX_j} \le1 \\ u^TY_j=1 \\ u\ge 0,v\ge 0, \\ \end{array} \right. s.t.⎩⎪⎨⎪⎧vTXjuTYj≤1uTYj=1u≥0,v≥0,
是的,CCR模型就是很朴素的一个数学规划模型,目标函数是产出乘权重比上产入乘权重,效率评价指数越大,说明投入产出的效率越高,约束条件就是将投入约定为1,效率评价指数小于1(效率评价指数是无法超过1的,因为你的产出不可能超过你的投入),权重大于0(这里权重和不一定为1,这是决策单元根据最优结果计算出来的,其实应该叫系数更为合适)。
3、BCC模型
BCC模型也是很经典的DEA模型,BCC 模型考虑到在可变规模收益 (VRS) 情况,即当有的决策单元不是以最佳的规模运行时,技术效益 (Technology efficiency,TE) 的测度会受到规模效率 (Scale efficiency,SE) 的影响。这种模式称为“产出导向模式”。
用大白话来说就是投入是可以持续增加的,研究这种情况下的投入和产出的关系。
因此,在构建 BCC 模型时,我们需要假设规模报酬可变,对 CCR 模型的约束条件进行简单的改进,增加凸性假设条件: ∑ λ j = 1 , j = 1 , 2 , ⋯ , n \sum{\lambda_j}=1,j=1,2,\cdots,n ∑λj=1,j=1,2,⋯,n,即可得数学模型如下:
目标函数:
min θ \min \theta minθ
约束条件:
s . t . { ∑ j = 1 n λ j y j + s + = θ x 0 ∑ j = 1 n λ j y j − s − = θ y 0 ∑ λ j = 1 , j = 1 , 2 , , n s.t.\left\{ \begin{array}{l} \sum\limits_{j=1}^n{\lambda _jy_j+s^+=\theta x_0}\\ \sum\limits_{j=1}^n{\lambda_jy_j-s^-=\theta y_0}\\ \sum{\lambda _j=1,j=1,2,,n}\\ \end{array} \right. s.t.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧j=1∑nλjyj+s+=θx0j=1∑nλjyj−s−=θy0∑λj=1,j=1,2,,n
针对的是规模效率所带来的情况,投入增加的同时,产出是否可以跟得上,最为理想的情况是θ为1的时候,产出跟得上投入。
4、CCR和BBC的实际应用
一般情况单独拎出来CCR模型即可完成数学建模论文的某一个小问,BCC是CCR的进阶模型,通常不再怎么使用,大家只要掌握CCR即可。
我们可以对数据同时做 CCR 模型和 BCC 模型的 DEA 分析来评判决策单元的规模效率 (SE)。如果决策单元 CCR 和 BCC 的技术效益存在差异,则表明此决策单元规模无效,并且规模无效效率可以由 BCC 模型的技术效益和 CCR 模型的技术效益之间的差异计算出来。
CCR 和 BCC 模型只能横向比较决策单元在同一时间点的生产效率,使用时应该注意:有n个样本就要比较n次。
二、代码程序
matlab代码如下:
clear
clc
format long
data=[39414 2823 34877 44562 2036 603 322 934936 929914 1492 29811
54934 1911 52242 35262 3862 908 396 1075563 1030664 1780 29811
96442 2743 88737 303221 4307 1596 694 1104835 1010146 1936 32678
107079 3036 98513 478883 3956 2530 1089 909220 862077 2160 36063
124359 3326 116897 378318 4102 2669 1179 1117851 1123109 2349 38951
140167 3900 130355 261203 4180 3538 1991 1116429 1100510 2446 40324
161523 3989 153722 444755 4309 3727 1593 878466 880226 2637 43211
177681 4669 167161 422267 4630 6629 1867 1048053 1003952 2904 47116
124969 4416 111415 286399 3829 5665 2591 1142395 1112661 3092 49406
146015 3200 129997 228695 5308 4911 2506 1202365 1112475 3252 51119
]';
X=data([1:5],:);%X为输入变量
Y=data([6:11],:);%Y为输出变量
[m,n]=size(X);% m为输入变量个数,n为样本数
s=size(Y,1);%s为一共有多少个输出变量
A=[-X' Y'];
%由于目标函数求最小,这里的-X就转化成了求最大
b=zeros(n,1);
LB=zeros(m+s,1);UB=[];
for i=1:n
f=[zeros(1,m) -Y(:,i)'];
Aeq=[X(:,i)',zeros(1,s)];
beq=1;
w(:,i)=linprog(f,A,b,Aeq,beq,LB,UB);
E(i,i)=Y(:,i)'*w(m+1:m+s,i);
%迭代是为了防止出现linprog出现局部最优的情况
%这种情况比较少见,也可以直接去掉
for j=1:100
w(:,i)=linprog(f,A,b,Aeq,beq,LB,UB,randn(11,1));
D(i,i)=Y(:,i)'*w(m+1:m+s,i);%产出值*产出系数
if D(i,i)Stata代码如下
ssc install dea, replace
dea ivars = ovars [if] [in] [using/filename ][, ///
rts(string) ort(string) stage(#) ///
trace saving(filename) ]
ivars 表示投入变量
ovars 表示产出变量
rts(string) 可选择不同规模报酬的相应模型:默认值是 rts(crs) ,即规模报酬不变 (对应 CCR 模型) , rts(vrs) 、 rts(drs) 和 rts(nirs) 分别表示规模报酬可变 (对应 BCC 模型) ,规模报酬递减和规模报酬不增长
ort(string) 指定方向:默认值是 ort(i) ,表示面向投入的 DEA 模型; ort(o) 表示面向产出的 DEA 模型;面向投入的 DEA 模型是指在至少满足已有的产出水平的情况下最小化投入,而面向产出的 DEA 模型则是指在不需要更多的投入的情况下最大化产出
stage(#) 默认值是 stage(2) ,即两阶段 DEA 模型;stage(1) 为单阶段 DEA 模型
trace 允许所有序列显示在结果窗口中,并保存在 " dea.log " 文件中
注意:需要导入决策单元变量 dmu 。
以下是用matlab数据包络法本质是寻优,所以我自己写了一个模拟退火算法求解,算是作者感兴趣自己写的(有缺陷的,新解的产生没有写好,后续修改完):
clear
clc
format long
data=[39414 2823 34877 44562 2036 603 322 934936 929914 1492 29811
54934 1911 52242 35262 3862 908 396 1075563 1030664 1780 29811
96442 2743 88737 303221 4307 1596 694 1104835 1010146 1936 32678
107079 3036 98513 478883 3956 2530 1089 909220 862077 2160 36063
124359 3326 116897 378318 4102 2669 1179 1117851 1123109 2349 38951
140167 3900 130355 261203 4180 3538 1991 1116429 1100510 2446 40324
161523 3989 153722 444755 4309 3727 1593 878466 880226 2637 43211
177681 4669 167161 422267 4630 6629 1867 1048053 1003952 2904 47116
124969 4416 111415 286399 3829 5665 2591 1142395 1112661 3092 49406
146015 3200 129997 228695 5308 4911 2506 1202365 1112475 3252 51119
]';
X=data([1:5],:);%X为输入变量
Y=data([6:11],:);%Y为输出变量
[m,n]=size(X);% m为输入变量个数,n为样本数
s=size(Y,1);%s为一共有多少个输出变量
A=[-X' Y'];%由于目标函数求最小,这里的-X就转化成了求最大
b=zeros(n,1);
LB=zeros(m+s,1);UB=[];
A=[-X' Y'];
for i=1:n
% f=[zeros(1,m) -Y(:,i)'];
% Aeq=[X(:,i)',zeros(1,s)];
% beq=1;
% w(:,i)=linprog(f,A,b,Aeq,beq,LB,UB);%前3列为投入系数,后2列为产出系数
% E(i,i)=Y(:,i)'*w(m+1:m+s,i);%产出值*产出系数
temperature=1000;%初始温度
iter=1000;%迭代次数
L=1;%用于记录迭代的次数
sj=randi([1,5]);
w=zeros(11,10);
w(sj,i)= 1/X(sj,i);
x=w(:,i);
kns=find(w([1,5],i) ~= 0);
if size(kns)==[0 1]
x=x;
else
kns2=randi([1,length(kns)]);
% aeq=[X(:,i)',zeros(1,s)];
% beq=1;
r = randi([1,5]);
x(r,1)=x(kns(kns2),1)*X(kns(kns2),i)/X(r,i);
end
f=[zeros(1,m) -Y(:,i)']*x;
sj2=randi([6,11]);
x(sj2,1)=1/data(sj2,i);
% [-X' Y']*x <= zeros(n,1);
if x <= 0 %惩罚函数
f=f+1000000*temperature;
elseif A*x > zeros(n,1)
f=f+1000000*temperature;
end
while temperature>0.01
for j=L:iter
%产生新解
kns=find(x([1,5]) ~= 0);
if size(kns)==[0 1]
x1=x;
else
kns2=randi([1,length(kns)]);
r = randi([1,5]);
x1=x;
x1(r,1)=x(kns(kns2),1)*X(kns(kns2),i)/X(r,1);
end
kns3=find(x1([6,11],1) ~= 0);
x1(kns3+5)=x1(kns3+5).*rand(length(kns3),1);
sj2=randi([6,11]);
x1(sj2,1)=1/data(sj2,i)*rand();
f1=[zeros(1,m) -Y(:,i)']*x1;%计算适应度
if x1 <= 0 %惩罚函数
f=f+1000000*temperature;
elseif A*x1 > zeros(n,1)
f=f+1000000*temperature;
end
delta_e=f1-f;
if delta_e<0
x=x1;
else
if exp(delta_e/temperature)>rand()
x=x1;
end
end
end
L=L+1;
%退火的效率
temperature=temperature*0.99;
end
w(:,i)=x;
E(i,i)=Y(:,i)'*w(m+1:m+s,i);%产出值*产出系数
end
theta=diag(E)';
fprintf('用DEA方法对此的相对评价结果为:\n');
disp(theta);
三、实战
1、结果解读
我们就以matlab的结果作为演示分析,希望对大家有所提示
使用matlab输出结果如下:

根据输出的结果,我们可以得到 10 个决策单元的生产效率:2010、2011、2017、2018、2019功5年为 DMU 有效,得分皆为 1;其他年份为 DMU 低效率,得分分别为 0.88、0.85、0.93、0.94、0.86 。
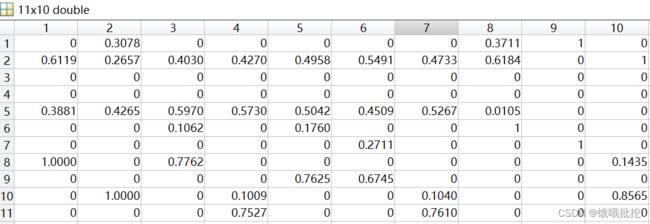
对于2012年(第三列),减少 0.403单位 的 政府拨款 投入、0.597单位 的 R&D人员全时当量 投入与 0.107 单位的 专利申请量 产出、0.107 单位的 新产品产值 产出将使得生产更有效率。对于其他年份做出一样的评价即可。
分析为什么会出现这种情况,后续给茂名市提建议的时候可以针对性的提出。
2、模型优缺点
数据包络分析本身无需输入任何权重,是基于数据本身所求最有权重,从有利于决策单元(样本)的评价,可以避免指标在优先意义确定权重的情况。但是,这也是他的缺点,有些指标的先行行就是天然的高,例如在产出中,结合茂名市的中国特色社会主义道路来说,经济发展是绝对的优先,在论文成果方面可以适当降低。
DEA结构简单,容易理解,使用方便,也易于解释。
总结
现如今 DEA 作为评估组织绩效的管理工具已经得到了相当大的关注,它被广泛用于评估银行、航空公司、医院、大学和制造业等公共部门和私营部门的效率中。而 dea 命令使得决策单元的效率可以在 Stata 中直接进行评估,不再需要同时使用统计分析软件与数据包络分析软件,大大简便了操作。我们可以看到当下很多评估组织效率的论文都使用了 Stata 求解 DEA 模型,我自己喜欢用matlab,所以我用matlab写。然而,这两条命令只能指定上文提及的这些相对基础的模型,要指定 FG 模型、ST 模型、CCGSS 加法模型和具有无穷多个 DMU 的 CCW 模型,还需要对命令作进一步的优化和改进。
以上是我对于数据包络分析的一些拙见,也希望大家可以指点出我的错误。
参考资料
知乎(连玉君):https://zhuanlan.zhihu.com/p/130289495
CSDN(饲养猿):https://blog.csdn.net/qq_48774513/article/details/120198871
百度百科:https://baike.baidu.com/item/%E6%95%B0%E6%8D%AE%E5%8C%85%E7%BB%9C%E5%88%86%E6%9E%90/82754