补充-堆箱子+python(DFS)

题目描述：

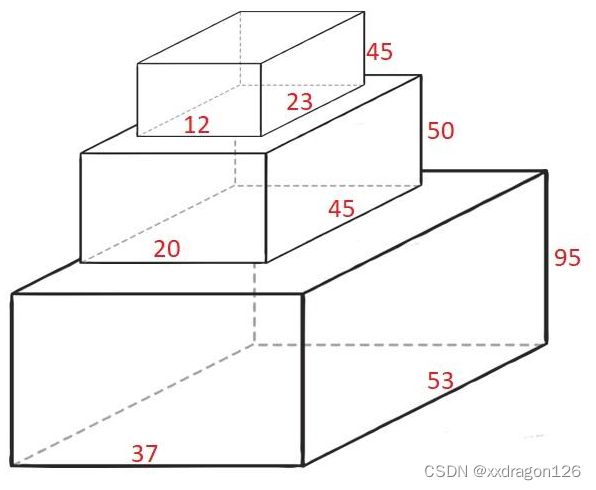
给定n个箱子的长宽高信息（顺序不定，即箱子可以翻转），将它们竖直堆放，求所能堆叠的最大高度。

要求：上方箱子的底面不能超出下方箱子的底面。

其他：以所能获得的最大高度为目标，不必使用所有的箱子。

一 解题思路

# 0 仍将数据转化为矩阵；题目设计寻找所有可行的方案，考虑使用DFS编程求解。

# 1 对长方体的3个属性信息排列组合为3组，每组中前两个属性元素作为底面边长、第3个属性元素作为高。

## 示例：对于长方体的3个属性信息“85 35 23”进行排列组合，得到的3组数据为：[85 35 23]、[85 23 35]、[35 23 85]；使得三个属性值均有机会作为高。

## 1.1 用矩阵存放箱子信息：每行代表一条箱子信息，每条箱子信息包含3个组合数据。

# 2 在堆叠长方体时，每个长方体都有可能放置在最底层；因此，对于N个待堆叠的长方体，这里需要N个循环

##2.1 在将某长方体堆叠在最底层时，它的每条边都有可能作为高，即有三种摆放方式；因此，这里需要3个循环

# 3 判断条件：用于（剪枝）提前终止不可行方案

# 3.1 新堆叠的长方体的底面长和宽（即组合数据中前两个元素中的最大值和最小值，它们分别对应于底面的长和宽），必须分别小于下层长方体的底面的长和宽

# 4 终止条件

# 当访问过所有的箱子之后，终止

# 5 最后返回所能获得的最大高度

# 6 特别地：以获得最大高度为目标，无需将所有箱子都堆叠起来，即不满足3.1条件的箱子可以弃用。

# 6.1 使用DFS全搜，可以自动包含本情况。

二 代码实现

# 补充escape:

# 1 对长方体的3个属性信息排列组合为3组，每组中前两个属性元素作为底面边长、第3个属性元素作为高。
## 示例：对于长方体的3个属性信息“85 35 23”进行排列组合，得到的3组数据为：[85 35 23]、[85 23 35]、[35 23 85]；使得三个属性值均有机会作为高。
## 1.1 用矩阵存放箱子信息：每行代表一条箱子信息，每条箱子信息包含3个组合数据。
# 2 在堆叠长方体时，每个长方体都有可能放置在最底层；因此，对于N个待堆叠的长方体，这里需要N个循环
##2.1 在将某长方体堆叠在最底层时，它的每条边都有可能作为高，即有三种摆放方式；因此，这里需要3个循环
# 3 判断条件：用于（剪枝）提前终止不可行方案
# 3.1 新堆叠的长方体的底面长和宽（即组合数据中前两个元素中的最大值和最小值，它们分别对应于底面的长和宽），必须分别小于下层长方体的底面的长和宽
# 4 终止条件
# 当访问过所有的箱子之后，终止
# 5 最后返回所能获得的最大高度
# 6 特别地：以获得最大高度为目标，无需将所有箱子都堆叠起来，即不满足3.1条件的箱子可以弃用。
# 6.1 使用DFS全搜，可以自动包含本情况。

import collections
import math
#### 数据处理
def proData(size,subdata):
    new_data = []
    ### 将每条原始数据排列组合为3条数据
    for i in range(size):
        temp0 = subdata[i][0]
        temp1 = subdata[i][1]
        temp2 = subdata[i][2]
        temp = [[temp0,temp1,temp2],[temp0,temp2,temp1],[temp1,temp2,temp0]] # 3条组合数据
        new_data.append(temp) # 每一行代表一条长方体数据
    return new_data

### DFS 处理
class Solution:
    def DFS(self):
        self.Max_height = [] # 存放各方案所能获得的最大高度
        ####
        ######### 分别放置各个箱子作为最底层，共size
        for i in range(size):
            #### 获得详细信息信息
            node = new_data[i]
            ### 分别以各组合信息，作为起始
            for j in range(3):
                start = node[j]
                ## 设置初始信息
                sum = 0 # 累积高度
                self.ways = 0 # 初始化本方案所能获得的箱子高度
                queue = [] # 存放已访问过的箱子；即行号i（每个行号代表一种箱子）
                queue.append(i) # 添加已访问的箱子，即行号i
                step = 1 # 计数，即记录已访问过的箱子的个数
                pre_start = [math.inf,math.inf,math.inf] # 由于要比较相邻两个箱子的底边长和宽，因此需要设置变量保存下方箱子的信息
                self.dfs(pre_start,start,sum,step,queue)
                #### 存放当前的箱子高度
                self.Max_height.append(self.ways)
            #### 初始化
        return max(self.Max_height) ## 返回所有方案中的最大高度

    def dfs(self,pre_start,start,sum,step,queue):
        ### 1 判断是否满足堆放条件
        pre_infor = pre_start[0:2] # 前两个元素为底边的长和宽，第3个元素为高
        cur_infro = start[0:2]
        if max(cur_infro)>max(pre_infor) or min(cur_infro) > min(pre_infor): #新堆叠的长方体的底面长和宽（即组合数据中前两个元素中的最大值和最小值，它们分别对应于底面的长和宽），必须分别小于下层长方体的底面的长和宽
            return # 否则，说明不能堆叠，直接返回
        ### 2 更新箱子高度
        if sum + start[2] >self.ways:
            self.ways = sum + start[2]
        ### 3 判断是否终止
        if step >= size:
            return
        #### 4 进入DFS递归
        ###4.1 首先，查看已经访问过的箱子
        new_queue = []
        new_queue.append('*') # 为了保证队列的顺序，提前加入一个元素，待会再删除它
        for qi in queue:
            new_queue.append(qi)
        new_queue.pop(0)
        ###4.2 进入循环
        for i in range(size):
            if i not in new_queue:#如果未曾访问过，则可以访问
                new_queue.append(i)# 加入已访问队列
                for j in range(3):# 依次处理当前箱子的三种情况
                    new_start = new_data[i][j]
                    self.dfs(start,new_start,sum+start[2],step+1,new_queue)
                #### 在进行下一次for循环之前，弹出前一个已访问的箱子，以使得所有箱子均可以作为第二个底层箱子
                new_queue.pop() # 这一步特别重要
        return
## 迎接数据
# 测试用例总数
N = int(input().strip())
data = []
data_size = []
for case in range(N):
    size = int(input().strip())
    data_size.append(size)
    ###
    temp = []
    for di in range(size):
        temp.append(list(map(int,input().strip().split(' '))))
    data.append(temp)
# print(data)
############# 处理 ##############
for case in range(N):
    ### 提取信息
    size = data_size[case]
    subdata = data[case]
    #### 数据处理
    new_data = proData(size,subdata)
    # print(new_data)
    #### DFS 处理 #########
    test = Solution()
    ans = test.DFS()
    #### 打印结果
    print('#'+str(case+1)+' '+str(ans))

输入：

2
2
76 25 3
24 23 4
3
85 20 23
43 18 90
29 12 45

输出：

#1 76
#2 158