大家的人工智能——Logistic回归
在《大家的人工智能——线性回归》中，什么是拟合，代价函数，梯度下降，相信大家已经对这些基本概念有所了解。线性回归的应用场景是输出为连续的数值，比如下个月的房价多少，明天的气温多少。而在机器学习中还有一类任务，它的输出是离散的，比如明天他会不会去游泳（会或不会），这是狗还是猫，这就是分类任务，而Logistic回归就是处理这种分类任务的，不要看他的名字里面有“回归”两个字，但是它其实是个分类算法。它取名Logistic回归主要是因为是从线性回归转变而来的。
二分类
假设我们有一些数据点，我们使用一条直线对这些点进行拟合，这条线称为最佳拟合直线，这个拟合过程称为回归。利用Logistic回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。如下图：
我们想要得到一个函数，能够接收所有的输入然后预测出类别。例如在两个类的情况下，函数输出0或1。该函数称为海维塞德阶跃函数（Heaviside step function），或者直接称为单位阶跃函数。但是海维塞德阶跃函数的问题在于：该函数在跳跃点上从0瞬间跳跃到1，这个瞬间跳跃过程有时很难处理。不过另外一个函数也有类似的性质，而且数学上更容易处理，它就是Sigmoid函数，具体公式如下：
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
Sigmoid函数输入记为z，公式为：
z = w 0 x 0 + w 1 x 1 + w 2 x 2 + ⋅ ⋅ ⋅ + w n x n z = w_0x_0 + w_1x_1 + w_2x_2 + ··· + w_nx_n z=w0x0+w1x1+w2x2+⋅⋅⋅+wnxn
也可以写成向量的形式：
Z = W T X Z = W^TX Z=WTX
Sigmoid函数的形状如下：
Sigmoid函数处处可导，其导数为：
σ ′ ( x ) = σ ( x ) ( 1 − σ ( x ) ) \sigma^{'}(x) = \sigma(x)(1 - \sigma(x)) σ′(x)=σ(x)(1−σ(x))
如下图：
回归函数
我们使用之前线性回归中的参数命名来改写一下上面的方程来得到Logistic回归函数：
h Θ ( X ) = 1 1 + e − Θ T X h_{\Theta}(X) = \frac{1}{1 + e^{-\Theta^TX}} hΘ(X)=1+e−ΘTX1
我们可以看到上面分母中的 Θ T X \Theta^TX ΘTX 与线性回归中的那条“直线”形式一模一样，在Logistic回归中就是要找到一条这样的“直线”进行分类。而上面的h(x)表示属于类别1（二分类）的概率：
h Θ ( X ) = P ( y = 1 ∣ X ; Θ ) h_{\Theta}(X) = P(y = 1 |X;\Theta) hΘ(X)=P(y=1∣X;Θ)
代价函数
我们现在知道在线性回归中的代价函数是什么样的，但是如果将它作为Logistic回归中的代价函数的话，那么它将会是一个非凸函数，会有很多局部最优值，这是因为使用了非线性的sigmoid：
因此在Logistic回归中，我们将使用下面的代价函数：
C o s t ( h Θ ( X ) , y ) = { − l o g ( h Θ ( X ) ) , i f y = 1 − l o g ( 1 − h Θ ( X ) ) , i f y = 0 Cost(h_{\Theta}(X), y) = \left\{ \begin{aligned} -log(h_{\Theta}(X)), \space if \space y = 1 \\ -log(1 - h_{\Theta}(X)) , \space if \space y = 0 \end{aligned}\right. Cost(hΘ(X),y)={−log(hΘ(X)), if y=1−log(1−hΘ(X)), if y=0
那么上面的代价函数为什么是凸函数呢，我们先来看看y=1的情况。
当y=1时，代价函数为-log(h(x)):
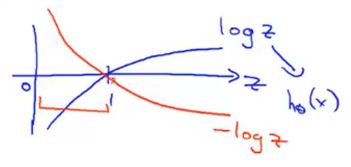
那么为什么是这样的形状呢，我们可以看看log(z)的样子：
红色曲线[0,1]的区间就是y=1时的代价函数。
当y=0时，代价函数为-log(1-h(x)):
把上面的代价函数合起来：
C o s t ( h Θ ( X ) , y ) = − [ y l o g ( h Θ ( X ) ) + ( 1 − y ) l o g ( 1 − h Θ ( X ) ) ] Cost(h_{\Theta}(X), y) = -[ylog(h_{\Theta}(X)) + (1-y)log(1-h_{\Theta}(X))] Cost(hΘ(X),y)=−[ylog(hΘ(X))+(1−y)log(1−hΘ(X))]
那么在所有数据上，代价函数为：
J ( Θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( h Θ ( X ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h Θ ( X ( i ) ) ) ] J(\Theta) = - \frac{1}{m} \sum_{i = 1}^m [y^{(i)}log(h_{\Theta}(X^{(i)})) + (1-y^{(i)})log(1-h_{\Theta}(X^{(i)}))] J(Θ)=−m1i=1∑m[y(i)log(hΘ(X(i)))+(1−y(i))log(1−hΘ(X(i)))]
接下来按照线性回归中提到的方式最小化代价函数即可。
多分类
上面讲述了二分类的情况，现在推广到多分类。但是对于多分类的情况，需要对上面的Logistic进行改进。
- 针对每个类别都建立一个二分类器。
- 修改logistic回归的损失函数，让其考虑每个样本标记的损失，这种方法叫做softmax回归。
回顾一下上面回归函数中，一个样本属于某个类的概率：
h Θ ( X ) = P ( y = k ∣ X ; Θ ) h_{\Theta}(X) = P(y = k |X;\Theta) hΘ(X)=P(y=k∣X;Θ)
将它展开：
h θ ( x ( i ) ) = [ p ( y ( i ) = 1 ∣ x ( i ) ; θ ) p ( y ( i ) = 2 ∣ x ( i ) ; θ ) ⋮ p ( y ( i ) = k ∣ x ( i ) ; θ ) ] = 1 ∑ c = 1 k e θ c T x ( i ) [ e θ 1 T x ( i ) e θ 2 T x ( i ) ⋮ e θ k T x ( i ) ] h_{\theta}(x^{(i)}) = \left[ \begin{matrix} p(y^{(i)} = 1 |x^{(i)};\theta) \\ p(y^{(i)} = 2 |x^{(i)};\theta) \\ ⋮ \\ p(y^{(i)} = k |x^{(i)};\theta) \end{matrix} \right] = \frac{1}{\sum_{c=1}^ke^{\theta_c^Tx^{(i)}}} \left[ \begin{matrix} e^{\theta_1^Tx^{(i)}} \\ e^{\theta_2^Tx^{(i)}} \\ ⋮ \\ e^{\theta_k^Tx^{(i)}} \end{matrix} \right] hθ(x(i))=⎣⎢⎢⎢⎡p(y(i)=1∣x(i);θ)p(y(i)=2∣x(i);θ)⋮p(y(i)=k∣x(i);θ)⎦⎥⎥⎥⎤=∑c=1keθcTx(i)1⎣⎢⎢⎢⎢⎡eθ1Tx(i)eθ2Tx(i)⋮eθkTx(i)⎦⎥⎥⎥⎥⎤
softmax回归代价函数
知道了h(x)的形式之后，我们可以写出它的代价函数：
J ( θ ) = − ∑ i = 1 m ∑ c = 1 k s i g n ( y ( i ) = c ) l o g p ( y ( i ) = c ∣ x ( i ) , θ ) = − ∑ i = 1 m ∑ c = 1 k s i g n ( y ( i ) = c ) l o g e θ c T x ( i ) ∑ l = 1 k e θ l T x ( i ) J(\theta) = -\sum_{i=1}^m\sum_{c=1}^ksign(y^{(i)}=c)logp(y^{(i)} = c|x^{(i)}, \theta) = -\sum_{i=1}^m\sum_{c=1}^ksign(y^{(i)} = c)log\frac{e^{\theta_c^Tx^{(i)}}}{\sum_{l=1}^ke^{\theta_l^Tx^{(i)}}} J(θ)=−i=1∑mc=1∑ksign(y(i)=c)logp(y(i)=c∣x(i),θ)=−i=1∑mc=1∑ksign(y(i)=c)log∑l=1keθlTx(i)eθcTx(i)
其中，如果y=c为真，则sign(y=c)=1，否则为0。
欢迎爱好人工智能的小伙伴关注公众号：机器工匠，不定时发布一些关于人工智能的技术、资讯文章，更有面向初学者的系列文章。
