第一周作业：深度学习基础

一、环境配置
在windows上安装Miniconda+Pycharm+pytorch
参考博客：
https://blog.csdn.net/LLM1602/article/details/105280652
https://blog.csdn.net/suh666888/article/details/107621766
https://blog.csdn.net/m0_37908464/article/details/105832448
二、数据操作
入门
导入torch

使用arange创建一个行向量x，这个行向量包含从0开始的前12个整数，它们被默认创建为浮点数

通过张量的shape属性来访问张量的形状

若只想知道张量中元素的总数

要改变一个张量的形状而不改变元素数量和元素值，可以调用reshape函数

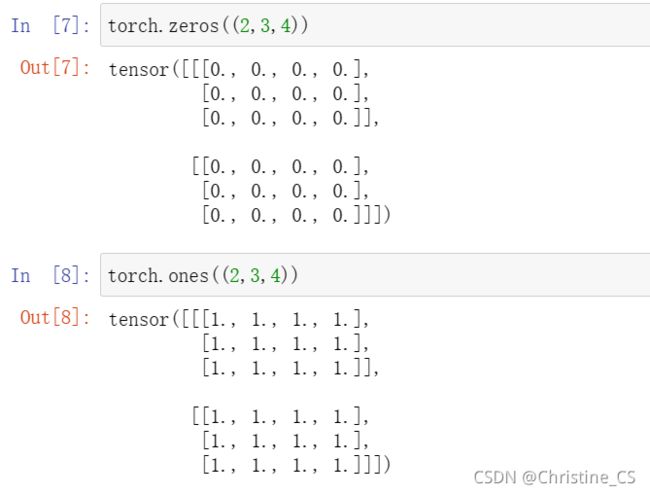
若使用全0、全1、其他常量或者从特定分布中随机采样的数字来初始化矩阵

若想通过从某个特定的概率分布中随机采样来得到张量中每个元素的值（以下代码创建一个形状为（3,4）的张量。其中的每个元素都从均值为0、标准差为1的标准高斯（正态）分布中随机采样）

通过提供包含数值的Python列表（或嵌套列表）来为所需张量中的每个元素赋予确定值

运算


把多个张量连结（concatenate）在一起，把它们端对端地叠起来形成一个更大的张量，只需要提供张量列表，并给出沿哪个轴连结（dim=0为按行连结，dim=1为按列连结）

逻辑语句判断张量对应项是否相同

对张量所有元素求和，得只有一个元素的张量

广播机制

矩阵a将复制列，矩阵b将复制行，然后再按元素相加

索引和切片

节省内存
Python首先计算Y + X，为结果分配新的内存，然后使Y指向内存中的这个新位置，导致结果False

原地操作

如果在后续计算中没有重复使用X，我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销

转换为其他 Python 对象

将大小为1的张量转换为Python标量，可以调用item函数或Python的内置函数

三、数据预处理
读取数据集
将数据集按行写入CSV文件中

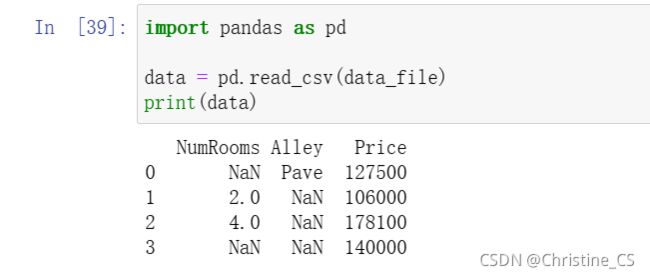
导入pandas包并调用read_csv函数，从csv文件中加载数据集

处理缺失值
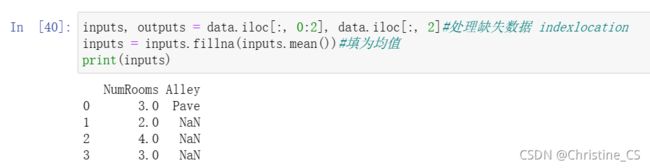
通过位置索引iloc，将data分成inputs和outputs，其中前者为data前两列，后者为data后一列。对于inputs中的缺失值，用同一列的均值替换“NaN”项。

由于Alley列只接受两种类型的类别值“Pave”和“NaN”，pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”，并用0、1标识。

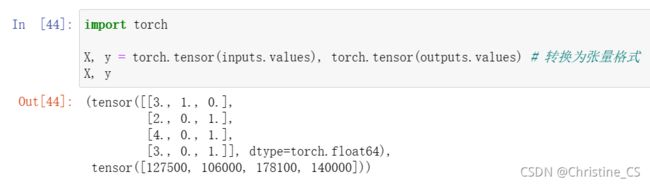
转换为张量格式

四、线性代数
标量
实例化两个标量，并使用它们执行一些熟悉的算术运算，即加法、乘法、除法和指数。

向量
一维张量

通过张量的索引来访问任一元素

长度、维度和形状

矩阵
矩阵与矩阵转置（注：由于torch版本问题，此处计算转置使用A.t()）

对称矩阵的转置与其本身相等

张量
张量是描述具有任意数量轴的 n 维数组的通用方法。

张量算法的基本性质
将两个相同形状的矩阵相加会在这两个矩阵上执行元素加法。

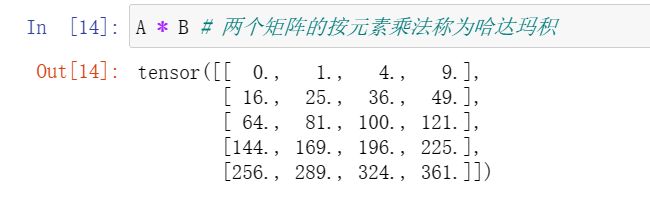
两个矩阵的按元素乘法称为哈达玛积。

将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

降维
默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。

指定dim=1（0）将通过汇总所有列（行）的元素降维。（注：由于torch版本问题，此处轴替换axis使用dim表示）

沿着行和列对矩阵求和，等价于对矩阵的所有元素进行求和。

将总和除以元素总数来计算平均值，计算平均值的函数也可以沿指定轴降低张量的维度。

非降维求和
在调用函数来计算总和或均值时保持轴数不变

调用cumsum函数，求沿某个轴计算A元素的累积总和。

点积
给定两个向量x，y∈Rᵈ，它们的点积x^T~y（或）是相同位置的按元素乘积的和：

可以通过执行按元素乘法，然后进行求和来表示两个向量的点积

矩阵-向量积
当我们为矩阵A和向量x调用np.dot(A,x)时，会执行矩阵-向量积。注意，A的列维数（沿轴1的长度）必须与x的维数（其长度）相同。

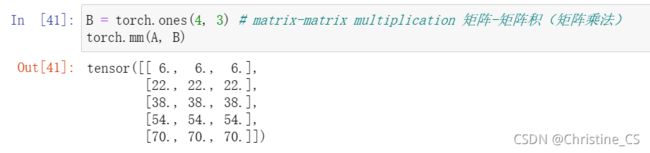
矩阵-矩阵乘法
我们可以将矩阵-矩阵乘法 AB 看作是简单地执行 m 次矩阵-向量积，并将结果拼接在一起，形成一个 n×m 矩阵。

范数
L₁ 范数和 L₂ 范数都是更一般的 L_p范数的特例：

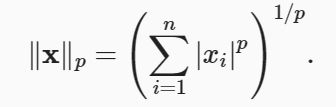
L₂ 范数：假设 n 维向量 x 中的元素是 x₁,…,x _n，其 L₂ 范数是向量元素平方和的平方根：


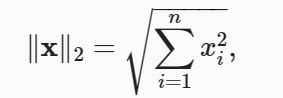
L₁范数：与 L₂ 范数相比受异常值的影响较小，它表示为向量元素的绝对值之和：


类似于向量的 L₂ 范数，矩阵 X∈R^m×n 的弗罗贝尼乌斯范数（Frobenius norm）是矩阵元素平方和的平方根：

五、矩阵计算
标量导数

亚导数


梯度

y是标量，x是列向量，y对x求导后结果为行向量。



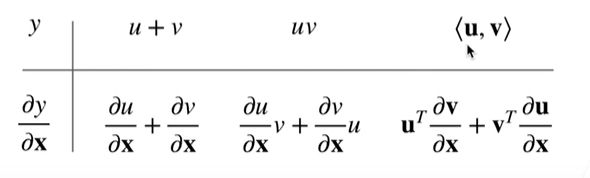
y是列向量，x是标量，y对x求导后结果为列向量。

y是列向量，x是列向量，y对x求导后结果为矩阵。

样例


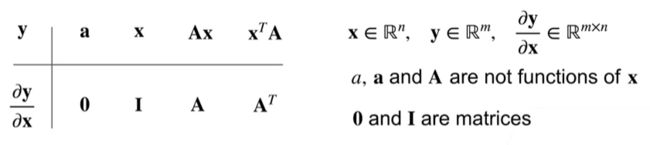
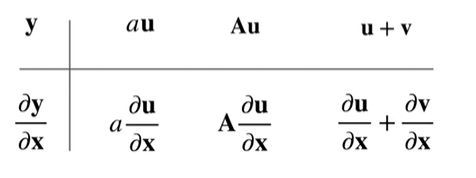
六、自动求导
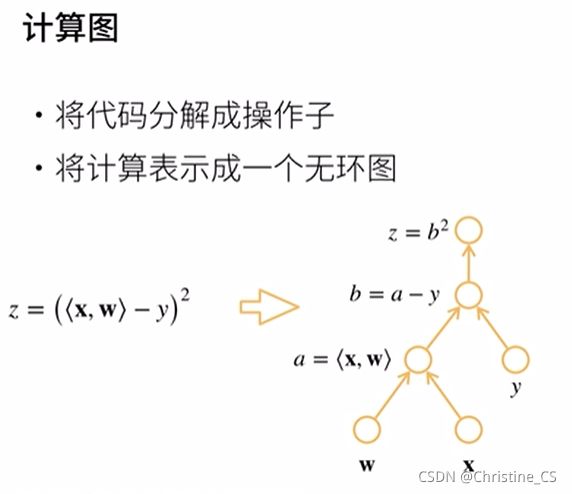
链式求导



自动求导
计算一个函数在指定值上的导数，与符号求导和数值求导不同。






自动求导实现
在我们计算 y 关于 x 的梯度之前，我们需要一个地方来存储梯度（x.grad）。

计算y（隐式构造计算图，有grad_fn函数保存在此处）

通过调用反向传播函数来自动计算y关于x每个分量的梯度，打印这些梯度；并验证计算正确性。

求另一个函数的梯度之前用zero_()清零。

非标量变量的反向传播
深度学习中，我们的目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和。

分离计算
将某些计算移动到记录的计算图之外
下面的反向传播函数计算z=ux关于x的偏导数，同时将u作为常数处理，而不是z=xxx关于x的偏导数。
detach():阻断反向传播，u不再是关于x的函数，而是常数，值为xx。

Python控制流的梯度计算
构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度。

问题
矩阵计算中，在标量对向量、向量对标量、向量对向量求梯度的问题上，仍需要多揣摩多计算。
自动求导中，分离计算中detach()函数的作用起初没有理解，搜索后明白了，但对其使用场景仍无概念，需要进一步学习。

感想
深度学习第一周，安装环境，学习基础数据操作、数据预处理、线性代数自动求导等数学知识。在安装环境上就遇到不少困难，包括对虚拟环境、指令的不熟悉等等，很感谢网络上丰富的资源帮助我解决每一个问题；学习部分，李沐老师视频课程讲解很精炼细致，每一句都不容错过，结合代码体会每一个函数、每一次操作的用意，对于加深理解大有裨益。今后要养成整理笔记的习惯，通篇整理下来，对前几天的学习内容有了更系统的感知，对于一些细节问题也好查漏补缺。