论文精读-基于双目图像的视差估计方法研究以及实现
基于双目图像的视差估计方法研究及实现
- 第一章 绪论
-
- 1.1 课题的研究背景与意义
- 1.2 双目视差估计的研究现状
-
- 1.2.1 传统立体匹配方法研究现状
- 1.2.2 统计学习方法研究现状
- 1.2.3 深度学习方法研究现状
第一章 绪论
1.1 课题的研究背景与意义
侵权删,请联系。
1、最早出现的非接触测量技术:基于红外光、超声波、雷达等非光学仪器
原理:仪器主动发出信号,利用收到回波的时间来计算距离。
假设光速为V,传播时间为T,距离为S = VT/2
2、光学图像测距:单目测距和双目测距
单目测距:利用翻个摄像头拍摄的图片来还原场景的三维信息。
原理:利用遮挡、近大远小等先验信息来计算距离
缺点:在没有一个标准的参考下很难实现,缺乏可移植性。
双目测距:模拟人眼判断事物距离的机制,使用放在同一水平线上的两部相机同时或许图像,利用同一物体在两幅图像中位置差异来获取视差图。
3、两大标准立体数据集:KITTI、Middlebury
(1)自动驾驶KITTI数据集详解
KITTI是目前自动驾驶领域最重要的测试集之一,它可以提供大量的真实场景的数据集,用来更好的度量和测试算法的表现。
下面介绍KITTI的几项benchmark
stereo
stereo Evaluation(立体评估)
基于图像的立体视觉和三维重建,一般从不同角度的多张图片来恢复三维结构。
可还原:物体的形状、周围环境的形状的。
stereo与depth的区别:
stereo侧重于场景中的立体对象,depth侧重于场景中距离的远近。而depth信息可能还需要依赖于stereo信息,不然整个图像就只能得到平面的深度信息,而不是三维的深度信息。
Flow
Optical Flow Evaluation 光流
光流是关于视域中的物体运动检测中的概念。用来描述相对于观察着的运动所造成的观测目标、表面或边缘的运动。
应用领域:运动检测、对象分割,接触时间信息,扩展计算焦点,亮度、运动补偿编码、立体视差测量。
原理:通过检测图像像素点的强度随时间的变化而推断出物体的移动速度以及方向的方法
方法:相位相关、基于块的方法、离散优化方法
微分估计黄牛的方法(
Lucas - Kanade method
Horn - Schunck
Buxton - Jepson method
General variational methods)
相关研究:
little-rocket:Oprical Flow 介绍与代码实现:https://zhuanlan.zhihu.com/p/44859953
光流Optical Flow 介绍与Opencv实现:https://link.zhihu.com/?target=https%3A//blog.csdn.net/zouxy09/article/details/8683859
林天威:【CVPR2018论文笔记】光流与行为识别的结合研究:https://zhuanlan.zhihu.com/p/32443212
Sceneflow
Scene Flow 场景流
场景流是场景的密集或半密集3D运动场,就是光流的三维版本,表述了图像/点云中每个点在前后两帧的变化情况。其相对于相机完全部分的移动.
应用:
机器人技术中,用于需要预测周围物体的运动的动态环境中的自主导航或操纵。
补充和改进最先进的视觉测距和SLAM算法,这些算法通常假设在刚性或准刚性环境中工作。
用于机器人或人机交互、虚拟和增强现实。
场景流相对光流的区别:
光流是平面运动的二维信息,场景流包括了空间中物体运动的三维信息。
Depth
depth Evaluation 深度
视觉深度估计。视觉深度在视觉SLAM和里程计方面应用广泛,深度信息的获取可以参考stereo的方法。
应用:其中如果是基于视觉的odometry,那么就需要用到视觉depth evaluation技术。其中包括2项benchmark、深度补全和深度预测(The depth completion and depth prediction)
odometry
Visual Odometry / SLAM Evaluation 2012 里程计
视觉里程计,需要用到depth evaluation 技术。
用到了下面集中方法:
stereo:立体成像
Laser Points:使用来自Velodyne激光雷达点云的方法
Loop Closure Detection:一种检测循环闭包的SLAM方法
Additional training tada:使用其他数据源进行训练
可以看到这项benchmark有视觉的和Lidar激光雷达的传感器方案,并且引入SLAM方法中的闭环检测。
object
Object Tracking Evaluation 2012 物体追踪
3D物体追踪,主要是针对汽车和行人的目标追踪。由于没有单一的评估标准,没有对方法做排名。上面介绍的光流和场景流广泛应用在物体追踪上面。
Road
Road/Lane Detection Evaluation 2013 车道线识别
车道线识别,车道线识别是无人驾驶很基础的功能,而且是ADAS中车道线保持等功能的前提,所以车道线的benchmark至关重要。
问题:车道线不完整的情况如何处理?下雨反光或者夜间的时候如何处理,不知道数据集是否有覆盖。

引用Robust Lane Detection from Continuous DrivingScenes Using Deep Neural Networks
它包含三种不同类别的道路场景:
Uu - 城市无标记(98/100)
Um - 城市标记(95/96)
Umm - 城市多重标记车道(96/94)
Urban - 上述三者的结合
Semantics
Smantic and Instance Segmenttation Evaluation 场景分割
语义和实例分割评估,语义分割对无人驾驶的处理很关键,比如人会根据语义处理,区分车道周围的环境以及汽车,然后对不同的场景做处理。如果没有语义处理,所有的像素将会同等对待,对处理和识别都会引入干扰。

任务侧重于检测,分割和分类对象实例。其中有像素级的分割和实例级别的分割。
补充:超像素、语义分割、实例分割、实景分割
superpoxels超像素
第一次听说这个超像素很容易理解错误,以为是在普通像素的基础上继续微观细分,如果这样理解就恰好相反了。其实超像素是一系列像素的集合,这些像素具有类似的颜色,纹理等特征,距离也比较近。用超像素对一张图片进行分割的结果如下图,**其中每个白色线条区域内的像素集合就是一个超像素。**需要注意的是,超像素很可能把同一个物体的不同部分分成多个超像素。

Segmantic Segmentation 语义分割
语义分割还是比较常见的。就是把图像中每个像素赋予一个类别标签(比如汽车,建筑,地面等),然后赋予不同的颜色。
缺点:如果一个像素被标记为红色,那就代表整个像素所在的位置是一个人,但如果有两个都是红色的像素,这种方式无法判断它们是属于同一个人还是不同的人。也就是说,语义分割只能判断类别,无法区别个体。

但很多时候我们更需要个体信息,想要区分个体怎么办,继续往下看。
Instance Segmentation 实例分割
实例分割方式有点类似于物体检测,不过物体检测一般输出的是bounding box,实例分割输出的是一个mask。
实例分割和上面的语义分割也不同,它不需要对每个像素进行标记,它只需要找到感兴趣的物体的边缘轮廓就行。比如下图中的人就是感兴趣的物体。该图的分割方法采用了一种称为Mask R - CNN 的方法。我们可以看到每个人都是不同的颜色轮廓,因此我们可以区分单个个体。

Panoptic Segmentation 全景分割
全景分割是语义分割和实例分割的结合。如下图,每个像素都被分为一类,如果一种类别中有多个实例,会用不同的颜色区分,我们可以知道哪个像素属于哪个类中的哪个实例。比如下图中的黄色和红色都属于人这一个类别李,但是分别属于不同的实例(人),因此我们可以通过mask的颜色很容易分辨出不同的实例。
**KITTI 领域 论文代码的实现:**https://link.zhihu.com/?target=https%3A//paperswithcode.com/sota
(2) Middlebury立体视觉数据集
Middlebury 权威立体视觉测评网站。该网站和测试数据集一直被广泛使用。它提供了许多标准的测试库,以及最新的匹配算法性能情况。
Computer Vision Toolkit (cvkit) 是发布在 Middlebury Stereo Datasets 上的一套计算机视觉研究工具集。本文主要记录它的安装和使用方法。可查看:RGB、Disparity图像、点云图,点云处理。将深度图转为ply,详情见:
https://blog.csdn.net/RadiantJeral/article/details/86008558
4、双目深度估计算法普遍适用的框架:匹配代价计算、匹配代价聚合、视差计算及优化和视差精细化
(1)匹配代价计算
匹配代价计算就是衡量像素之间的相似程度,当代价越大,左右图像的像素点就越不像似。
常用匹配代价:AD、SSD、SAD、Census、NCC,BT,MI,LOG等
AD
AD变换反映的是像素点的灰度变化,在纹理丰富区域有良好的匹配效果,是一种简单的、易实现的代价衡量方法。但是,基于单个像素点计算的匹配代价往往会收到图像噪声,光照不均等的影像,相似度可靠性不高。
——颜色差异的绝对值

C为匹配代价,p为某个像素点,d为视差,n为图像通道数,I为对应通道的灰度值,i 为 通道
——梯度差异的绝对值

SAD
SAD(sum of absolute difference)为像素领域内对应位置灰度差的绝对值之和,可以很容易的嵌入到FPGA公式中,实现实时,但是两幅图像的灰度值易受光照影响。
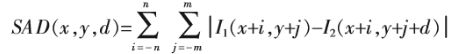
SSD
SSD(Sum of Squared Difference)为像素差的平方和,相对于SAD具有更高的复杂度,因为有乘法操作。同时,SAD更加鲁棒,SSD易受噪声影响。

注意:SAD和SSD都直接利用图像的灰度信息值,所以对光照的变化十分敏感,其次,采用的领域窗口为矩形,对于旋转和缩放比较铭感,当发生较大尺度的旋转和尺度缩放时,窗口内的点将发生较大变换。
相关拓展请看特征点检测内容:
特征点检测的描述子需要旋转一致性,检测子需要尺度一致性。通俗点说,就是如果不具备旋转不变性的话,你有个相机相对地面拍摄角度,与另一个相机不一样的话,拍出来的照片是斜的,然后虽然东西还是那个东西,但特征检测的时候就不认识了。而尺度一致性就是个远近拍摄的事情,远处拍完也可能检测不出来。
检测子和描述子的关系:
检测子就是按照灰度特征检测出来的特征点,比如说角点。也有自己设计的特征让图片检测的,比如SURF、SIFT、ORB,就是安排一个规律,让符合这个规律的点检测出来,而描述子就相当于给监测点做个存在一定特性的编码,用这个编码去匹配各个检测子。一般的算法都是这个套路,主要是看检测子的能力问题。
也就是说,就是说,像SIFT之类的算法,有点类似于战争时期的电码,自己制作一套规律,再从图片中提取符合这个规律的点称为检测点,描述子就相当于一个代号,编号,一遍两张图匹配的时候对号入座。
NCC
NCC:归一化互相关系数(归一化:消除对光照敏感的问题),对不同光照强度更加鲁棒,但复杂程度更高,仍采用的时矩形窗口,对旋转和尺度变换敏感。
Census变换
Census变换是在图像区域定义一个矩形窗口,用这个窗口遍历整幅图像。选取中心像素作为参考像素,将矩形窗口中每个像素的灰度值与参考像素的灰度值进行比较,灰度值小于或等于参考值的像素标记为0,大于参考值的像素标记为1,最后将它们按位连接,得到变换后的结果,变换后的结果是由0和1组成的二进制码流。如图下:


Census 变换的匹配代价计算方法是计算左右图像中对应的两个像素的Census变换值的汉明距离(Hamming )
汉明距离:在二进制编码中,表示两个相同长度的字对应位不同的数量。

——优点:
Census 变换对图像的明暗变化不敏感,能够容忍一定的噪声,因为比较的是相对灰度关系,所以即使左右影响亮度不一致,也能得到较好的匹配效果。而且,相比互信息具有并行度高的优点。Census变换值是局部窗口运算,每个像素都可以独立运算,这个特性让其可以很好的设计多线程并行计算模型,无论是CPU并行还是GPU并行,都能达到较高的并行效率。
BT
BT 方法主要是解决图像深度不连续的问题

BT方法(Birchfield和Tomasi的方法)
立体匹配SGBM算法
Opencv源代码分析-SGBM
MI
信息量
信息量是指信息多少的量度,举个简单的例子,以下两个句子,哪一个句子的信息量更大呢?
我今天没中彩票
我今天中彩票了
从文本上来看,这两句话的字数一致,描述的事件也基本一致,但是显然第二句话的信息量要比第一句大得多,原因也很简单,因为中彩票的概率要比不中彩票低得多。一个信息传递的事件发生的概率越低,它的信息量越大。用一个函数来描述信息量需要满足如下条件:
信息量是指信息多少的量度,举个简单的例子,以下两个句子,哪一个句子的信息量更大呢?
我今天没中彩票
我今天中彩票了
从文本上来看,这两句话的字数一致,描述的事件也基本一致,但是显然第二句话的信息量要比第一句大得多,原因也很简单,因为中彩票的概率要比不中彩票低得多。一个信息传递的事件发生的概率越低,它的信息量越大。用一个函数来描述信息量需要满足如下条件:

满足上述条件的函数是对数函数,因此我们用对数函数来量化一个事件的信息量:

信息熵
在信息论中,熵是接受的每条信息中包含的平均量(用期望来表示),熵的单位通常位比特,但也用Sh、nat、Hart计量,取决于定义用到的对数底。
连续的:

离散的:

互信息
两个随机变量的互信息(Mutual Information)是两个变量相互依赖的度量:单独考虑两个变量、总和考虑两个变量,如果这两种情况导致的结果差别很大,则他们的关系不浅。

互信息与熵的关系:在给定Y的条件下,X的不确定度的缩减量

![]()
1.H(Y):随机变量Y不确定度的量度
2.H(Y|X):随机变量X没有涉及到的随机变量Y的部分的不确定度的量度,也就是”在X已知之后Y的剩余不确定度的量“
3.H(Y) - H(Y|X):Y的不确定度,减去在X已知之后的Y的剩余不确定度的量,等价于:移除知道X后,Y的不确定度的量。
公式推导:

组合代价:AD-Census

(2)匹配代价聚合
因为局部算法在计算代价时,只考虑了局部的信息,在特征明显的地方能够匹配的较好,但在一些噪声大的边缘区域往往难以匹配,所以采用代价聚合的方法,每个像素在某个视差下的信贷加值都会根据其相邻像素在同一视差值或附近视差下的代价值来重新计算,得到新的代价值,用矩阵S来表示。这是基于同一深度的像素又相同的视差值的先验知识。
代价聚合也可以理解为视差的传播,让信噪比高的区域的视差传播到信噪比低的区域,使得所有点的代价都能较好的表示真实的相关性。
常用的方法:扫描线法,动态规划法,SGM算法中的路径聚合法。
全局匹配算法:
全局匹配主要是利用图像的全局约束信息,通过构建全局能量函数,然后通过优化方法最小化全局能量函数以求得致密的视差图。目前优化方法主要有:动态规划(DP)、置信传播(BP)、模拟退火、图割法(GC)等。
动态规划:
动态规划的思想就是把求解整个过程分解为若干子过程,逐步求解子过程。
学习动态规划相关知识的链接:
https://www.bilibili.com/video/av16544031/?spm_id_from=333.788.videocard.1
https://www.bilibili.com/video/av45990457?from=search&seid=5131266338769155396

在双目匹配中,动态规划立体匹配是基于极限约束,通过依次寻找每条极线上匹配点对的最小代价路径的动态寻优方法求解全局能量最小化,得到匹配视差图。
步骤如下:

step2. 代价函数构建
代价函数构建这里采用的是块匹配,也就是第一图像待匹配点为中心像素创建一个nn的窗口,在第二幅图像中,沿着极线取出与基准点邻域同样大小为nn的邻域,进行邻域内的相似度函数的计算。
说明:代价函数采用的是C++中的继承构建
——image Type:判断左右图像的信息相似性。比如大小是否一样大。
——aggregate:这就是所谓的代价聚合函数,计算左右图像领域内的相似性度量的。
class CostFunction {
public:
float lambda;
cv::Mat left;//左图像
cv::Mat right;//右图像
int blocksize;//block大小
int margin;//块的边界
float normCost;
float normWin;
//构造函数
CostFunction( cv::Mat left, cv::Mat right, float lambda)
{
lambda = 1.0;
this->left = left;
this->right = right;
imageType(left, right);
this->lambda = lambda;
}
//虚构函数
virtual bool imageType(cv::Mat left, cv::Mat right) {
assert(left.size() == right.size());
return true;
}
//代价聚合
virtual float aggregate(int x1, int x2, int y) = 0;
float p(float cost) {
return 1 - exp(-cost / lambda);
}
~CostFunction() {}
};
class RGBCost : public CostFunction {
public:
RGBCost(cv::Mat left, cv::Mat right, float lambda) : CostFunction(left, right, lambda) {}
bool imageType(cv::Mat left, cv::Mat right) {
assert(left.type() == right.type() && "imgL imgR types not equal");
assert(left.type() == CV_8UC3 && "img type not supported");
return true;
}
// aggregate over a ROI of input images
float aggregate(int x1, int x2, int y) {
float sum = 0;
for (int i = y - margin; i <= y + margin; ++i) {
cv::Vec3b* lptr = left.ptr<cv::Vec3b>(i);
cv::Vec3b* rptr = right.ptr<cv::Vec3b>(i);
for ( int j = -margin; j <= margin; ++j) {
sum += eukl(lptr[x1 + j], rptr[x2 + j]); // cost function
}
}
return sum / sqrt(255*255 + 255*255+255*255); // normalize to winsize*1.0
}
float eukl(cv::Vec3b l, cv::Vec3b r) {
float a = l[0] - r[0];
float b = l[1] - r[1];
float c = l[2] - r[2];
return std::sqrt(a*a + b*b + c*c);
}
~RGBCost() {}
};
class FloatCost : public CostFunction {
public:
FloatCost(cv::Mat left, cv::Mat right, float lambda) : CostFunction(left, right, lambda) {}
bool imageType(cv::Mat left, cv::Mat right) {
assert(left.type() == right.type() && "imgL imgR types not equal");
assert(left.type() == CV_32F && "img type not supported");
return true;
}
// aggregate over a ROI of input images
float aggregate(int x1, int x2, int y) {
float sum = 0;
for (int i = y - margin; i <= y + margin; ++i) {
float* lptr = left.ptr<float>(i);
float* rptr = right.ptr<float>(i);
for ( int j = -margin ; j <= margin; ++j) {
sum += abs(lptr[x1 + j] - rptr[x2 + j]); // cost function
}
}
return sum / (blocksize*blocksize*lambda);
}
};
class CondHistCost : public CostFunction {
public:
cv::Mat nuLeft, nuRight;
CondHistCost(cv::Mat left, cv::Mat right, float lambda) : CostFunction(left, right, lambda) {
cv::Mat histl = condHist(left, 3);
nuLeft = switchColors(left, histl);
cv::Mat histr = condHist(right, 3);
nuRight = switchColors(right, histr);
}
bool imageType(cv::Mat left, cv::Mat right) {
assert(left.type() == right.type() && "imgL imgR types not equal");
assert(left.type() == CV_32F && "img type not supported");
return true;
}
// aggregate over a ROI of input images
float aggregate(int x1, int x2, int y) {
float sum = 0;
for (int i = y - margin; i <= y + margin; ++i) {
float* lptr = nuLeft.ptr<float>(i);
float* rptr = nuRight.ptr<float>(i);
for ( int j = -margin ; j <= margin; ++j) {
sum += abs(lptr[x1 + j] - rptr[x2 + j]); // cost function
}
}
return sum / (blocksize*blocksize*lambda);
}
};
class GrayCost : public CostFunction {
public:
GrayCost(cv::Mat left, cv::Mat right, float lambda) : CostFunction(left, right, lambda) {}
bool imageType(cv::Mat left, cv::Mat right) {
assert(left.type() == right.type() && "imgL imgR types not equal");
assert(left.type() == CV_8UC1 && "img type not supported");
return true;
}
// aggregate over a ROI of input images
float aggregate(int x1, int x2, int y) {
float sum = 0;
for (int i = y - margin; i <= y + margin; ++i) {
uchar* lptr = left.ptr<uchar>(i);
uchar* rptr = right.ptr<uchar>(i);
for ( int j = -margin; j <= margin; ++j) {
sum += abs(lptr[x1 + j] - rptr[x2 + j]); // cost function
}
}
return sum / (blocksize*blocksize*255.0);
}
};
class GradientCost : public CostFunction {
public:
cv::Mat l_grad; // 3 channel float
cv::Mat r_grad; // 3 channel float
GradientCost(const cv::Mat left, const cv::Mat right, float lambda) : CostFunction(left, right, lambda) {
l_grad = getRGBGradientAngle(left);
r_grad = getRGBGradientAngle(right);
//displayGradientPic(l_grad);
//displayGradientPic(r_grad);
}
bool imageType(cv::Mat left, cv::Mat right) {
assert(left.type() == right.type() && "imgL imgR types not equal");
assert(left.type() == CV_8UC3 && "img type not supported");
return true;
}
// aggregate over a ROI of input images
float aggregate(int x1, int x2, int y) {
float sum = 0;
for (int i = y - margin; i <= y + margin; ++i) {
cv::Vec3f* lptr = l_grad.ptr<cv::Vec3f>(i);
cv::Vec3f* rptr = r_grad.ptr<cv::Vec3f>(i);
for ( int j = -margin; j <= margin; ++j) {
sum += eukl(lptr[x1 + j], rptr[x2 + j]); // cost function
}
}
return sum / sqrt(255*255 + 255*255 + 255*255); // normalize to winSize * 1.0
}
float eukl(cv::Vec3f l, cv::Vec3f r) {
float a = l[0] - r[0];
float b = l[1] - r[1];
float c = l[2] - r[2];
return std::sqrt(a*a + b*b + c*c);
}
~GradientCost() {
l_grad.release();
r_grad.release();
}
};
class CensusCost : public CostFunction {
public:
int censusWindow;
int censusMargin;
CensusCost(cv::Mat left, cv::Mat right, int censusWindow, float lambda) : CostFunction(left, right, lambda) {
// census.... nimmt einen Block
this->censusWindow = censusWindow;
this->censusMargin = censusWindow / 2;
this->normWin = censusWindow * censusWindow;
// nimmt einen Block
}
bool imageType(cv::Mat left, cv::Mat right) {
assert(left.type() == right.type() && "imgL imgR types not equal");
assert(left.type() == CV_8UC1 && "img type not supported");
return true;
}
unsigned int census(int x1, int x2, int y, uchar c1, uchar c2) {
unsigned int diff = 0;
for(int i = y - censusMargin; i <= y + censusMargin; ++i) {
uchar* lptr = left.ptr<uchar>(i);
uchar* rptr = right.ptr<uchar>(i);
for(int j = -censusMargin; j <= censusMargin; ++j) {
bool t1 = (c1 < lptr[x1 + j]);
bool t2 = (c2 < rptr[x2 + j]);
if(t1 != t2) diff++;
}
}
return diff; /// (censusWindow*censusWindow);
}
float aggregate(int x1, int x2, int y) {
float sum = 0;
/*for(int i = y - margin; i <= y + margin; ++i) {
uchar *lptr = left.ptr(i);
uchar *rptr = right.ptr(i);
for(int j = -margin; j <= margin; ++j)
sum += census(x1 + j, x2 + j, i, lptr[x1 + j], rptr[x2 + j]);
}*/
uchar *lptr = left.ptr<uchar>(y);
uchar *rptr = right.ptr<uchar>(y);
sum = census(x1, x2, y, lptr[x1], rptr[x2]);
return sum / normWin;
}
};
class CensusFloatCost : public CostFunction {
public:
int censusWindow;
int censusMargin;
CensusFloatCost(cv::Mat left, cv::Mat right, int censusWindow, float lambda) : CostFunction(left, right, lambda) {
// census.... nimmt einen Block
this->censusWindow = censusWindow;
this->censusMargin = censusWindow / 2;
}
bool imageType(cv::Mat left, cv::Mat right) {
assert(left.type() == right.type() && "imgL imgR types not equal");
assert(left.type() == CV_32F && "img type not supported");
return true;
}
unsigned int census(int x1, int x2, int y, float c1, float c2) {
unsigned int diff = 0;
for(int i = y - censusMargin; i <= y + censusMargin; ++i) {
float* lptr = left.ptr<float>(i);
float* rptr = right.ptr<float>(i);
for(int j = -censusMargin; j <= censusMargin; ++j) {
bool t1 = (c1 < lptr[x1 + j]);
bool t2 = (c2 < rptr[x2 + j]);
if(t1 != t2) diff++;
}
}
return diff;
}
float aggregate(int x1, int x2, int y) {
float sum = 0;
for(int i = y - margin; i <= y + margin; ++i) {
float *lptr = left.ptr<float>(i);
float *rptr = right.ptr<float>(i);
for(int j = -margin; j <= margin; ++j)
sum += census(x1 + j, x2 + j, i, lptr[x1 + j], rptr[x2 + j]);
}
float *lptr = left.ptr<float>(y);
float *rptr = right.ptr<float>(y);
//sum = census(x1, x2, y, lptr[x1], rptr[x2]);
return sum / (censusWindow*censusWindow*lambda);
}
};
class RGBCensusCost : public CostFunction {
public:
int censusWindow;
int censusMargin;
RGBCensusCost(cv::Mat left, cv::Mat right, int censusWindow, float lambda) : CostFunction(left, right, lambda) {
// census.... nimmt einen Block
this->censusWindow = censusWindow;
this->censusMargin = censusWindow / 2;
normCost = censusWindow*censusWindow*3;
// nimmt einen Block
}
bool imageType(cv::Mat left, cv::Mat right) {
assert(left.type() == right.type() && "imgL imgR types not equal");
assert(left.type() == CV_8UC3 && "img type not supported");
return true;
}
unsigned int census(int x1, int x2, int y, cv::Vec3b c1, cv::Vec3b c2) {
unsigned int diff = 0;
for(int i = y - censusMargin; i <= y + censusMargin; ++i) {
cv::Vec3b* lptr = left.ptr<cv::Vec3b>(i);
cv::Vec3b* rptr = right.ptr<cv::Vec3b>(i);
for(int j = -censusMargin; j <= censusMargin; ++j) {
cv::Vec3b cl = lptr[x1 + j];
cv::Vec3b cr = rptr[x2 + j];
for(int ch = 0; ch < 3; ++ch) {
bool t1 = (c1[ch] < cl[ch]);
bool t2 = (c2[ch] < cr[ch]);
if(t1 != t2) diff++;
}
}
}
return diff;
}
float aggregate(int x1, int x2, int y) {
float sum = 0;
for(int i = y - margin; i <= y + margin; ++i) {
cv::Vec3b *lptr = left.ptr<cv::Vec3b>(i);
cv::Vec3b *rptr = right.ptr<cv::Vec3b>(i);
for(int j = -margin; j <= margin; ++j)
sum += census(x1 + j, x2 + j, i, lptr[x1 + j], rptr[x2 + j]);
}
//cv::Vec3b *lptr = left.ptr(y);
//cv::Vec3b *rptr = right.ptr(y);
return sum / normCost;
}
};
class RGBGradCensusCost : public CostFunction {
public:
int censusWindow;
int censusMargin;
float normCost;
float normWin;
cv::Mat l_grad;
cv::Mat r_grad;
RGBGradCensusCost(cv::Mat left, cv::Mat right, int censusWindow, float lambda) : CostFunction(left, right, lambda) {
// census.... nimmt einen Block
this->censusWindow = censusWindow;
this->censusMargin = censusWindow / 2;
normWin = censusWindow*censusWindow*3;
// nimmt einen Block
l_grad = getRGBGradientAngle(left);
r_grad = getRGBGradientAngle(right);
}
bool imageType(cv::Mat left, cv::Mat right) {
assert(left.type() == right.type() && "imgL imgR types not equal");
assert(left.type() == CV_8UC3 && "img type not supported");
return true;
}
unsigned int census(int x1, int x2, int y, cv::Vec3f c1, cv::Vec3f c2) {
unsigned int diff = 0;
for(int i = y - censusMargin; i <= y + censusMargin; ++i) {
cv::Vec3f* lptr = l_grad.ptr<cv::Vec3f>(i);
cv::Vec3f* rptr = r_grad.ptr<cv::Vec3f>(i);
for(int j = -censusMargin; j <= censusMargin; ++j) {
cv::Vec3f cl = lptr[x1 + j];
cv::Vec3f cr = rptr[x2 + j];
for(int ch = 0; ch < 3; ++ch) {
bool t1 = (c1[ch] < cl[ch]);
bool t2 = (c2[ch] < cr[ch]);
if(t1 != t2) diff++;
}
}
}
return diff;
}
float aggregate(int x1, int x2, int y) {
float sum = 0;
/*for(int i = y - margin; i <= y + margin; ++i) {
cv::Vec3f *lptr = l_grad.ptr(i);
cv::Vec3f *rptr = r_grad.ptr(i);
for(int j = -margin; j <= margin; ++j)
sum += census(x1 + j, x2 + j, i, lptr[x1 + j], rptr[x2 + j]);
}*/
cv::Vec3f *lptr = l_grad.ptr<cv::Vec3f>(y);
cv::Vec3f *rptr = r_grad.ptr<cv::Vec3f>(y);
sum = census(x1, x2, y, lptr[x1], rptr[x2]);
return sum / normWin;
}
};
step3. 视差空间的构建

DSI(Disparity Space Image)视差空间图像为一个三维矩阵,主要右横轴x,纵轴y,视差搜索范围d构成,传统的DP方法一般就是为了在某固定的Y(也就是某条极限上)寻找一条从最左段到最右段的最小代价路径,每条路径的代价为
![]()
——视差空间的构建
输入参数:
——imageSize:图像的大小
——blocksize块的大小
——y:某条极线
输出参数:
——map :某极线上左右图像两两邻域相互的代价值
——左范围:[margin, imageSize.width - margin]
——右范围:[margin, imageSize,width - margin]
cv::Mat BlockMatching::disparitySpace(Size imageSize, int blocksize, int y)
{
int margin = blocksize / 2;
int start = margin;
int stopW = imageSize.width - margin;
int workSpace = stopW - start;
// leave out the borders
//Mat map = Mat(workSpace, workSpace, CV_32F); // not preinitialized.. // numeric_limits::max());
Mat map = Mat(workSpace, workSpace, CV_32F, numeric_limits<float>::max());
//int dmax = 101;
for(int x1 = start; x1 < stopW; x1++) {
float* ptr = map.ptr<float>(x1 - margin); // [x1 - margin, x2 - margin]
//ptr[max(x1 - 1, start) - margin] = numeric_limits::max(); // fast borders
//ptr[min(x1 + dmax, stopW - 1) - margin] = numeric_limits::max();
//for(int x2 = x1; x2 < min(x1 + dmax, stopW); x2++) {
for(int x2 = start; x2 < stopW; x2++) {
// combine costs
float cost = 0;
for(size_t i = 0; i < functions.size(); ++i) {
float val = functions[i]->aggregate(x1, x2, y);
mins[i] = min(mins[i], val); // debug
maxs[i] = max(maxs[i], val); // debug
cost += val;
}
// x1, x2. Das heißt x1 sind die Zeilen. Wir gehen jedes Mal die Zeilen runter.
// geht nur von 0 - workspace, deshalb margin abziehen
//map.at(x1 - margin, x2 - margin) = greySad(leftRoi, rightRoi);
ptr[x2 - margin] = cost;
}
}
return map;
}
step4: 动态规划
主要分为四步:
1、设置初始位置的值(已知的值,这里设置的最后一行,最后一列为初始值)
2、计算边界上的代价(最后一行,最后一列)
3、从三个方向(向上,向左,斜向上)计算代价
4、记录每一步的方向
5、第一行的最小值即为视差点


最小路径和代码
int minPathSum1(int matrix[][col], int dp[][col], int path[][col])
{
if(matrix == NULL)
{
return 0;
}
dp[0][0] = matrix[0][0];
//计算第一列的值
for(int i = 1; i < row; i ++)
{
dp[i][0] = dp[i - 1][0] + matrix[i][0];
path[i][0] = 0;
}
//计算第一行的值
for(int j = 1; j < col; j++)
{
dp[0][j] = dp[0][j- 1] + matrix[0][j];
path[0][j] = 1;
}
//计算其它的值
for(int i = 1; i < row; i++)
{
for(int j = 1; j < col; j++)
{
int direction = dp[i][j-1] < dp[i-1][j] ? 1 : 0;
dp[i][j] = (direction ? dp[i][j-1] : dp[i-1][j]) + matrix[i][j];
path[i][j] = direction;
}
}//for
return dp[row - 1][col - 1];
}
——dp视差空间代码
// (1) set last entry sink in matrix (last value)
// (2-3) Initializ Edges
// (2) initialize travelpath for last col (only south direction)
// (3) initialize travelpath for last row (only east direction)
// (4) calculate paths till last sink (last entry) till xLast - 1, yLast - 1
// (-) save all (chosen) directions along the way
void DPmat::preCalc(Mat &matrix, Mat &sum, Mat &dirs) {
float occlusion_south = 1.0f;
float occlusion_east = 1.0f;
sum = Mat::zeros(matrix.rows, matrix.cols, matrix.type()); // not initialized with zero, should not be a problem,
dirs = Mat::zeros(matrix.rows, matrix.cols, CV_16U); // because traversion is pre initialized with borders
// dirs = (1, south), (2, south-east), (3, east)
int rowLast = matrix.rows - 1; // last index inclusive
int colLast = matrix.cols - 1; // last index inclusive
// (1) initialize sink (last Entry/ terminal point/ matrix exit value)
sum.at<float>(rowLast, colLast) = matrix.at<float>(rowLast, colLast);
// (2-3) Initialize Edges
// (2) calculate all last row entries down to exit value | only downward directions (so upward pre calculation)
for(int y = rowLast - 1; y >= 0; --y) {
// sum[y,x] = M[y,x] * occlusion_south + sum[y+1,x]
sum.at<float>(y, colLast) = matrix.at<float>(y, colLast) * occlusion_south + sum.at<float>(y + 1, colLast); // add current value + successor min(value)
dirs.at<ushort>(y, colLast) = 1; // south
}
// (3) initialize last
for(int x = colLast - 1; x >= 0; --x) {
// sum[y,x] = M[y,x] * occlusion_east + sum[y+1,x]
sum.at<float>(rowLast, x) = matrix.at<float>(rowLast, x) * occlusion_east + sum.at<float>(rowLast, x + 1); // add current value + successor min(value)
dirs.at<ushort>(rowLast, x) = 3; // east
}
// (4) Main calculation (3 way [south(s), east(e), south-east(se)])
for(int y = rowLast - 1; y >= 0; --y) {
float* sum_ptr = sum.ptr<float>(y);
float* sum_south_ptr = sum.ptr<float>(y+1);
float* mat_ptr = matrix.ptr<float>(y);
ushort* dirs_ptr = dirs.ptr<ushort>(y);
for(int x = colLast - 1; x >= 0; --x) {
// dirs
//float s = sum.at(y + 1, x);
//float se = sum.at(y + 1, x + 1);
//float e = sum.at(y, x + 1);
float s = sum_south_ptr[x] * occlusion_south; // (y+1,x) occlusion dir
float se = sum_south_ptr[x + 1]; // (y+1,x+1)
float e = sum_ptr[x + 1] * occlusion_east; // (y, x+1) occlusion dir
// lowest cost till current point
float p = min(s, min(se, e));
//sum.at(y, x) = p + matrix.at(y, x); // sum till current (cost + lowest path)
sum_ptr[x] = p + mat_ptr[x]; // sum[y,x] = p + mat[y, x]
// selection for traversion direction
//if(p == s) dirs.at(y, x) = 1; // occlusion
//if(p == se) dirs.at(y, x) = 2; // math
//if(p == e) dirs.at(y, x) = 3; // occlusion
if(p == s) dirs_ptr[x] = 1; // occlusion
if(p == se) dirs_ptr[x] = 2; // math
if(p == e) dirs_ptr[x] = 3; // occlusion
}
}
}
void DPmat::disparityFromDirs(Mat &sum, Mat &dirs, Mat &disp, int line, int offset) {
assert(dirs.type() == CV_16U);
// wir bekommen jetzt einen index x, y
int rowLast = dirs.rows - 1;
int colLast = dirs.cols - 1;
int lastval = -1;
int x1 = 0;
int x2 = 0;
float minVal = numeric_limits<float>::max();
int minIndex = 0;
// seek top entry
for(x2 = 0; x2 < sum.cols; ++x2) {
float val = sum.at<float>(x1, x2);
if(val > minVal) {
minIndex = x2;
minVal = val;
}
}
x2 = minIndex;
// safe x1, x2 as disparity match
ushort disparity = abs(x2 - x1);
ushort* disp_ptr = disp.ptr<ushort>(line);
disp_ptr[x1 + offset] = disparity;
while(x1 < rowLast && x2 < colLast) {
ushort d = dirs.at<ushort>(x1, x2);
if(d == 1) { // 1 = down, skipping left index, left got occloded (occlusion from right)
x1++;
if(lastval >= 0) disp_ptr[x1 + offset] = lastval; // dips[line, x1 + offset] = lastval
//disp_ptr[x1 + offset] = 0;
}
if(d == 2) { // match
// next entry will be match
x1++;
x2++;
disparity = abs(x2 - x1);
disp_ptr[x1 + offset] = disparity;
lastval = disparity;
}
if(d == 3) { // 2 = right, skipping right index, occlusion don't care..
x2++;
if(lastval >= 0) disp_ptr[x1 + offset] = lastval; // dips[line, x1 + offset] = lastval
//disp_ptr[x1 + offset]= 0;
}
}
}
原图像:


视差图像:

结论:
这种只考虑了左右相邻像素的视差约束,而忽略了上下领域像素之间的视差约束,这种方法得到的解因此也成为扫描线最优解,不能称为严格意义上的最优解,视图像也出现了明显的横向条纹瑕疵,而且其计算时间也较慢。
(3)视差计算及优化——以SGM算法为例
视差计算
在SGM算法中,视差计算采用赢家通吃(WTA)算法,每个像素选择最小聚合代价值所对应的视差值作为最终视差,视差计算的结果是和左图相同尺寸的视差图,存储每个像素的视差值,在图像内外参数已知的情况下,视差图可以转换为深度图,表示每个像素在空间中的位置。
视差优化
视差优化的目的是为了对通过视差计算得到的视差图进行进一步的处理优化,提出错误视差,提高视差精度,使视差值更可靠,更精确。
剔除错误匹配
错误匹配的直观反应是聚合后某些像素在真实视差位置的代价值并非最小值,有很多因素能够造成这一现象的产生,如噪声,遮挡,弱纹理,重复纹理,算法的局限性等。目前最常用的剔除误匹配的方法为左右一致性法,它基于视差的唯一性约束,即每个像素最多只存在一个正确视差。具体步骤是将左右图像互换位置,再做一次立体匹配,得到另一张视差图。一i那位视差图中每个值所反映的是两个像素之间的对应府岸西,所以根据视差的唯一性约束,通过左图像的视差图,找到每个像素在右乳香的同名点像素及该像素所对应的视差值,这两个视差值之间的差值若小于一定阈值()一般为一个像素),则满足唯一性约束被保留,反之则不满足唯一性约束而被剔除。

除一致性检查之外,剔除小连通区(Remove Peaks),唯一性检测(Uniqueness Check)也是常用的剔除错误视差的方法,可以结合使用。
剔除小连连通区是指剔除视差图中连通的极小块区域,同一个连通区内的视差与邻域视差小于设定阈值(一般为1).
唯一性检测是指对每个像素计算最小代价和次最小代价的值,若两者相对差小于一定阈值,则被剔除。
if ((SecMin-Min)/Min < T) {
disparity = invalid;
}
提高视差精度
提高视差精度采用子像素优化技术,因为视差计算得到的视差图是正像素精度,在很多应用中无法满足精度要求,SGM采用二次曲线内插的方法获得子像素精度,对最优视差的代价值以及前后两个视差的代价值进行二次曲线拟合,曲线的极值点所对应的视差值即为新的子像素视差值。

抑制噪声
为了抑制噪声,小窗口(通常为3*3)的中值滤波是常用的算法。双边滤波也比较常用,能够较好的保持边缘精度,雄安率较中值滤波低。
(4)视差优化


子像素拟合


代码实现(只贴子像素部分)
// 最优视差best_disparity前一个视差的代价值cost_1,后一个视差的代价值cost_2
const sint32 idx_1 = best_disparity - 1 - min_disparity;
const sint32 idx_2 = best_disparity + 1 - min_disparity;
const uint16 cost_1 = cost_local[idx_1];
const uint16 cost_2 = cost_local[idx_2];
// 解一元二次曲线极值
const uint16 denom = std::max(1, cost_1 + cost_2 - 2 * min_cost);
disparity[i * width + j] = best_disparity + (cost_1 - cost_2) / (denom * 2.0f);
嗯,确实很简单!子像素拟合代码位于视差计算函数体内,即在计算最优视差的同时完成子像素拟合。
一致性检查

懒了,码上实战,李迎松:https://blog.csdn.net/rs_lys/article/details/105715526