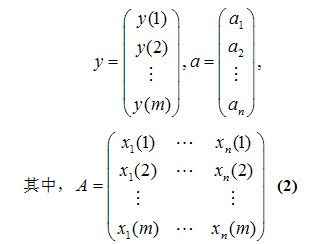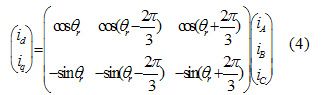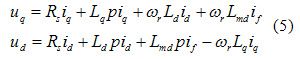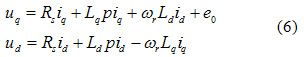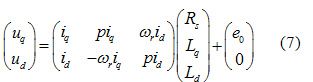matlab最小二乘法参数辨识,基于最小二乘法的永磁同步电机在线参数辨识的仿真...

摘  要：较高性能的永磁同步电机矢量控制系统需要实时更新电机参数，文章中采用一种在线辨识永磁同步电机参数的方法。这种基于最小二乘法参数辨识方法是在转子同步旋转坐标系下进行的，通过MATLAB/SIMULINK对基于最小二乘法的永磁同步电机参数辨识进行了仿真，仿真结果表明这种电机参数辨识方法能够实时、准确地更新电机控制参数。

关键词：永磁同步电机;参数辨识;最小二乘法

Simulation of PMSM based on least squares on-line parameter identification

WANG Hong-shan , ZHANG Xing，XIE Zhen , YANG Shu-ying

Abstract：This paper presents a bbbbbb to determine the parameters of PMSM on line which are necessary to implement the vector control strategy. The presented identification technique, based least-squares, reveals itself suitable to be applied to PMSM. The estimation is based on a standard model of PMSM, expressed in rotor coordinates. The bbbbbb is suitable for online operation to continuously update the parameter values. The developed algorithm is simulated in MATLAB/SIMULINK. Simulation results are presented, and accurate parameters for PMSM is provided.

KEY WORDS：PMSM; Parameter Identification; Least-Squares

0 引言

电机参数辨识方面的文献数量颇多，研究成果丰富。参数辨识技术的研究始于70年代末、80年代初。直至今日，这个领域仍有新的研究成果出现、参数辨识的方法众多，方法与方法之间各有不同。但总的说来，现有的辨识方法可以归纳成5种类型，分别是：信号注入法、直接估算法、补偿坐标系法、最小二乘法、模型参考自适应方法。

信号注入法通过向电机注入测试信号或者已知特性的谐波，并利用频谱特性来辨识电机参数，然而谐波或者测试信号的注入会对控制系统产生不利的影响;扩展的卡尔曼滤波和模型参考自适应控制策略，即使当出现系统和测量噪声时，仍能对电机参数进行准确估计，然而该方案实现起来比较困难。最小二乘理论是高斯在解决天体运动轨道时提出的。最小二乘辨识法是最重要的系统辨识方法之一，也是参数模型的主要辨识方法，得到了广泛的应用。本文在分析永磁同步电机的同步旋转坐标系下方程的基础上运用最小二乘法，通过matlab/simulink仿真环境对永磁同步电机的参数进行辨识，结果表明：这种参数辨识方法能够为准确地辨识出永磁同步电机的参数。

1 基于最小二乘法的永磁同步电机参数辨识

1.1 电机参数辨识的必要性

在交流调速系统中，矢量控制技术能使交流电动机获得与他励直流电动机一样的控制特性，采用矢量控制技术的交流调速系统的性能达到直流调速系统的水平，无速度传感器的矢量控制是在常规带速度传感器的矢量控制基础上发展起来的，在无速度传感器的矢量控制中必须用到电机参数。工程上不能预知现场所用电机的参数，也不可能采用常规的空载试验和堵转试验去测量电机参数，并且随着电机的老化和周围环境的变化，电机实际参数与所给参数之间存在较大的差别，所以作为通用变频器必须具有电机参数的自测定功能。电机投入正常运行之前的参数辨识方法，特别是不需要增加任何附加电路而仅靠电机调速系统本身实现参数辨识方法已成为现代交流电机参数辨识的新特点。从控制的角度来讲, 解决受控对象参数不准的方法之一就是对受控对象的参数进行在线辨识,并不断更新其参数值, 使控制器设定值与实际值相适应。

1.2 最小二乘法的基本原理

最小二乘法最初是由解超定方程，求最优解提出的。设y为一组自变量

的函数，

。若进行m次观测，则：

但m=n时，只要A-1存在，即可求出待定参数：a=(a1,a2...,an)，上式有唯一解：a=A-1y

当m>n时，称为超定方程组，通常不能选定一组参数以满足所有的m个方程，因而需要用估计方法估算最佳值。可以采用最小二乘法进行估计：

1.3 基于最小二乘法的永磁同步电机参数辨识

在基于最小二乘法的电机参数辨识中关键在于如何得到以待辨识参数为未知量的线性方程。下面说明如何在转子同步旋转坐标系下获得以待辨识参数为未知量线性方程的电机模型。

首先用固定于转子的同步旋转坐标dq轴系来分析永磁同步电机的数学模型。取转子永磁体基波励磁磁场轴线(磁极轴线)为d轴，d轴与A相绕组的夹角θr，而q轴(交轴)逆时针方向超前d轴90度电角度，xy坐标系为固定在定子上的旋转坐标系，定子磁链的方向为x轴的正方向，dq轴随同转子以电角速度ωr一起旋转。dq轴上的分量可以由定子三相绕组经三相坐标系或矢量变换得到，即进行三相轴系到两相旋转轴系dq的变换。

以电流的旋转变换为例分析如何得到转子同步旋转坐标系下的电机模型。

式中， θr为转子位置;

为定子的d轴和q轴电流; 

为A轴、B轴和C轴的电流。

通过式(4)的坐标变换可以得到在转子同步旋转坐标系下电机的模型方程：

式中： Rs为定子电阻; Ld为d轴电感; Lq为q轴电感; Lmd为励磁电感; if为等效励磁电流。

在电机中，若不计温度变化对永磁体的供磁的影响，可认为永磁体的基波磁场

是恒定的，即if是个常量。

，实际上是d轴永磁体励磁磁场在q轴线圈中产生的运动电动势，也就是空载电动势e0。式(5)可以化简为：

式(6)写成矩阵形式：

由式(7)可以明显地看出，经过了坐标变换得到了以定子电阻Rs、q轴电感La和d轴电感Ld为未知量的线性方程，可以运用最小二乘法对电机参数进行辨识。

2 基于最小二乘法永磁同步电机参数辨识的仿真模型

在Matlab7.0的Simulink环境下，在分析永磁同步电机数学模型的基础上，建立了永磁同步电机参数辨识系统的仿真模型如图1所示。

图1 基于最小二乘法参数辨识的系统原理框图

系统采用控制方案：根据模块化建模的思想，将控制系统分割为各个功能独立的子模块，其中主要包括：永磁同步电机本体模块、电机运行状态测量模块和最小二乘法参数辨识模块。

通过这些功能模块的有机整合，就可在Matlab/Simulink中搭建出永磁同步电机参数辨识系统的仿真模型，并实现电机参数辨识算法。

其中，最小二乘法参数辨识模块由于需要大量的矩阵运算，采用了M语言进行编写后作为一个模块嵌入Simulink环境中，充分利用Simulink提供模块化环境和M语言的灵活性，做到两者有效结合。

3 仿真结果

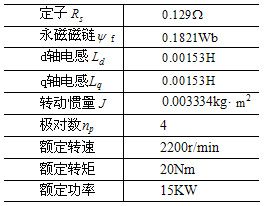
针对上述建立的仿真模型进行了永磁同步电机系统的仿真测试。永磁同步电机参数见表1：

表1 仿真参数

仿真的过程中，在永磁同步电机的转子轴上加-30Nm/s递增的转矩，使永磁同步运行在发电模式的同时，电机处于不停地加速状态，这样做的目的是使得电机的状态方程满足式(7)。仿真的最大步长为 ，采用M语言编写的参数辨识模块于0.53s启动，每隔0.01s进行一次参数辨识。从而每隔0.01s利用新辨识出的电机参数在之前辨识出的电机参数的基础上进行更新，以获得准确的实时电机参数。

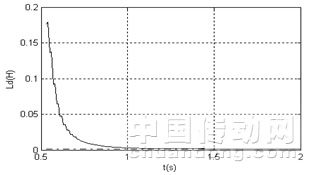
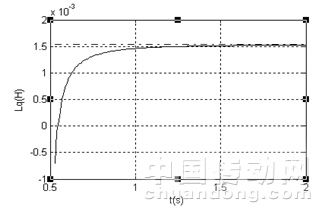
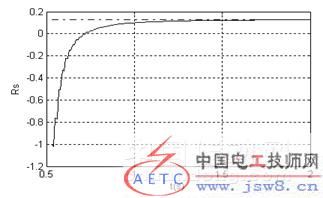
图2是在电机待辨识参数初始值都为0的情况下，对永磁同步电机控制过程中参数辨识的仿真结果：虚线分别表示电机的实际参数值，实线表示参数辨识的结果。从图2的a、b和c图都可以看出从0.53s算法开始运行，永磁电机的d轴和q轴电感包括定子电阻从初始值0开始单调地向电机相应的实际参数进行收敛，并无限地逼近相应电机参数的实际值。

仿真结果表明基于最小二乘法的参数辨识算法能够在线实时准确辨识出电机参数，具有较好的收敛性和辨识精度。

(a)d轴电感

(b)q轴电感

(c) 定子电阻

图2 电机参数辨识结果

4 结 论

为了提高对永磁同步电机的控制性能，本文在永磁同步电机的转子同步旋转坐标系下，采用最小二乘法对电机参数进行辨识，在Matlab/Simulink中搭建出永磁同步电机参数辨识系统的仿真模型。仿真结果表明基于最小二乘法的参数辨识算法能够在线实时准确辨识出电机参数，具有较好的收敛性和辨识精度。