07【其他类】模型——相关性分析

07【其他类】模型——相关性分析

目录

一、引述

二、Person相关系数

2.1 总体和样本

2.1.1 总体person相关系数

2.1.2 样本person相关系数 

2.2  线性相关问题

2.2.1 相关系数不为0不等于线性相关

2.2.2 对于本例各变量之间的散点图

2.3 正态分布检验

2.3.1 JB检验

2.3.2 夏皮洛‐威尔克检验

2.3.3 Q_Q图 

2.4 求相关系数并假设检验 

2.4.1 假设检验的前提条件

2.4.2 假设检验的步骤

三、斯皮尔曼相关系数

3.1 斯皮尔曼相关系数的定义

3.1.1 第一种定义

3.1.2 第二种定义

3.2 假设检验

四、Person与斯皮尔曼相关系数的比较

五、代码

六、总结

---

一、引述

皮尔逊 pearson相关系数和斯皮尔曼spearman等级相关系数。 它们可用来衡量两个变量之间的相关性的大小，根据 数据满足的不同条件，我们要选择不同的相关系数进行计算和分析。

引例：现有某中学八年级所有女学生的体测样本数据，请见下表，试计算各变量之 间的皮尔逊相关系数。

表1-1 某中学八年级所有女学生的体测样本数据

二、Person相关系数

2.1 总体和样本

1. 总体——所要考察对象的全部个体叫做总体。 我们总是希望得到总体数据的一些特征（例如均值方差等）。

2. 样本——从总体中所抽取的一部分个体叫做总体的一个样本。

*由于总体数据过于庞大且难以计算，所以我们通过计算这些抽取的样本的统计量来估计总体的统计量： 例如使用样本均值、样本标准差来估计总体的均值（平均水平）和总体的标准差（偏离程度）。

2.1.1 总体person相关系数

2.1.2 样本person相关系数 

 疑问：计算总体Person系数的分母是n,为什么在计算样本Person相关系数时用的是n-1？

2.2  线性相关问题

相关系数只是用来衡量两个变量线性相关程度的指标；也就是说，你必须先确认这两个变量是线性相关的，然后这个相关系数才能告诉你他俩相关程度如何。通过绘制散点图可以很容易地判定两个数据对象x和y之间的相关性。

2.2.1 相关系数不为0不等于线性相关

图2-1 Person相关系数=0.816的四种散点图

图2-2 冰激凌与温度之间关系的散点图

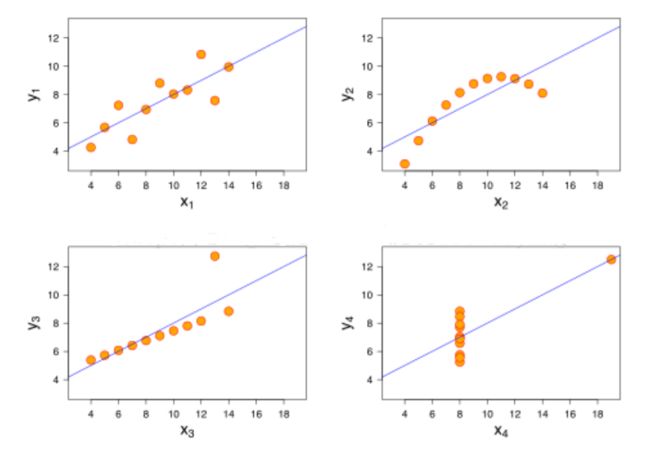
1. 非线性相关也会导致线性相关系数很大，例如图2-1中的右上角。

2. 离群点对相关系数的影响很大，例如图2-1中的左下角，去掉离群点后，相关系数为0.98。

3. 如果两个变量的相关系数很大也不能说明两者相关，例如图2-1中的右下角，可能是受到 了异常值的影响。

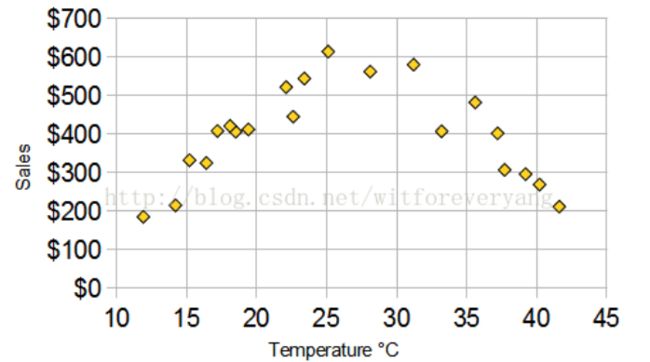
4. 相关系数计算结果为0，只能说不是线性相关，但说不定会有更复杂的相关 关系（非线性相关），例如图5

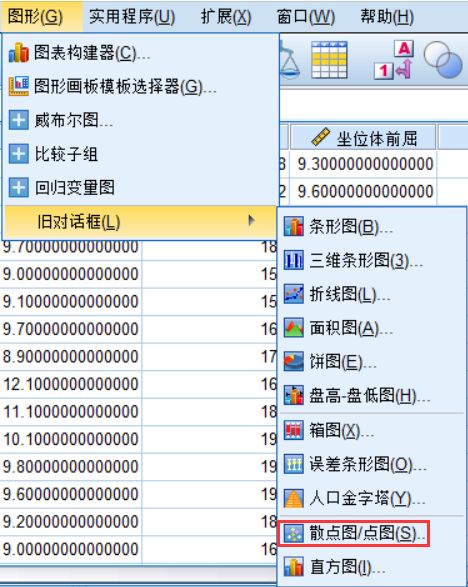
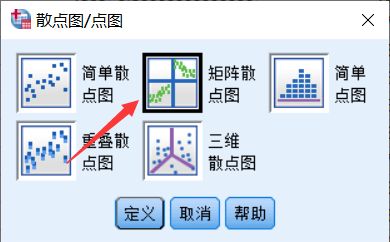
2.2.2 对于本例各变量之间的散点图

图2-3 各变量之间的矩阵散点图

由该矩阵散点图可以看出大部分数据并没有线性相关性，所以就算出来的Person相关系数是没有意义的，并不能表示出两变量之间的相关强度。为了下面过程的进行，这里我们假设各变量之间是线性相关的。

根据散点图，什么样的才是线性相关，什么样的不是线性相关？

如果部分数据线性相关，部分数据线性不相关呢？可以用Person相关系数吗？

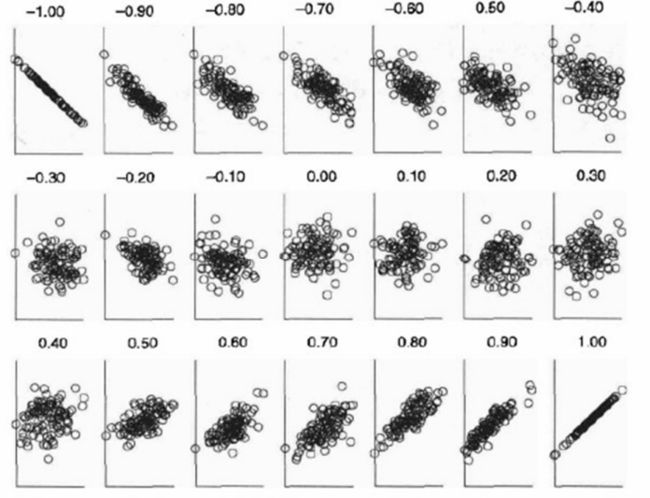
相关系数从-1到1 的散点图如下，可做参考，

图2-4 相关度从-1到1的散点图

2.3 正态分布检验

实验数据通常假设是成对的来自于正态分布的总体。因为我们在求皮尔逊相关性系数以后，通常还会用t检验之类的方法来进行皮尔逊相关性系数检验，而t检验是基于数据呈正态分布的假设的，因此我们需要检验数据是否呈正态分布。

2.3.1 JB检验

偏度和峰度： 

JB检验的步骤： 

• 第一步： 
• 第二步：   
• 第三步：

注意：JB检验适用于大样本n>30,在matlab中有相应的函数jbtest可供调用。

2.3.2 夏皮洛‐威尔克检验

夏皮洛‐威尔克检验步骤：

• 第一步：
• 第二步：  
• 第三步： 

注意：夏皮洛‐威尔克检验适用于小样本3<=n<=50,但在matlab中没有相应的函数可供调用，可用spss软件进行检验（分析->描述性统计->探索->...）。 

2.3.3 Q_Q图 

在统计学中，Q‐Q图（Q代表分位数Quantile）是一种通过比较两个概 率分布的分位数对这两个概率分布进行比较的概率图方法。首先选定分位数的对应概率区间集合，在此概率区间上，点(x,y)对应 于第一个分布的一个分位数x和第二个分布在和x相同概率区间上相同的分位数。

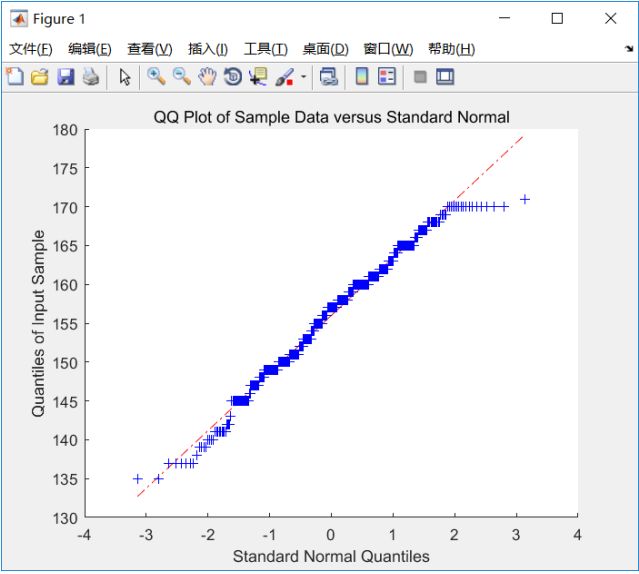
这里，我们选择正态分布和要检验的随机变量，并对其做出QQ图， 可想而知，如果要检验的随机变量是正态分布，那么QQ图就是一条直线。

qqplot(Test(:,1)画图如下，

图2-5 Q_Q图

 注意：要利用Q‐Q图鉴别样本数据是否近似于正态分布,只需看Q‐Q图上的点是否近似地在一条直线附近。（要求数据量非常大）

2.4 求相关系数并假设检验 

为什么进行假设检验？

因为我们计算的相关系数是根据样本来对整体进行估计的，由于估计中抽样误差的存在，所以估计以后还需要进行有关的假设检验。

2.4.1 假设检验的前提条件

1. 实验数据通常假设是成对的来自于正态分布的总体。因为我们在求皮尔 逊相关性系数以后，通常还会用t检验之类的方法来进行皮尔逊相关性系数检验， 而t检验是基于数据呈正态分布的假设的。（相关检验方法在2.3有介绍）

2. 实验数据之间的差距不能太大。皮尔逊相关性系数受异常值的影响比较 大。

3. 每组样本之间是独立抽样的。构造t统计量时需要用到

2.4.2 假设检验的步骤

• 第一步：                
• 第二步：           
• 第三步：         
• 第四步：

  

• 第五步：                      

注明：

1. 置信水平β：即相信原假设成立的概率。
2. 显著性水平α：即有多大可能拒绝原假设。其中β=1-α。
3. 双侧检验和单侧检验
4. p值判别法：上面的p值即[1-（3.05505除对应的概率值）]*2，如果是单侧检验就不用乘以2。之后与显著性水平α作比较，若小于α就拒绝原假设，反之接受原假设。

三、斯皮尔曼相关系数

3.1 斯皮尔曼相关系数的定义

3.1.1 第一种定义

 注明：如果有的数值相同，则将它们所在的位置取算术平均。

3.1.2 第二种定义

斯皮尔曼相关系数第二种定义为：斯皮尔曼关系数就是等级之间的皮尔逊相关系数

matlab中的代码如下，

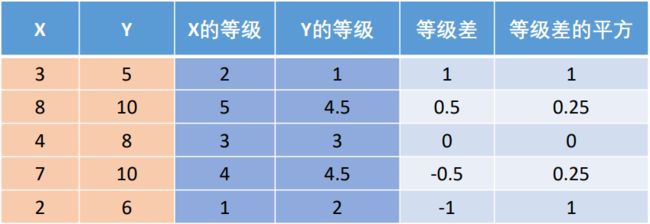
RX = [2 5 3 4 1]；

RY = [1 4.5 3 4.5 2]；

R = corrcoef(RX,RY); %计算RX和RY的Person相关系数

或

X = [3 8 4 7 2]' % 一定要是列向量哦，一撇'表示求转置

Y = [5 10 9 10 6]'

coeff = corr(X , Y , 'type' , 'Spearman');

3.2 假设检验

四、Person与斯皮尔曼相关系数的比较

1. 连续数据，正态分布，线性关系，用pearson相关系数是最恰当，当然用 spearman相关系数也可以， 就是效率没有pearson相关系数高。

2. 上述任一条件不满足，就用spearman相关系数，不能用pearson相关系数。

3. 两个定序数据之间也用spearman相关系数，不能用pearson相关系数。

（定序数据是指仅仅反映观测对象等级、顺序关系的数据，是由定序尺度计量形成的，表现为类别，可以进行排序，属于品质数据。）

4. 斯皮尔曼相关系数的适用条件比皮尔逊相关系数要广，只要数据满足单调关系（例如线性函数、指数函数、对数函数等）就能够使用。

五、代码

//线性相关的检验（SPSS软件）

• 第一步：导入数据                                              

  

                
• 第二步：选择“散点图”                                                                  

  

• 第三步：选择“矩阵散点图”                                                                                                      

  

•  第四步：得到矩阵散点图                                                                                      

  

//FileName：G_normTest.m

%% 正态分布检验——jb检验
clear;clc;
load 'physical fitness test.mat';
[n1,n2]=size(Test);%得到数据的行列大小
H=zeros(1,6);%初始化数据
P=zeros(1,6);
for i=1:n2%对每一列数据进行jb检验
    [h,p]=jbtest(Test(:,i),0.05);
    H(i)=h;
    P(i)=p;
end
disp(H);
disp(P);

%%注明：
% 1. MATLAB中进行JB检验的语法：[h,p] = jbtest(x,alpha)
% 当输出h等于1时，表示拒绝原假设；h等于0则代表不能拒绝原假设。
% alpha就是显著性水平，一般取0.05，此时置信水平为1‐0.05=0.95
% x就是我们要检验的随机变量，注意这里的x只能是向量

//FileName：G_Person.m

%% Person相关系数
% 当各变量之间呈线性关系且各变量的数据成正态分布时使用Person相关系数
clear,clc;
load 'physical fitness test.mat';

%计算各列之间的Person相关系数以及p值
[R,P]=corrcoef(Test);%Test矩阵各列之间的Person相关系数
sign=P<0.05;%找到P值小于0.05的，即拒绝原假设的部分
disp(R);
disp(P);
disp(sign);

//FileName：G_Spearman.m

%% 斯皮尔曼相关系数
%当各变量不是线性相关或数据不连续、不成正态分布时可用斯皮尔曼相关系数
clear,clc;
load 'physical fitness test.mat';
[R,P]=corr(Test,'type','Spearman');%求斯皮尔曼相关系数以及p值
disp('R=');disp(R);
disp('P=');disp(P);
disp(P<0.05);

//模拟假设检验原理（这部分为拓展） 

%% 假设检验部分

% Person相关系数=0.5,构造的统计量t=rs*sqrt((n-2)/(1-rs^2)),自由度为n-2(28)
% 根据置信水平95%求接受域
clear,clc;
x=-4:0.1:4;
y=tpdf(x,28);%求t分布,自由度为28
%figure(1);
plot(x,y,"b-")
grid on

hold on
x_1=tinv(0.975,28);%求P(X<=x)=0.975对应的x值
y_1=tpdf(x_1,28);
plot([x_1,x_1],[0,y_1],"r-");
plot([-x_1,-x_1],[0,y_1],"r-");

% 求p值
t = 0.5*sqrt(28/(1-0.5^2));
p=(1-tcdf(t,28))*2; %tcd函数为tinv函数的反函数
disp(p<0.05);

%斯皮尔曼相关系数=0.5,构造统计量z=rs*sqrt(n-1)
x1=-4:0.1:4;
y1=normpdf(x1,0,1);
figure(2);
plot(x1,y1,'b-');
grid on

hold on
x1_1=norminv(0.975);
y1_1=normpdf(x1_1);
plot([-x1_1,-x1_1],[0,y1_1],'r-');
plot([x1_1,x1_1],[0,y1_1],'r-');

%计算p值
z=0.5*sqrt(30-1);
p1=(1-normcdf(z))*2;
disp(p1<0.05);

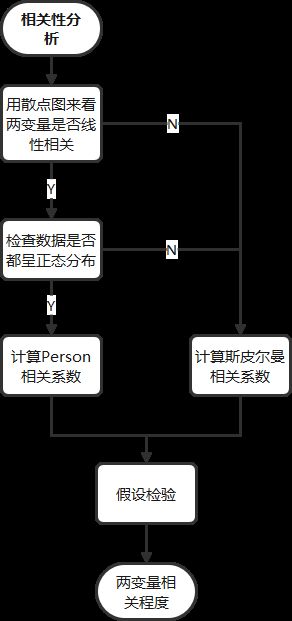
六、总结

本章节知识点总结如下图，

图5-1 本章节知识点流程图

疑问：

1. 相关性分析在什么时候用？
2. 相关系数的假设检验为什么是要显著于0？ 
3. t分布和t检验是什么？统计量如何构造的？
4. 什么样的散点图才是线性的？

结束语：本文部分内容来自于B站“数学建模学习交流”以及疯学网数学建模系列教程