sift算法_基于单目视觉的三维重建算法综述
三维计算机视觉在计算机视觉是偏基础的方向,随着2010年阿凡达在全球热映以来,三维计算机视觉的应用从传统工业领域逐渐走向生活、娱乐、服务等,比如AR/VR,SLAM,自动驾驶等都离不开三维视觉的技术。
三维重建包含三个方面,基于SFM的运动恢复结构,基于Deep learning的深度估计和结构重建,以及基于RGB-D深度摄像头的三维重建。
图 1基于图像的三维重建算法SfM(Structure From Motion),主要基于多视觉几何原理,用于从运动中实现3D重建,也就是从无时间序列的2D图像中推算三维信息,是计算机视觉学科的重要分支。广泛应用于AR/VR,自动驾驶等领域。虽然SFM主要基于多视觉几何原理,随着CNN的在二维图像的积累,很多基于CNN的2D深度估计取得一定效果,用CNN探索三维重建也是不断深入的课题。
深度学习方法呈现上升趋势,但是传统基于多视几何方法热情不减,实际应用以多视几何为主,深度学习的方法离实用还有一定的距离。
本综述主要介绍基于单目monocular的三维重建方法,主要分为基于SfM三维重建和基于Deep learning的三维重建方法,另外由于多视觉几何涉及大量的矩阵、线性代数和李群等数学概念,本综述不做进一步研究,详细可参考经典多视觉几何MVG。
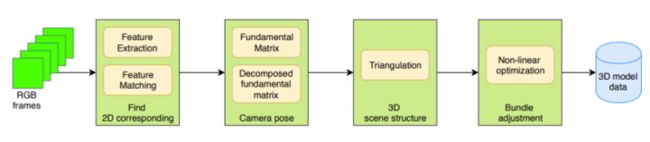
图 2基于图像的三维重建基本流程1、SfM 与三维重建
从二维图像中恢复三维场景结构是计算机视觉的基本任务,广泛应用于3D导航、3D打印、虚拟游戏等。
Structure from Motion(SfM)是一个估计相机参数及三维点位置的问题。一个基本的SfM pipeline可以描述为:对每张2维图片检测特征点(feature point),对每对图片中的特征点进行匹配,只保留满足几何约束的匹配,最后执行一个迭代式的、鲁棒的SfM方法来恢复摄像机的内参(intrinsic parameter)和外参(extrinsic parameter)。并由三角化得到三维点坐标,然后使用Bundle Adjustment进行优化。
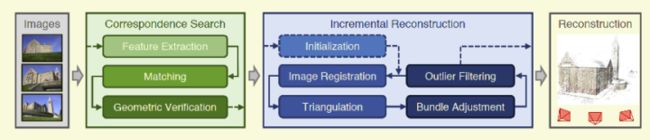
图 3 SfM典型框架图根据SfM过程中图像添加顺序的拓扑结构(图 4),SfM方法可以分为增量式(incremental/sequential SfM),全局式(global SfM),混合式(hybrid SfM),层次式(hierarchica SfM)。另外有基于语义的SfM(Semantic SfM)和基于Deep learning的SfM。
图 4增量式、全局式、混合式和层次式SFM拓扑结构区别1.1 增量式 SfM
以[1]的方法位置,增量式SfM首先使用SIFT特征检测器提取特征点并计算特征点对应的描述子(descriptor),然后使用ANN(approximate nearest neighbor)方法进行匹配,低于某个匹配数阈值([1]中的阈值为20)的匹配对将会被移除。对于保留下来的匹配对,使用RANSAC(RANdom Sample Consensus)和八点法来估计基本矩阵(fundamental matrix),在估计基本矩阵时被判定为外点(outlier)的匹配被看作是错误的匹配而被移除。对于满足以上几何约束的匹配对,将被合并为tracks。然后通过incremental方式的SfM方法来恢复场景结构。首先需要选择一对好的初始匹配对,一对好的初始匹配对应该满足:
(1)足够多的匹配点;
(2)宽基线。之后增量式地增加摄像机,估计摄像机的内外参并由三角化得到三维点坐标,然后使用Bundle Adjustment进行优化。
增量式SfM从无序图像集合计算三维重建的常用方法。在[1]的基础上,增量式SfM可分为如图 3所示几个阶段:图像特征提取、特征匹配、几何约束、重建初始化、图像注册、三角化、outlier过滤、Bundle adjustment等步骤。
图 5 增量式SfM框架图实现增量式SfM框架的包含COLMAP、openMVG、Theia等,如图 6所示典型增量式SfM框架在增量式SfM算法各个阶段的细节对比。
图 6 增量式SfM实现框架对比增量式SfM优势:系统对于特征匹配以及外极几何关系的外点比较鲁棒,重讲场景精度高;标定过程中通过RANSAC不断过滤外点;捆绑调整不断地优化场景结构。
增量式SfM缺点:对初始图像对选择及摄像机的添加顺序敏感;场景漂移,大场景重建时的累计误差。效率不足,反复的捆绑调整需要大量的计算时间。
1.2 全局式SfM
全局式:估计所有摄像机的旋转矩阵和位置并三角化初始场景点。
优势:将误差均匀分布在外极几何图上,没有累计误差。不需要考虑初始图像和图像添加顺序的问题。仅执行一次捆绑调整,重建效率高。
缺点:鲁棒性不足,旋转矩阵求解时L1范数对外点相对鲁棒,而摄像机位置求解时相对平移关系对匹配外点比较敏感。场景完整性,过滤外极几何边,可能丢失部分图像。
1.3 混合式SfM
混合式SfM[5]在一定程度上综合了incremental SfM和global SfM各自的优点。HSfM的整个pipeline可以概括为全局估计摄像机旋转矩阵,增量估计摄像机位置,三角化初始场景点,如图 7所示。
图 7 全局式SfM框架图用全局的方式提出一种基于社区的旋转误差平均法,该方法既考虑了对极几何的精度又考虑了成对几何的精度。基于已经估计的相机的绝对旋转姿态,用一种增量的方式估计相机光心位置。对每个添加的相机,其旋转和内参保持不变,同时使用改进的BA细化光心和场景结构。
层次式SfM同样借鉴incremental SfM和global SfM各自优势,但是基于分段式的incremental SfM和全局式SfM,没有像混合式SfM分成两个阶段进行。
SfM中我们用来做重建的点是由特征匹配提供的,所以SfM获得特征点的方式决定了它不可能直接生成密集点云。而MVS则几乎对照片中的每个像素点都进行匹配,几乎重建每一个像素点的三维坐标,这样得到的点的密集程度可以较接近图像为我们展示出的清晰度。
1.4 三维场景重建实例
初学者容易陷入MVG等大部头经典书籍理解基于多视觉几何的公式,从一个实际例子理解实现更容易建立信心。本节简单介绍利用openMVG和PMVS实现三维场景的点云重建。
openMVG (Open Multiple View Geometry):开源多视角立体几何库,这是一个cv界处理多视角立体几何的著名开源库,信奉“简单,可维护”,提供了一套强大的接口,每个模块都被测试过,尽力提供一致可靠的体验。
openMVG实现以下典型应用:
- 解决多视角立体几何的精准匹配问题;
- 提供一系列SfM需要用到的特征提取和匹配方法;
- 完整的SfM工具链(校正,参估,重建,表面处理等);
- openMVG尽力提供可读性性强的代码,方便开发者二次开发,核心功能是尽量精简的,所以你可能需要其它库来完善你的系统。
github地址:https://github.com/openMVG/openMVG
使用文档:http://openmvg.readthedocs.io/en/latest/
从git克隆openMVG到本地(支持windows vs2015/linux/mac环境),安装必要的依赖库(缺少依赖库时cmake或make会报错,也可根据提示安装)。
$ git clone --recursive https://github.com/openMVG/openMVG.git
$ mkdir openMVG_Build
$ cd openMVG_Build
$ cmake -DCMAKE_BUILD_TYPE=RELEASE -DOpenMVG_BUILD_TESTS=ON -DOpenMVG_BUILD_EXAMPLES=ON . ../openMVG/src/
$ make
$ make testCMVS-PMVS(a modified version):将运动结构(SfM)软件的输出作为输入,然后将输入图像分解成一组可管理大小的图像簇。 MVS软件可以用来独立和并行地处理每个簇,其中来自所有簇的重建不错过任何细节。
Github地址:https://github.com/pmoulon/CMVS-PMVS
CMVS-PMVS编译也比较简单,切换到克隆源码目录,
$ mkdir build && cd build
$ cmake ..
$ make既可完成编译,build/main文件夹中生成cmvs、genOption、pmvs2三个可执行文件。
首先cd到openMVG_Build/software/SfM/文件夹中,在终端运行$ python tutorial_demo.py
它是封装了SfM pipeline的脚本,它先克隆文件夹ImageDataset_SceauxCastle到SfM文件夹中,作为图像输入
再生成一个tutorial_out文件夹保存输出结果
由于openMVG生成的是稀疏的点云,只含有它在图像中提取到的特征点的点云映射,所以需要用PMVS处理图像和位置的关系来得到稠密的点云。
SfM_Data是一个数据容器,储存在sfm_data.bin中,它包括(大概也就是二进制编码的结构):
Views - 图像
Intrinsics – 相机内参数
Poses – 相机外参数
Landmarks – 三维点和它们的二维图像对应点
把SfM_Data转化为适用于PMVS输入格式的文件
$ openMVG_main_openMVG2PMVS -i tutorial_out/reconstruction_global/sfm_data.bin -o tutorial_out/reconstruction_global在reconstruction_global文件夹中会生成PMVS文件夹,包含 models, txt, visualize 三个文件夹,models为空,txt包含11个对应图像的txt文档,每个里面都是一个3x4的矩阵,大概是相机位姿,visualize包含11张图像,不确定是原图像还是校正过的图像。切换到tutorial_out/reconstruction_global目录,
$ pmvs2 ./PMVS/ pmvs_options.txtPMVS/models文件夹中生成一个大小为15.2MB的pmvs_options.txt.ply点云文件,用meshlab打开即可看到重建出来的彩色稠密点云,如所示。
图 8 三维重建效果图2、Deep learning与三维重建
常规的3D shape representation主要有四种: 深度图(depth), 点云(point cloud), 体素(voxel), 网格(mesh)。
2.1 深度估计
假设我们有一张2d图片I,我们需要一个函数F来求取每个像素其相对应的深度 d,这个过程可以写为: d=F(I)。
图 9 单幅无法图像估计深度但是众所周知,F 是非常复杂的函数,因为从单张图像中获取具体的深度相当于从二维图像推测出三维空间,即使人类的双眼也无法获取深度信息,如图 9所示,人类无法判断所谓的巨人手掌上是模型还是摆拍(如果前方巨人换成孙大圣到是有可能,不过已经变成玄幻电影)。所以传统的深度估计在单目深度估计上效果并不好。人们更着重于研究多视觉几何,即从多张图片中得到深度信息。因为两张图片就可以根据视角的变化得到图片之间disparity的变化,从而达到求取深度的目的。
随着2012年CNN在二维图像取得巨大成就,涌现很多基于CNN的depth map:因为depth map本身是一个监督学习,真值可以通过激光/结构光等深度传感器获取,而分辨率和输入图像相同,本质是一个二维图像像素分类的问题难题。但是depth image还不足以解释重构原始input的信息,它只能作为3D scene understanding的一个辅助信息。所以开始研究利用一组二维图来重构3D点云图或voxel以及mesh图。
使用深度学习做深度估计最经典的两篇文章应该属于Eigen组[6][7]的两篇工作:
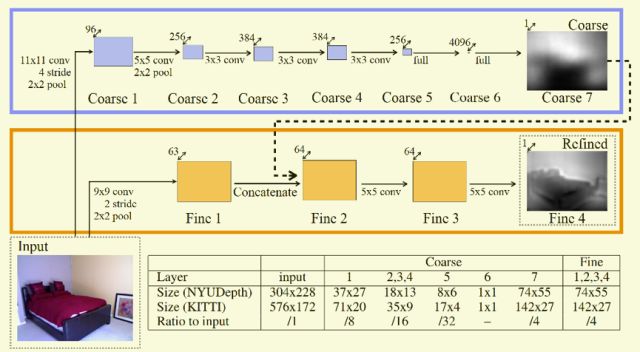
在NIPS2014[6]的文章中, 如所示,作者提出了一个Multi-Scale的深度神经网络用来解决深度预测的问题。Coarse 网络是一个经典的AlexNet(NIPS 212)结构,最后一层从1000个分类器换做了一个coarse的depth map。在Fine网络中,作者先采用大步长的卷积核将图片的大小变小之后的卷积核并没有再去降低特征的大小,而是采用了步长为1,大小为5的卷积核去进行特征提取并结合之前Coarse网络的结果得到最终预测的结果。在训练的时候,此网络先训练Coarse网络然后再固定Coarse网络的训练参数再去训练Fine网络。
在此基础上,FCRN尝试了更深层次的网络带来的好处:使用一个pretrained的ResNet50结构,采用经典的卷积和反卷积架构,效率提升一倍。
图 10 Multi-Scale depth map预测随着深度学习的发展,涌现很多基于视频[9]的depth map预测。
2.2 3D shape预测
但是depth image还不足以解释重构原始input的信息,它只能作为3D scene understanding的一个辅助信息。
基于deep learning的3D点云和mesh重构是较难以计算的,因为深度学习一个物体完整的架构需要大量数据的支持。然后传统的3D模型是由vertices和mesh组成的,因此不一样的data size造成了training的困难。所以后续大家都用voxelization(Voxel)的方法把所有CAD model转成binary voxel模式(有值为1, 空缺为0)这样保证了每个模型都是相同的大小。
[10]采用深度学习从2D图像到其对应的3D voxel模型的映射:首先利用一个标准的CNN结构对原始input image进行编码,然后用Deconv进行解码,最后用3D LSTM的每个单元重构output voxel。3D voxel是三维的,它的resolution成指数增长,所以它的计算相对复杂,目前的工作主要采用32*32*3以下的分辨率以防止过多的占用内存。但是也使得最终重构的3D model分辨率并不高。所以科研道路道阻且长。
mesh和point cloud是不规则的几何数据形式,因此直接使用CNN是不可行的。但是可以考虑将3D mesh data转化成graphs形式,再对3D曲面上的2D参数进行卷积。具体有[11]。
基于point cloud的方法,看Hao Su的CVPR2017论文 PointNet[12]。
基于mesh和point cloud的方法总的来讲数学较多,而且重建细节恢复上效果欠佳。不过可以考虑voxel来提高重构精度。
3、三维视觉发展趋势
趋势1:多视觉几何与Deep learning方法融合
在深度学习一统天下的计算机视觉领域,三维视觉方向主导算法仍然是传统的多视角几何方法,但是深度学习方法也是一种重要而有效的辅助,比如在解决单目初始化纯旋转问题上。
趋势2:多传感器融合
目前基于普通摄像头的视觉传感器仍然是主导,但是工业界对算法的鲁棒性要求比较高,纯视觉方法很难保证在复杂的环境下保持鲁棒的效果。所以,用廉价的激光传感器、IMU(惯性测量单元)等与视觉传感器进行融合,是一种比较靠谱的方法。比如在移动端目前基于摄像头+IMU方法越来越多。
趋势3:算法与硬件的结合
比如深度相机厂商在尽力把一些视觉算法嵌入到相机前端,提升相机的本地处理能力。2018年发表在Robotics & Autonomous Systems 的一篇论文 《Embedding SLAM algorithms: Has it come of age? 》讨论了嵌入式SLAM算法的可能性,并给出了一种在低功耗嵌入式系统上实现SLAM的算法:FastSLAM2.0。
趋势4:算法与具体应用的结合能够更快的推动算法进步
三维视觉算法目前比较好的商业应用主要集中在无人驾驶、无人搬运车(Automatic Guided Vehicle,简称AGV)、AR(教育、影音游戏)、机器人等领域。
4、Discussion
个人观点:
1、尽管SfM在计算机视觉取得显著成果并应用,但是大多数SfM和基于周围环境是静止这一假设,既相机是运动的,但是目标是静止的。当面对移动物体时,整体系统重建效果显著降低。
2、传统SfM基于目标为刚体的假设。
3、个人对3D重建算法不是深入,SfM也许没有vSLAM技术热点,但是多视觉几何和SfM是进入三维世界的大门,基础应用永不过时。
以上仅为个人阅读论文后的理解、总结和思考。观点难免偏差,望读者以怀疑批判态度阅读,欢迎交流指正。
参考文献
[1] Seitz S M, Szeliski R, Snavely N. Photo Tourism:Exploring Photo Collections in 3D[J]. Acm Transactions on Graphics, 2006, 25(3):835-846.
[2] Agarwal S,Snavely N, Simon I, et al. Building Rome in a day[J]. Communications of the Acm, 2011, 54(10):105-112.
[3] Toldo R,Gherardi R, Farenzena M, et al. Hierarchical structure-and-motion recovery from uncalibrated images[J]. Computer Vision & Image Understanding, 2015,140(C):127-143.
[4] Chen Y,Chan A B, Lin Z, et al. Efficient tree-structured SfM by RANSAC generalized Procrustes analysis[J]. Computer Vision & Image Understanding, 2017,157(C):179-189.
[5] H Cui , X Gao,S Shen, Z Hu. HSfM: Hybrid Structure-from-Motion[C]// Computer Vision and Pattern Recognition. IEEE, 2017.
[6] D. Eigen, C. Puhrsch, and R. Fergus. Depth map prediction from a single image using a multi-scale deep network. NIPS,2014.
[7] D. Eigen,R. Fergus.Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture.ICCV2015
[8] Iro Laina , Christian Rupprecht .Deeper Depth Prediction with Fully Convolutional Residual Networks.2016
[9] V.Sudheendra, Susanna Ricco .SfM-Net: Learning of Structure and Motion from Video.arxiv2017
[10] Christopher B. Choy, Danfei Xu, JunYoung Gwak.3D-R2N2: A Unified Approach for Single and Multi-view 3D Object Reconstruction.ECCV2016.
[11] Jonathan Masciy∗ Davide Boscainiy∗ Michael M. Bronstein.Geodesic convolutional neural networks on Riemannian manifolds.AAAI2018.
[12] Charles R. Qi, Hao Su, Kaichun Mo, Leonidas J. Guibas.PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation.CVPR2017.
原发表于SIGAI人工智能讲堂,转载请注明原作者。