神经网络模型原理
神经网络的定义:神经网络模型是由具有适应性的简单单元组成的广泛并行互联的网络。
神经网络最重要的基本单位是神经元模型。M-P神经元是最典型的代表。
M-P神经元(假设连接着其他n个神经元):
输入端:收到n个神经元传递的输入信号,这些信号带着权重![]() 的连接进行传递,
的连接进行传递,
神经元:把接收到的总输入值和神经元的阈值![]() 进行比较,然后通过激活函数处理并产生神经元的输出。
进行比较,然后通过激活函数处理并产生神经元的输出。
激活函数:一个简单的例子是阶跃函数,输出0/1.
感知机和多层网络:
感知机:
感知机由两层神经元组成——输入层和输出层
输入层接受输入并传递给输出层,输出层是一个M-P神经元。我们通过感知机可以容易的实现逻辑或,与,非运算。
通常对于![]() 和
和![]() 可以通过迭代中的学习过程得到。有公式:
可以通过迭代中的学习过程得到。有公式:
![]()
![]()
对于![]() 我们称之为学习率范围在0到1之间,而这些都是建立在将
我们称之为学习率范围在0到1之间,而这些都是建立在将![]() 看做是一个固定输入为-1的节点。
看做是一个固定输入为-1的节点。
优点:感知机可以处理大部分线性可分得问题,几乎是全部。
缺点:简单的非线性问题感知机都无法解决,且学习能力非常有限。
对于非线性问题我们需要考虑使用多层神经元,多层神经元可以是多个感知机构成的也可以是具有隐层的神经元。
隐层神经元:具有激活函数的功能的功能神经元。
神经网络所学习到的东西可以说基本蕴含在了连接权和阈值中。
误差比传播算法:
上面提到多层神经网络,而多层神经网络的学习算法也比上面提到的感知机的学习算法更加复杂。而误差逆传播算法就是其中杰出的代表(BP算法)。
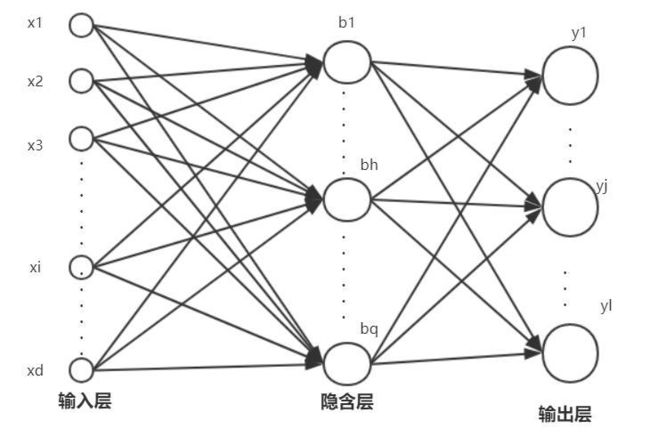
先介绍多层前馈网络结构:
每个神经元和下一层的每一个神经元进行连接,不存在同层相连和跨层连接。
输入层神经元接受外界输出,而隐层神经元和输出层神经元对输入进行功能处理。
基于BP算法的多层前馈神经网络:
假设样本有d个属性描述,输入l维的实值向量。训练集![]()
输出层的第J个神经元的阈值用![]() 表示
表示
隐层的第H个神经元的阈值用![]() 表示
表示
输入层第i个神经元和隐层的第h个神经元之间的连接权重为![]()
隐层第h个神经元和输出层的第j个神经元之间的连接权重为![]()
假设对于输入样例![]() ,假定神经网络的输出为
,假定神经网络的输出为![]()
![]()
BP算法是一个迭代算法,在迭代的每一轮采用感知机学习规则(上面有介绍)对参数进行更新估计。
对于隐层到输出层的连接权重![]() 举例:BP算法基于梯度下降策略
举例:BP算法基于梯度下降策略
对于均方误差![]() ,给定学习率
,给定学习率![]() ,有
,有
对于![]() 可以对其进行分解,注意到
可以对其进行分解,注意到![]() 对
对![]() 的影响并不是直接的,而是先影响到第j个输出层神经元的输入值
的影响并不是直接的,而是先影响到第j个输出层神经元的输入值![]() ,在影响其输出值
,在影响其输出值![]() ,然后影响到
,然后影响到![]() 的,所以
的,所以
对于隐层和输出层神经元我们的激活函数采用Sigmoid函数,此函数有一个性质![]()
![]() 类似的也可以得到其它参数的更新公式
类似的也可以得到其它参数的更新公式
BP算法先将输入示例给予输入层神经元,然后逐层将信号传出知道产生输出层的结果。然后计算误差,在逆向传播给隐层神经元,最后根据隐层神经元的误差来对连接权重和阈值进行调整。
BP算法的目标是最小化训练集D上的累计均方误差。但上面介绍的都是针对单个均方误差的推导而得的(标准BP算法)。如果类似的推导出基于累计误差最小化的更新规则,就得到了累积误差逆传播算法。
标准BP算法:参数更新得非常频繁,对于不同的样例可能产生抵消的现象,因此通常标准BP算法需要更多次数的迭代。
累计BP算法:直接针对累计误差最小化,在读取整个训练集后才对参数进行更新。
神经网络过拟合问题:
早停:将数据分为训练集和验证集,训练集用来计算梯度,更新连接权重和阈值。验证集用来估算误差,若训练集误差降低但验证机误差升高,则停止训练
正则化:在误差目标函数中增加一个用于描述网络复杂度的部分。
全局最小和局部最小:
全局最小:参数空间内所有的点的误差函数值均不小于该点的误差函数值。(只有一个)
局部最小:该点临近的参数空间所有的点的误差函数值均不小于该点的误差函数值。(可有一个或者多个)
基于梯度搜索:
每次迭代中我们先计算误差函数在当前点的梯度,然后根据梯度搜索方向。例如负梯度是函数值下降最快的方法,若误差函数在当前点的函数值为0,则已经达到局部最小。
若只有一个局部最小点那么这个点也就是全局最小点,但是如果同时有多个全局最小点,那么不能保证找到的解是全局最小的。通常通过以下策略试图跳出局部小:
模拟退火
随机梯度下降
遗传算法