传统图像去噪方法（三）之非局部均值去噪（NLM）

前面基于邻域像素的滤波方法，基本上只考虑了有限窗口范围内的像素灰度值信息，没有考虑该窗口范围内像素的统计信息如方差，也没有考虑整个图像的像素分布特性，和噪声的先验知识。

NLM算法使用自然图像中普遍存在的冗余信息来去噪，它利用了整幅图像来去噪，以图像块为单位在图像中寻找相似区域，再对这些区域求平均，能够比较好的去掉图像中存在的高斯噪声。
基本思想是：当前像素的估计值由图像中与它具有相似邻域结构的像素加权平均得到。
TV算法在平滑噪声的同时也把很多图像本身的纹理边缘细节去掉。而（各向异性滤波）AD算法在保持细节信息的同时也保留了很多的噪声。而NL算法则在去除噪声和保持纹理细节方面都取得比较好的效果。
下图是NL-means算法执行过程，大窗口是以目标像素为中心的搜索窗口，两个灰色小窗口分别是以x,y为中心的邻域窗口。其中以y为中心的邻域窗口在搜索窗口中滑动，通过计算两个邻域窗口间的相似程度为y赋以权值 。

（一）opencv自带的NLM算法

1. cv2.fastNIMeansDenoising()使用对象为灰度图像
2. cv2.fastNIMeansDenoisingColored()使用对象为彩色图像
3. cv2.fastNIMeansDenosingMulti()适用于短时间的图像序列（灰度图像）
4. cv2.fastNIMeansDenoisingColoredMulti()适用于短时间的图像序列（彩色图像）

void fastNlMeansDenoising( InputArray src, OutputArray dst, float h = 3, int templateWindowSize = 7, int searchWindowSize = 21);
 # scr 必须为u8
 # h  参数决定滤波器强度。较高的h值可以更好地消除噪声，但也会删除图像的细节 (10 is ok)
 # templateWindowSize  邻域窗口大小
 # searchWindowSize  搜索窗口大小

void fastNIMeansDenoisingColored( InputArray src, OutputArray dst, float h = 3, float hColor = 3, int templateWindowSize = 7, int searchWindowSize = 21);
# hForColorComponents：与h相同，但仅适用于彩色图像。 （通常与h相同）

void fastNlMeansDenoisingMulti( InputArray Of Arrays srcImgs, OutputArray dst,int imgToDenoiseIndex, int temporalWindowSize,  float h = 3, int templateWindowSize = 7, int searchWindowSize = 21);

void fastNlMeansDenoisingColoredMulti( InputArray Of Arrays srcImgs, OutputArray dst, int imgToDenoiseIndex, int temporalWindowSize, float h = 3, float hColor = 3,int templateWindowSize = 7, int searchWindowSize = 21);

非局部均值去噪最优参数选取：

(二）自定义NLM算法

1.PSNR指标

PSNR 和 MSE 就是基于这种简单直接的思路确定的指标，MSE（Mean Squared Error），顾名思义，定义略。PSNR（Peak Signal to Noise Ratio），峰值信噪比，即峰值信号的能量与噪声的平均能量之比，通常表示的时候取 log 变成分贝（dB），由于 MSE 为真实图像与含噪图像之差的能量均值，而两者的差即为噪声，因此 PSNR 即峰值信号能量与 MSE 之比。定义式如下：

第二个等式由于图像像素点数值以量化方式保存，bits 即每个像素点存储所占的位数。因此 MaxValue 即为 2^bits - 1。

def psnr(A,B):
    val=255
    mse=((A.astype(np.float)-B)**2).mean()
    return 10*np.log10((val*val)/mse)

因为灰度图像一般存储为8bit，所以val=255

2.给图像加高斯噪声

给加高斯噪声的意思，就是在原图像矩阵上面加一个符合高斯或者叫正态分布特征的矩阵。
生成随机噪声的三个方法,如果我们的目标矩阵是一个r*c的矩阵，要生成一个均值是mean，标准差sigma的随机噪声矩阵，那么是这样

 sigma*np.random.randn(r,c)+mean, #输入是两个参数，一个mean，一个sigma

 sigma*np.random.standard_normal((r,c)) #输入是一个tuple，里面包含两个元素。  和上面那个是完全一样的。 

 numpy.random.normal(mean,sigma, size=(r,c))  #mean，sigma和大小都作为输入放进函数了。

image读取出来的图像，类型是uin8的（也就是取值范围是0-255），我们计算的随机噪声值，可能是或负或正的小数，直接叠加噪声的图像img_with_noise，其实是有可能是负值，有可能超了255的，而且这个np.ndarray类型是普通的float64了，这个时候用imshow函数来显示，会出现全白全黑的图像bug。
解决方法是在显示前将图像做归一化normalization转成0-255区间的unint类型。
现在看看生成噪声图像的代码：

def double2unit8(I,L,ratio=1.0,sigma=20.0):
    I=I.astype(np.float64)  # 转换成float形式便于计算
    noise=np.random.randn(*I.shape)*sigma  # 生成的时形状与I相同，均值为0，标准差为sigam的随机高斯噪声矩阵
    noisy=I+noise # 噪声图像
    return np.clip(np.round(noisy*ratio),0,255).astype(L.dtype) # 转换回图像的unit8均值，限制在0--255

clip(a, a_min, a_max, out=None):
将数组a中的所有数限定到范围a_min和a_max中，即az中所有比a_min小的数都会强制变为a_min，a中所有比a_max大的数都会强制变为a_max.

np.round(a,b)
第一个参数为待操作数据，第二个为小数点后几位，默认取整

3.生成高斯核

def make_kernel(f):   # 计算得到一个高斯核，用于后续的计算
    kernel=np.zeros((2*f+1,2*f+1))
    for d in range(1,f+1):
        kernel[f-d:f+d+1,f-d:f+d+1] += (1.0/((2*d+1)**2))
    return kernel/kernel.sum()

4.NLM

def NLmeansfilter(I,L,h_=10,templateWindowSize=5,searchWindowSize=11):       
    I=I.astype(np.float64)
    f=int(templateWindowSize/2)
    t=int(searchWindowSize/2)
    height,width=I.shape[:2]  # 利用ndarray的索引得到长宽
    padLength=t+f
    I2=np.pad(I,padLength,'symmetric')   # symmetric——表示对称填充，每侧填充均为padLength  
    kernel=make_kernel(f)
    h=(h_**2)
    I_=I2[padLength-f:padLength+f+height,padLength-f:padLength+f+width]  # 在原图大小的基础上，上下左右均延拓了f大小的图，固定的领域窗口y
 
    average=np.zeros(I.shape)
    sweight=np.zeros(I.shape)
    wmax=np.zeros(I.shape)
    for i in range(-t, t+1):
        for j in range (-t,t+1):
            if i==0 and j==0:
                continue
        I2_=I2[padLength+i-f:padLength+i+f+height,padLength+j-f:padLength+j+f+width]  # 移动的领域窗口x
        w = np.exp(-cv2.filter2D((I2_ - I_)**2, -1, kernel)/h)[f:f+height, f:f+width]  # 计算权重w，保持形状
        sweight += w  # 将所有的权值相加
        wmax=np.maximum(wmax,w)  # 求最大
        average += (w*I2_[f:f+height,f:f+width])  # 得到权值与窗口x相乘的值并求和
    I2=(average+wmax*I)/(sweight+wmax)  # 权值最大的是自身
    return np.clip(np.round(I1),0,255).astype(L.dtype)

上述计算过程实际上是：
设含噪声图像为v，去噪后的图像为u。u中像素点x处的灰度值通过如下方式得到：

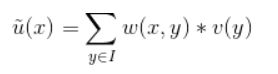
其中权值w表示像素点x和y间的相似度，它的值由以V(x)、V(y)为中心的矩形邻域间的距离决定：

Z(x)为归一化系数，h为平滑参数，控制高斯函数的衰减程度。h越大高斯函数变化越平缓，去噪水平越高，但同时也会导致图像越模糊。h越小，边缘细节成分保持得越多，但会残留过多的噪声点。h的具体取值应当以图像中的噪声水平为依据。

(三）代码实现

附上完整代码：

import cv2
import numpy as np

def psnr(A,B):
    val=255
    mse=((A.astype(np.float)-B)**2).mean()
    return 10*np.log10((val*val)/mse)

def double2unit8(I,L,ratio=1.0,sigma=20.0):
    I=I.astype(np.float64)  # 转换成float形式便于计算
    noise=np.random.randn(*I.shape)*sigma  # 生成的时形状与I相同，均值为0，标准差为sigam的随机高斯噪声矩阵
    noisy=I+noise # 噪声图像
    return np.clip(np.round(noisy*ratio),0,255).astype(L.dtype) # 转换回图像的unit8均值

def make_kernel(f):   # 计算得到一个高斯核，用于后续的计算
    kernel=np.zeros((2*f+1,2*f+1))
    for d in range(1,f+1):
        kernel[f-d:f+d+1,f-d:f+d+1] += (1.0/((2*d+1)**2))
    return kernel/kernel.sum()

def NLmeansfilter(I,L,h_=10,templateWindowSize=5,searchWindowSize=11):
    I=I.astype(np.float64)
    f=int(templateWindowSize/2)
    t=int(searchWindowSize/2)
    height,width=I.shape[:2]  # 利用ndarray的索引得到长宽
    padLength=t+f
    I2=np.pad(I,padLength,'symmetric')  # 
    kernel=make_kernel(f)
    h=(h_**2)
    I_=I2[padLength-f:padLength+f+height,padLength-f:padLength+f+width]
 
    average=np.zeros(I.shape)
    sweight=np.zeros(I.shape)
    wmax=np.zeros(I.shape)
    for i in range(-t, t+1):
        for j in range (-t,t+1):
            if i==0 and j==0:
                continue
        I2_=I2[padLength+i-f:padLength+i+f+height,padLength+j-f:padLength+j+f+width]
        w = np.exp(-cv2.filter2D((I2_ - I_)**2, -1, kernel)/h)[f:f+height, f:f+width]
        sweight += w
        wmax=np.maximum(wmax,w)
        average += (w*I2_[f:f+height,f:f+width])
    I1=(average+wmax*I)/(sweight+wmax)
    return np.clip(np.round(I1),0,255).astype(L.dtype)

if __name__=='__main__':
    I=cv2.imread('E:\opencv\long.jpg',0)  # 以灰度图像形式读取
    sigma=20.0
    I1=double2unit8(I,I,sigma=20.0)  # 对图像加上高斯噪声
    R2 = cv2.fastNlMeansDenoising(I1, None, sigma, 5, 11)  # 利用opencv自带的NLM去噪
    R1=NLmeansfilter(I,I, sigma, 5, 11)  # 自定义去噪
    cv2.imshow("Image",I)
    cv2.imshow("noisy",I1)
    cv2.imshow("NLM",R1)
    cv2.imshow("fastNLM",R2)
    print ('噪声图像PSNR',psnr(I, I1))
    print ('CV去噪PSNR',psnr(I,R2))
    print ('NLM去噪PSNR',psnr(I,R1))
    cv2.waitKey(0)  #显示图像必备
    cv2.destroyALLWindows()  #释放窗口 

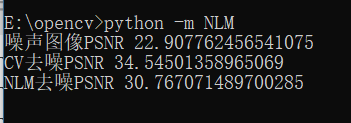
实际上凭肉眼来看，我觉得自定义的NLM效果更好一i点，但是从PSNR结果上来看确实CV自带的函数效果更好。这是因为PSNR是最普遍和使用最为广泛的一种图像客观评价指标，然而它是基于对应像素点间的误差，即 基于误差敏感的图像质量评价由于并未考虑到人眼的视觉特性（人眼对空间频率较低的对比差异敏感度较高，人眼对亮度对比差异的敏感度较色度高，人眼对一个 区域的感知结果会受到其周围邻近区域的影响等），因而经常出现评价结果与人的主观感觉不一致的情况。

同时结合之前学到的一些去噪方法进行对比实验：

if __name__=='__main__':
    I=cv2.imread('E:\opencv\long.jpg',0)  # 以灰度图像形式读取
    sigma=20.0
    I1=double2unit8(I,I,sigma=20.0)  # 对图像加上高斯噪声
    R2 = cv2.fastNlMeansDenoising(I1, None, sigma, 5, 11)  # 利用opencv自带的NLM去噪
    R1=NLmeansfilter(I,I, sigma, 5, 11)  # 自定义去噪
    dst2=cv2.ximgproc.guidedFilter(guide=I,src=I1,radius=8,eps=200,dDepth=-1)
    img=cv2.medianBlur(I1,5)
    gaussian=cv2.GaussianBlur(I1,(5,5),1.5)
    cv2.imshow("Image",I)
    cv2.imshow("noisy",I1)
    cv2.imshow("NLM",R1)
    cv2.imshow("fastNLM",R2)
    cv2.imshow("guided",dst2)
    cv2.imshow("median",img)
    cv2.imshow("GaussianBlur",gaussian)
    print ('噪声图像PSNR',psnr(I, I1))
    print ('CV去噪PSNR',psnr(I,R2))
    print ('NLM去噪PSNR',psnr(I,R1))
    print('guided图像去噪PSNR',psnr(I,dst2))
    print('median去噪PSNR',psnr(I,img))
    print('高斯去噪PSNR',psnr(I,gaussian))
    cv2.waitKey(0)  #显示图像必备
    cv2.destroyALLWindows()  #释放窗口 

引导滤波效果真心不错：

参考链接：
图像质量评估
非局部均值滤波的python实现