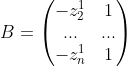灰色预测模型GM(1,1)概述+模型推导+Matlab实现案例
灰色预测GM(1,1)可以用来进行小样本的未来预测(外部预测 )，例如SARS的传播问题、长江水质的评价与预测、艾滋病疗法的评价与预测、高教学费标准探讨问题等等。
一、灰色模型概念
1.系统
客观世界在不断发展变化的同时，往往通过事物之间及因素之间相互制约、相互联系而构成一个整体，我们称之为系统。
2.白色系统
从信息的完备性与模型的构建上看，工程技术等系统具有较充足的信息量，其发展变化规律明显，定量描述较方便，结构与参数较具体，人们称之为白色系统。
3.灰色系统
对另一类系统诸如社会系统、农业系统、生态系统等，人们无法建立客观的物理原型，其作用原理亦不明确，内部因素难以辨识或之间关系隐蔽，人们很难准确了解这类系统的行为特征，因此对其定量描述难度较大，带来建立模型的困难。这类系统内部特性部分已知的系统称之为灰色系统。
4.黑色系统
一个系统的内部特性全部未知，则称之为黑色系统。
5.灰色系统与白色系统的区别
区别白色系统与灰色系统的重要标志是系统内各因素之间是否具有确定的关系。运动学中物体运动的速度、加速度与其所受到的外力有关，其关系可用牛顿定律以明确的定量来阐明，因此，物体的运动便是一个白色系统。
6.灰色系统的建模基础
•灰色系统理论建模的主要任务是根据具体灰色系统的行为特征数据，充分开发并利用不多的数据中的显信息和隐信息，寻找因素间或因素本身的数学关系。通常的办法是采用离散模型，建立一个按时间作逐段分析的模型。但是，离散模型只能对客观系统的发展做短期分析，适应不了从现在起做较长远的分析、规划、决策的要求。尽管连续系统的离散近似模型对许多工程应用来讲是有用的，但在某些研究领域中，人们却常常希望使用微分方程模型。事实上，微分方程的系统描述了我们所希望辨识的系统内部的物理或化学过程的本质。
•灰色系统理论首先基于对客观系统的新的认识。尽管某些系统的信息不够充分，但作为系统必然是有特定功能和有序的，只是其内在规律并未充分外露。有些随机量、无规则的干扰成分以及杂乱无章的数据列，从灰色系统的观点看，并不认为是不可捉摸的。相反地，灰色系统理论将随机量看作是在一定范围内变化的灰色量，按适当的办法将原始数据进行处理，将灰色数变换为生成数，从生成数进而得到规律性较强的生成函数。例如，某些系统的数据经处理后呈现出指数规律，这是由于大多数系统都是广义的能量系统，而指数规律是能量变化的一种规律。
•灰色系统理论的量化基础是生成数，从而突破了概率统计的局限性，使其结果不再是过去依据大量数据得到的经验性的统计规律，而是现实性的生成律。这种使灰色系统变得尽量清晰明了的过程被称为白化。
二、生成数列
灰色系统理论把一切随机量都看作灰色数---即在指定范围内变化的所有白色数的全体。对灰色数的处理不是找概率分布或求统计规律，而是利用数据处理的办法去寻找数据间的规律。通过对数列中的数据进行处理，产生新的数列，以此来挖掘和寻找数的规律性的方法，叫做数的生成。
1.累加生成数列AGO（Accumulated Generating Operation）
把数列 x 各时刻数据依次累加的过程叫做累加过程，记作 AGO，累加所得的新数列，叫做累加生成数列。
设原始数列为
.
令
,
则原数列的一次累加生成数列为
.
累加生成特点
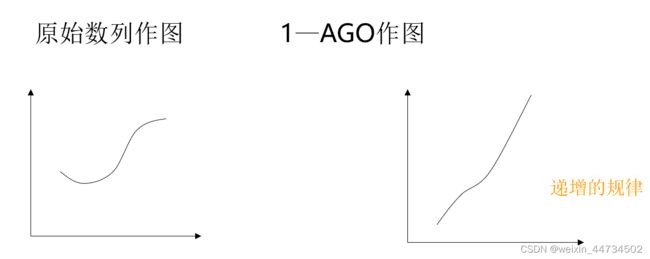
一般经济数列都是非负数列。累加生成能使任意非负数列、摆动的与非摆动的，转化为非减的、递增的。如图1所示。
图1
累加生成模型
经累加生成后，如果有较强的规律，并且接近某一函数，则该函数成为生成函数。生成函数就是一种模型，称为生成模型。通过累加获得的模型称为累加生成模型。如图2所示。
图2
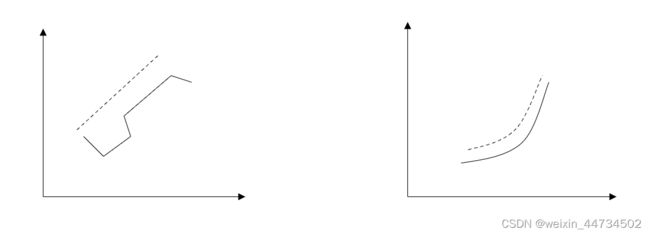
2.累减生成数列
如果原始数列为
，
令
则称
为数列
的1词累减生成数列。
3.均值生成数列
设原始数列为
，
对常数
![\alpha \epsilon [0,1]](http://img.e-com-net.com/image/info8/e80fc5c376ee473ba4310444c3735f36.gif){kind=small}
,
为由数列在权
下生成的邻值生成数列。
二、模型推导
设原始数列为
.
令
,
则原数列的一次累加生成数列为
.
均值生成数列为
于是灰微分方程为
相应白化微分方程为
记
,
最小二乘法求得
于是解白化方程得
.
三、实例
clc,clear
x0=[71.1 72.4 72.4 72.1 71.4 72.0 71.6];
n=length(x0);
lamda=x0(1:n-1)./x0(2:n)
range=minmax(lamda)
x1=cumsum(x0)
for i=2:n
z(i)=0.5*(x1(i)+x1(i-1));
end
B=[-z(2:n)',ones(n-1,1)];
Y=x0(2:n)';
u=B\Y
x=dsolve('Dx+a*x=b','x(0)=x0');
x=subs(x,{'a','b','x0'},{u(1),u(2),x1(1)});
yuce1=subs(x,'t',[0:n-1]);
digits(6),y=vpa(x) %为提高预测精度，先计算预测值，再显示微分方程的解
yuce=[x0(1),diff(yuce1)]
epsilon=x0-yuce %计算残差
delta=abs(epsilon./x0) %计算相对误差
rho=1-(1-0.5*u(1))/(1+0.5*u(1))*lamda %计算级比偏差值
2.
Matlab代码
clc,clear
han1=[83.0 79.8 78.1 85.1 86.6 88.2 90.3 86.7 93.3 92.5 90.9 96.9
101.7 85.1 87.8 91.6 93.4 94.5 97.4 99.5 104.2 102.3 101.0 123.5
92.2 114.0 93.3 101.0 103.5 105.2 109.5 109.2 109.6 111.2 121.7 131.3
105.0 125.7 106.6 116.0 117.6 118.0 121.7 118.7 120.2 127.8 121.8 121.9
139.3 129.5 122.5 124.5 135.7 130.8 138.7 133.7 136.8 138.9 129.6 133.7
137.5 135.3 133.0 133.4 142.8 141.6 142.9 147.3 159.6 162.1 153.5 155.9
163.2 159.7 158.4 145.2 124.0 144.1 157.0 162.6 171.8 180.7 173.5 176.5];
han1(end,:)=[];m=size(han1,2);
x0=mean(han1,2);
x1=cumsum(x0);
alpha=0.4;n=length(x0);
z1=alpha*x1(2:n)+(1-alpha)*x1(1:n-1)
Y=x0(2:n);B=[-z1,ones(n-1,1)];
ab=B\Y
k=6;
x7hat=(x0(1)-ab(2)/ab(1))*(exp(-ab(1)*k)-exp(-ab(1)*(k-1)))
z=m*x7hat
u=sum(han1)/sum(sum(han1))
v=z*u