手把手教你写评分函数以及SVM损失函数和SoftMax损失函数

 

小时候，我们在学习的过程中，也可以认为是一个摸索的过程，不断犯错并且一点点修正的过程；通俗地讲，计算机训练模型的过程，也是一个如人一样学习的过程，每一次模型的训练就是一次尝试，这次尝试都会得出一个结果数值，用来得出这个结果数值的函数称之为评分函数(score function)；如小时候做错事情一样，犯错越大，就会得到越大的惩罚，计算机评估犯错程度大小的函数称之为代价函数(cost function)，有些地方也称为损失函数(loss function)；如教育小孩子一般，不断地去修正错误，最终得到较为正确的行为，在计算机中类似的方法称为梯度下降(gradient descent)。

1 评分函数

这一小节将完成一个线性分类器的评分函数，获取一个随机的未进行训练模型的分数。首先看一下线性分类器的评分函数的原理。

前面已经知道一副图像可以看做是一个3027维的向量，而CIFAR-10图像分类的结果共有10个可能，也就是说，评分函数输入一个为3027维的向量，最终得出一个10维的向量，这10维向量中十个数字代表各个类别的分类评分，当然，10个得分中的最高得分对应的类别会被认为是分类结果。获取分数的计算过程，即评分函数，如式1所示。

                            式1

其中，f(X)为最终的到的分数，W为10*3027的矩阵，X为某副输入图像的转置，即单幅图像的大小为1*3027的向量，其转置为3027*1，这样W与X相乘的结果为10*1的矩阵；最后在将相乘结果加上一个偏执B，同样为10*1大小的矩阵，得到最终的分数。比对10个得分，最高分数为该类别。

一个随机的W和B实现CIFAR-10分类

在这一小节，先不对W和B的含义以及如何得到合适的W和B的方法进行探讨。先写一个程序，随机获取一个W和B进行分类，也可以认为是计算机的瞎蒙，看一看最终结果。程序如1所示。

程序1 一个随机的W和B实现CIFAR-10分类

import pickle
import os
import numpy as np

n = 2

def unpickle_as_array(filename):
    with open(filename, 'rb') as f:
        dic = pickle.load(f,encoding='latin1')
        dic_data = dic['data']
        dic_labels = dic['labels']
        dic_data = np.array(dic_data).astype('int')   
        dic_labels = np.array(dic_labels).astype('int')  
        return dic_data, dic_labels

def load_batches(root,n):
    train_data = []
    train_labels = []
    for i in range(1,n+1,1):
        f = os.path.join(root,'data_batch_%d' %i)
        data, labels = unpickle_as_array(f)
        train_data.append(data)
        train_labels.append(labels)
    train_data_r = np.concatenate(train_data)   
    train_labels_r = np.concatenate(train_labels)
    del train_data, train_labels
    test_data, test_labels = unpickle_as_array(os.path.join(root, 'test_batch'))
    return train_data_r, train_labels_r, test_data, test_labels

w = np.random.rand(10,3072)
b = np.random.rand(10)
train_data, train_labels, test_data, test_labels = load_batches('E:/cifar/cifar-10-batches-py', n)
result = np.zeros(10000)
for i in range(1000):
    score = w.dot(test_data[i,:])+b
    result[i] = np.argmax(score)
print('the algorithm\'s accuracy: %f' % (np.mean(result == test_labels)))

程序1 的30行以前代码参考https://blog.csdn.net/qq_36552550/article/details/105835108。

30以及31行得到随机矩阵w和b，32行读入图像数据；然后，通过for语句循环读入测试集中的10000副图像，因为每次只对一副图像进行计算，所以要读入的大小为10000*3072的test_data进行切片操作——test_data[i,:]，得到第i张图片；计算得到评分score，通过argmax()函数找到最大的那个数对应的下标赋值给result[i]，获取到这一副图像的分类。

注意：这里test_data[i,:]并没有进行转置，因为在python中，test_data[i,:]为array类型，它的shape属性为(3072,)，简单地讲，它既可以认为是线性代数中的行向量，也可以认为是列向量。在进行计算的时候，它会自动匹配矩阵进行运算；当然，这里将w.dot(test_data[i,:])改为w.dot(test_data[i,:].T)，其结果是一致的。

最后，37行将分类结果与测试集的正确结果比对，得出准确率，因为是随机获得的w和b，每次结果都不一样，但根据概率来讲，其结果都应趋近于0.10。随机的一次运行结果如1所示。

图1 随机的w和b进行评分的准确率结果

评分函数的理解

这里先以二维为例，看一简单的例子，如图5-4-2所示，xd1表示横轴，xd2表示纵轴；图中叉点、圆点以及方块是三个类别，三条直线分别将三个类别分开，红线判别星点，蓝线判别方块，黄线判别圆点。如何得到正确的“分类线”会在后面进行学习。

注意：从这里可以看出，偏执B的作用，如果没有偏执B，那么所有的“分类线”都过原点，如果一个点位于原点位置，那么它的所有分类得分都为0。

以红线判别一个新的点是否为星点为例，若一个新的点为(x1,x2)位于红线上面，那么它的判定得分就是0，沿着红线的箭头方向，得分不断地增加；沿着红线箭头反方向，则得分不断地减少。

图2 二维空间下三分类示例

那么，对于一副图像来讲，3072个数值（32*32*3）可以看做是一个3072维空间下的一个点。而矩阵W和B则类似于图5-4-2中的“分类线”一般。

通过后面的小节，可以得出正确的矩阵W（假定这里已经提前得出了正确矩阵）。将矩阵W缩放到0至255区间，将矩阵W对应的horse马分类和ship船分类的那一行提取出来；然后将其进行图片可视化，如图3所示。

 

图3 矩阵W的马（左图）和船（右图）分类可视化

可以看出，马分类的图片隐约可以看到一匹马，但是马似乎有两个头，这是因为数据库里面的马图片既可能左边站立，也可能朝右边站立，所以在中间位置给与马的棕红色较大的权重，同时，因为马匹可能左右站立，所以两种可能都给与了较大权重。

而船分类的图片，图片大多呈现蓝色，因为船的图片大多在海面上，而海面大多是蓝色，所以给与蓝色特别大的权重，中间部位则隐约是一个白色的船只，则中间给与白色较大的权重。也就是说，矩阵W中船分类对应的那一行数字，对应于图片像素中RGB值，其中B值的地方，数值大多较高，而R值和G值则较低。可以想象，如果一副新的图片，整体呈现蓝色，而中间是白色的物体，那么进行计算，这幅图片在分类的时候，船分类对应的得分肯定会特别高。

评分函数的简写

式1可以简写——省略偏执B。如何省略偏执B呢？对于CIFAR-10来讲，W为10*3072的矩阵，只需将偏执B放在W矩阵的最后一列即可，新的W为大小为10*3073的矩阵，而Xi为第i副图像，其转置为3072*1列向量，只需在最后一行3072行后面在加一行，将其数值固定为1，这样新的Xi为大小为3073*1的列向量。并且计算结果和式1完全一致。最终可以简写为式2。

式2

2 损失函数

犯错有大有小，计算机里面猜错了分类，也会进行评估错误的程度；评估错误大小的函数叫做损失函数（loss function），有些地方也有叫做代价函数（cost function）。错的离谱，那么损失函数的计算结果分值就大；反之，猜的很正确，那么损失函数计算结果分值就很小。

损失函数的实现有多种方法，这里面介绍两种方法——SVM（Support Vector Machine）支持向量机以及SoftMax。

SVM

在CIFAR-10分类的训练中，通过目标函数获取到第i副图像xi的十个类别的得分，其中正确标签类别对应的得分为syi，其他的类别j的得分为sj；支持向量机的核心思想是让正确标签类别对应的得分syi比sj其他类别的得分多 ∆ 。

对于第i副训练集图像进行分类，SVM代价函数的计算如式3所示。

可以看出，正确标签类别对应的得分syi比sj其他类别的得分多 ∆ 时候，小于0，此时0和比对，最大值为0；因为训练集的一副图像在十个类别里面有一个是正确的，其他九个是非正确的，所以，需要计算9次，然后求和得到最终的SVM损失函数结果。

除此之外，SVM代价函数还需要加入正则化项regularization以便对W进行限制，得出唯一的W。可以想象，如果一个的W能够正确地分类所有的图像，那么其损失函数的结果为0，而使一个λ>1，λW对图像进行分类，依旧为能够满足损失函数的结果为0。这样W就不是唯一的。

所以，对所有的训练图像（并非仅仅对第i副通过损失函数求结果）通过损失函数求结果，并求和；然后加入正则化项，如式4所示。

其中，加号前半部分对所有训练集图像进行计算后求和，N为训练集图像的数量；后半部分为正则化项，对矩阵W每一个元素（即第r行第c列的元素）进行求平方然后全部相加，并乘以参数λ，得出正则化项的结果。

注意：这里的正则化项W不需要包含偏执项B！

然后，通过Python来编写一个SVM损失函数，并对一个随机的W和B，通过SVM损失函数计算最终结果，程序如2所示，注意该程序未加入正则化项。

程序2 SVM损失函数实现

import pickle
import os
import numpy as np
from numpy import random,mat
n = 2

def unpickle_as_array(filename):
    with open(filename, 'rb') as f:
        dic = pickle.load(f,encoding='latin1')
        dic_data = dic['data']
        dic_labels = dic['labels']
        dic_data = np.array(dic_data).astype('int')
        dic_labels = np.array(dic_labels).astype('int')
        return dic_data, dic_labels

def load_batches(root,n):
    train_data = []
    train_labels = []
    for i in range(1,n+1,1):
        f = os.path.join(root,'data_batch_%d' %i)
        data, labels = unpickle_as_array(f)
        train_data.append(data)
        train_labels.append(labels)
    train_data_r = np.concatenate(train_data)
    train_labels_r = np.concatenate(train_labels)
    del train_data, train_labels
    test_data, test_labels = unpickle_as_array(os.path.join(root, 'test_batch'))
    return train_data_r, train_labels_r, test_data, test_labels

def svm_loss(x, y, W, n):
    delta = 1.0
    loss = np.zeros(10000 * n)
    for i in range(10000 * n):
        scores = W.dot(x[i])
        margins = np.maximum(0, scores - scores[y[i]] + delta)
        margins[y[i]] = 0
        loss[i] = np.sum(margins)
        #print('the %fth image\'s svm_loss is %f ' % (i,loss[i]))
    total_loss = np.sum(loss)
    return total_loss

w = np.random.rand(10,3072)
b = np.random.rand(10,1)
W = np.concatenate((w,b),1)
print(W.shape)
train_data, train_labels, test_data, test_labels = load_batches('E:/cifar/cifar-10-batches-py', n)
tail_1 = np.ones((n*10000,1))
train_data = np.concatenate((train_data,tail_1), 1)
print(train_data)
t_loss = svm_loss(train_data, train_labels, W, n)
print(t_loss)

30行代码至40行实现了对n个训练集的图像数据通过SVM损失函数计算结果。函数名为svm_loss，其参数分别为训练集图像数据x，训练集图像的标签y，以及目标函数中的W（这里的W包含偏执B），n表示读入了几个数据集文件。

这里将式3的∆值设置为1，即第31行代码。 loss存储了10000*n副训练集图像对应的损失函数计算的值。这里可以思考一下∆值的设置，例如的差值如果较大——大多数情况下都远大于100的话，那么∆值设置为100或者1对最终结果关系不大。

34至37行代码实现了式5-4-3的计算；训练集的一副图像在十个类别里面有一个是正确的，其他九个是非正确的，所以，只需要计算非正确类别的9次；在第36行将正确类别对应的计算结果置零，来实现这九次计算，而非十次计算。最终将所有训练集图像的损失函数计算结果相加。

回顾“评分函数的简写”这一小节我们知道，要将矩阵W和B进行简化。41至43行，随机创建了W矩阵和B矩阵，然后将B矩阵添加在W矩阵的后面，注意是横向添加矩阵，所有concatenate()函数的第二个参数是1，而不是0。然后，要在输入图像3072个元素后面追加一个元素1，47行至48行完成了该过程。此时，矩阵W大小应该为10*3073，而10000*2个训练集的图像原本读出后，其图像数据的矩阵大小为20000*3072，所有图像最后都加上一个1后，新的图像数据的矩阵大小为20000*3073。

50行计算出结果并输出。一次随机的运行结果如图4所示。

图4 SVM损失函数运行结果示意图

通过SVM的损失函数得出结果后，要做的就是让计算机“犯得错误小”，即通过改变矩阵W让这个最终的损失函数得出的总的和值让其尽量的小，不断改变矩阵W最终使得损失函数的结果值最小化的方法叫做梯度下降。

在进行梯度下降的学习前，先看另一种常用的损失函数——SoftMax分类器的损失函数，该损失函数也用于卷积神经网络。

SoftMax

SVM的损失函数可以看出只要正确标签类别对应的得分syi比sj其他类别的得分多 ∆就可以得到0的结果；但如果syi比sj多更多，即远大于 ∆，则结果依旧也为0，也就是说SVM损失函数只关心这个W有多差，而不关心W有多优秀。而SoftMax损失函数则同时兼顾两个方面。

SoftMax和SVM在评分函数的步骤相同，都需要通过式5-4-1得出分数；但后面的计算不同。

对于CIFAR-10而言，每幅图片对应10个类别，若将一副的图像进行分类测试，SoftMax分类器将得出10个类别分类的各自概率，即10个0至1的数值（10个数值相加为1）。

那么，如果模型合理，那么图像真实类别的概率应该接近1，即接近100%，而其他错误类别的概率应接近0。这种合理的模型，其损失函数结果应该尽量小。

反之，如果通过模型进行分类，图像真实的类别概率判定很小，那么这个模型肯定很不合理，那么损失函数结果应该尽量的大，表明模型“犯错”程度高。

SoftMax的损失函数如式5所示。

前面评分函数可对一副图像得出所有类别的评分，SoftMax损失函数第一步要得出正确类别评分占据总评分的概率。

Li表示训练集第i幅图像的损失函数结果，fyi表示第i幅图像正确的类别对应的评分，fj表示该图像第j个类别的评分函数结果，则表示所有类别的之和。表示正确类别的分类概率。

合理的分类，的值应该趋近于1，而越是不合理的分类，越趋近于0；log函数则特别适合作为概率分类的损失函数计算。

 

通过图5可以看出，选取a大于1时，当logax中的x趋近于0时，y趋近于无穷；当x趋近于1时，y趋近于0。

图5 -logax a>1函数图

而a选取自然数e，从后面可以看到选取自然数e时，一些包含自然数e的式子求导特别方便。

根据式5编写程序，通过SoftMax的损失函数计算一个随机的W（包含偏执B）的结果并显示，如程序3所示。

程序3 SoftMax损失函数实现

import pickle
import os
import numpy as np
from numpy import random,mat
n = 2

def unpickle_as_array(filename):
    with open(filename, 'rb') as f:
        dic = pickle.load(f,encoding='latin1')
        dic_data = dic['data']
        dic_labels = dic['labels']
        dic_data = np.array(dic_data).astype('int')
        dic_labels = np.array(dic_labels).astype('int')
        return dic_data, dic_labels

def load_batches(root,n):
    train_data = []
    train_labels = []
    for i in range(1,n+1,1):
        f = os.path.join(root,'data_batch_%d' %i)
        data, labels = unpickle_as_array(f)
        train_data.append(data)
        train_labels.append(labels)
    train_data_r = np.concatenate(train_data)
    train_labels_r = np.concatenate(train_labels)
    del train_data, train_labels
    test_data, test_labels = unpickle_as_array(os.path.join(root, 'test_batch'))
    return train_data_r, train_labels_r, test_data, test_labels

def softmax_loss(x, y, W, n):
    loss = np.zeros(10000 * n)
    for i in range(10000 * n):
        scores = W.dot(x[i])
        scores -= np.max(scores)
        p = np.zeros(10)
        p = np.exp(scores) / np.sum(np.exp(scores))
        print(p)
        loss[i] = - np.log(p[y[i]])
    total_loss = np.sum(loss)
    return total_loss

np.set_printoptions(suppress=True)
w = np.random.rand(10,3072)
b = np.random.rand(10,1)
W = np.concatenate((w,b),1)
train_data, train_labels, test_data, test_labels = load_batches('E:/cifar/cifar-10-batches-py', n)
tail_1 = np.ones((n*10000,1))
train_data = train_data/255
train_data = np.concatenate((train_data,tail_1), 1)
t_loss = softmax_loss(train_data, train_labels, W, n)
print(t_loss)

这里需要注意两点，48行程序将图像的数值全部除以255，因为在计算e的scores次方时，数值可能太大，超出Python的数值范围。

同样为了防止数值过大，在编写程序的时候，将式5改为式6，最终结果不变；fmax为评分函数结果中10个评分最大的那个数。这样分子分母中e的次方都为小于等于0，即分子分母的值都小于等于1。

式6

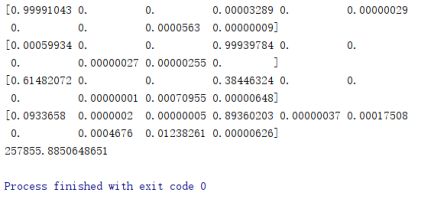
一次随机的运行结果部分截图如图6所示。

图6 SoftMax损失函数运行结果截图