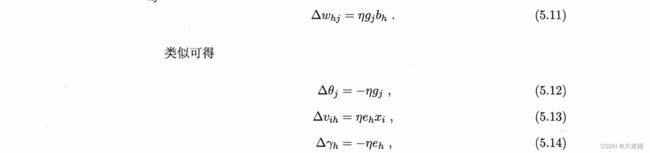机器学习_西瓜书_C5神经网络

目录

5.1 神经网络 neural network

原理

流程

激活函数 activation function

5.2 分类

感知机 Perception 

单层(w/o 隐含层)

多层(with 隐含层hidden layer)

误差逆传播(BP) error BackPropagation

全局最小(global minimum) vs 局部极小(local minimum)

其它神经网络

径向基函数 RBF网络 (radial basis function) 单隐层, 前馈神经网络

自适应谐振理论 ART网络 (adaptive resonance theory) 竞争型学习, 结构自适应网络

自组织映射 SOM网络 (self-organizing map) 竞争型学习

级联相关网络 (cascade-correlation) 结构自适应网络(可调整)

Elamn网络 递归神经网络

Boltzman机 递归神经网络

5.3 深度学习Deep ~/特征学习Feature ~/表示学习Representation ~

目标

方法

TASK4 学习心得

---

5.1 神经网络 neural network

原理

神经元neuron"兴奋"时超过阈值threshold被激活, 向其它神经元传递信号.

流程

1. 输入: i个x加权
2. 处理: if 激活函数Σwx > threshold
3. 输出: y = f(Σwx - θ)

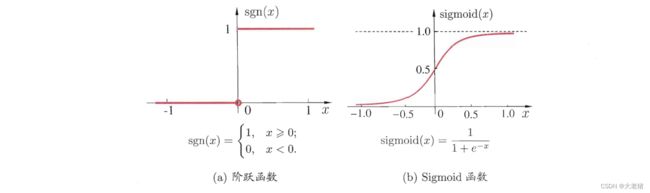
激活函数 activation function

• (×) 阶跃函数: 非连续, 不光滑 y = 0 or 1
• (√) sigmoid函数(squashing f): 连续, 光滑 y∈[0,1]

5.2 分类

• M-P模型 (本章重点介绍)
  • 感知机
  • 误差逆传播
• 径向基函数 RBF网络 (radial basis function)
• 自适应谐振理论 ART网络 (adaptive resonance theory)
• 自组织映射 SOM网络 (self-organizing map)
• 级联相关网络 (cascade-correlation)
• 递归神经网络-Elamn网络 (recurrent neural network)
• 基于能量模型-Boltzman机 (energy-based model)

感知机 Perception 

单层(w/o 隐含层)

输入层: 传递signal

输出层: M-P神经元(阈值逻辑单元threshold logic unit)

线性可分(linearly separable): 学习过程一定会收敛converge, 从而得到w权向量

与AND (x1∧x2), w1=w2=1, θ=2, y=(w1x1+w2x2-θ)=(x1+x2-2)→当且仅当x1=x2=1时,y=1

或OR (x1∨x2), w1=w2=1, θ=0.5, y=(w1x1+w2x2-θ)=(x1+x2-0.5)→当x1=1或x2=1时,y=1

非NOT (¬1), w1=-0.6, w2=0, θ=-0.5, y=(w1x1+w2x2-θ)=(-0.6x1+0.5)→当x1=1时y=0, x1=0时y=1

可将阈值θ视为固定值-1.0的哑结点dummy node, 使阈值θ和权重w的学习→仅对权重w的学习

w_i = w_i + Δw 预测正确Δ=0, w_i不变

Δw_i = η * ( y - y_hat ) * x_i 学习率learning rate(η)

线性不可分: 学习过程会震荡fluctuation, 不能求得合适解 → 考虑多层

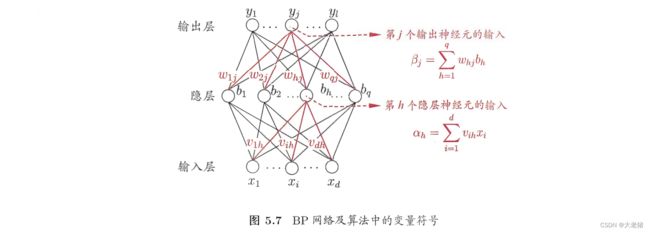
多层(with 隐含层hidden layer)

多层前馈神经网络multi-layer feedforward 前馈指的是不存在loop or return

1. 输入层: only input, NO process
2. 隐含层: process 包含功能神经元
3. 输出层: process+output 包含功能神经元

误差逆传播(BP) error BackPropagation

适用: 多层前馈神经网络(most), 递归神经网络

 

标准BP: 随机梯度下降 stochastic ~

MIN(single error) → 迭代 → SUM

优:下降快,适合big dataset

缺: 迭代频繁

累积BP: 标准梯度下降

MIN(SUM error)

优:迭代少

缺:一定程度后下降缓慢, 建议改为标准BP

How to set hidden layer?

Trial-by-error 试错法

How to avoid overfitting? 

1. Early stopping: D=训练集+验证集, if error训练↓, error验证↑, then STOP
2. Regularization: use λ∈(0,1) to reconcile 检验误差&网络复杂度, 常用交叉验证法估计

全局最小(global minimum) vs 局部极小(local minimum)

Solution

• 改起点: 以多组不同参数开始
• 改中点: 模拟退火(simulated annealing) 每一步接收次优解
• 改方法: 随机梯度下降 → final slope≠0 → continue
• 遗传算法(genetic algorithm)

其它神经网络

径向基函数 RBF网络 (radial basis function) 单隐层, 前馈神经网络

步骤

1. 确定神经元中心 by 随机采样, 聚类;
2. 确定参数 w, β

自适应谐振理论 ART网络 (adaptive resonance theory) 竞争型学习, 结构自适应网络

竞争型学习: 胜者通吃 winner-take-all

1. 比较层: 接收样本, 传递
2. 识别层: 神经元match模式 one by one, 数量可动态增长
3. 竞争: 取 MIN(distance(输入向量, 代表向量)),
4. if d>识别阈值, 归为该类; if ≤, 重置模块新增一个神经元

识别阈值↑, 模式类别多, 精细; ↓, 类别少, 粗略

优: 缓解了竞争性学习的"可塑性(学新)-稳定性(忆旧)dilemma"; 可进行增量学习, 在线学习

分类: 早期ART-Boolean only; ART2-实值; FuzzyART-模糊值; ARTMAP-监督学习

自组织映射 SOM网络 (self-organizing map) 竞争型学习

可将高维数据映射到低维, 同时保持拓扑结构

原理: 输出层以矩阵方式排列, 每个神经元一个权向量, 训练目标就是为每个输出层神经元找到合适权向量, 保持拓扑结构

过程

1. 最佳匹配单元 = MIN(d(样本, 权向量))
2. adj d(最佳匹配单元, 权向量)
3. 迭代iterate→converge

级联相关网络 (cascade-correlation) 结构自适应网络(可调整)

可变: 连接权w, 阈值, +网络结构

"级联": +新隐层神经元

"相关": MAX(correlation(神经元输出, 网络误差)) → 训练参数

优: (×) set 网络层num, 隐层神经元num; 训练速度较快

缺: dataset小容易overfitting

Elamn网络 递归神经网络

递归神经网络(Recurrent NN): 允许环形网络with loop

结构: 类似多层前回馈, 但return隐层输出as next input

隐层用sigmoid激活函数, 网络训练用BP算法

Boltzman机 递归神经网络

基于能量模型 (energy-based model), MIN(f(energy))

1. 显层-输入
2. 隐层Boolean: 0抑制/1激活
3. 显层-输出

目标: MAX(P(状态向量s出现概率))

标准Boltzman机: 全连接

restricted Boltzman机: only save 显层~隐层, 用对比散度CD训练

CD: 先算隐层概率分布, 采样; 后更新连接权

5.3 深度学习Deep ~/特征学习Feature ~/表示学习Representation ~

模型复杂度高, 体量capacity大

目标

体量↑

方法

1. DBN深度信念网络: 隐层num↑→神经元num↑,层数↑
   • 缺点: 标准BP算法failure, 会导致误差发散diverge无法收敛converge
   • 解决: 无监督逐层训练, "预训练+微调": 局部寻优→全局寻优
   • 过程: 每一层都按照Restricted Boltzman机(RBM)训练, 上层output→本层input→本层output→下层input
2. CNN卷积神经网络
   1. 特征映射feature map: 采样层亚采样to data↓ & save info
   2. 权共享: 一组神经元使用相同连接权 

---

TASK4 学习心得

• Gradient decent note from 吴恩达老师ML_week1
• Code忘完了, 要结合课件回忆一下
• 之前学code算neuron还会晕, 现在不会了, 嗯真好googood