python雷达成像（SAR）仿真：（三）徙动校正+方位压缩（完结）

import numpy as np
import math
import cmath
import pylab
import time
from matplotlib import pyplot as plt

##时间统计
time_start = time.time()

pylab.mpl.rcParams['font.sans-serif'] = ['SimHei']
pylab.mpl.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
## 参数设置
##--------------------------------------------------------------------
##定义参数
R_nc = 20e3  # 景中心斜距
Vr = 150  # 雷达有效速度
Tr = 2.5e-6  # 发射脉冲时宽
Kr = 20e12  # 距离调频率
f0 = 5.3e9  # 雷达工作频率
BW_dop = 80  # 多普勒带宽
Fr = 60e6  # 距离采样率
Fa = 200  # 方位采样率
Naz = 512  # 距离线数（即数据矩阵，行数）——这里修改为1024。
Nrg = 512  # 距离线采样点数（即数据矩阵，列数）
sita_r_c = (0 * np.pi) / 180  # 波束斜视角，0 度，这里转换为弧度
c = 3e8  # 光速

R0 = R_nc * np.cos(sita_r_c)  # 与R_nc相对应的最近斜距，记为R0
Nr = Tr * Fr  # 线性调频信号采样点数
BW_range = Kr * Tr  # 距离向带宽
lamda = c / f0  # 波长
fnc = 2 * Vr * np.sin(sita_r_c) / lamda  # 多普勒中心频率，根据公式（4.33）计算。
La_real = 0.886 * 2 * Vr * np.cos(sita_r_c) / BW_dop  # 方位向天线长度，根据公式（4.36）
beta_bw = 0.886 * lamda / La_real  # 雷达3dB波束
La = beta_bw * R0  # 合成孔径长度
a_sr = Fr / BW_range  # 距离向过采样因子
a_sa = Fa / BW_dop  # 方位向过采样因子

Mamb = round(fnc / Fa)  # 多普勒模糊

NFFT_r = Nrg  # 距离向FFT长度
NFFT_a = Naz  # 方位向FFT长度

## 生成单个点目标信号
# 目标位置坐标
delta_R0 = 0  # 将目标1的波束中心穿越时刻，定义为方位向时间零点。
x1 = R0
y1 = delta_R0 + x1 * np.tan(sita_r_c)
nc_1 = (y1 - x1 * np.tan(sita_r_c)) / Vr  # 目标1的波束中心穿越时刻。

s_echo = np.mat(np.zeros((Naz, Nrg)))  # 用来存放生成的回波数据
A0 = 1  # 目标回波幅度

######################           生成轴
tr = np.array((2 * x1 / c + np.arange(-Nrg / 2, (Nrg / 2), 1) / Fr), ndmin=2)  # 距离时间轴
fr = np.array((np.arange(-NFFT_r / 2, NFFT_r / 2) * (Fr / NFFT_r)), ndmin=2)  # 距离频率轴
ta = np.array((np.arange(-Naz / 2, Naz / 2) / Fa), ndmin=2)  # 方位时间轴
fa = np.array((np.arange(-NFFT_a / 2, NFFT_a / 2) * (Fa / NFFT_a) + fnc), ndmin=2)  # 方位频率轴
tr_mtx = np.ones((Naz, 1)) * tr  # 距离时间轴矩阵，大小：Naz*Nrg
ta_mtx = ta.T * np.ones((1, Nrg))  # 方位时间轴矩阵，大小：Naz*Nrg

######################           生成目标回波数据
R_n = np.sqrt(np.power(x1 * np.ones((Naz, Nrg)), 2) + np.power((Vr * ta_mtx - y1 * np.ones((Naz, Nrg))), 2))  # 目标的瞬时斜距
w_range = ((np.abs(tr_mtx - 2 * R_n / c)) <= ((Tr / 2) * np.ones((Naz, Nrg))))
w_azimuth = (np.abs(ta - nc_1) <= (La / 2) / Vr)
w_azimuth = w_azimuth.T * np.ones((1, Nrg))
s_echo = A0 * w_range * w_azimuth * np.exp(-(1j * 4 * np.pi * f0) * R_n / c) * np.exp(
    (1j * np.pi * Kr) * np.power((tr_mtx - 2 * R_n / c), 2))

# plt.pcolor(s_echo.real, cmap='jet')
# plt.colorbar()
# pylab.title('s_echo.real')
# plt.show()
#
# plt.pcolor(s_echo.imag, cmap='jet')
# plt.colorbar()
# pylab.title('s_echo.imag')
# plt.show()
#
# plt.pcolor(np.abs(s_echo), cmap='jet')
# plt.colorbar()
# pylab.title('s_echo.abs')
# plt.show()

########## 利用回波数据成像
S_range = np.fft.fft(s_echo, NFFT_r)

# plt.pcolor(S_range.real, cmap='jet')
# plt.colorbar()
# pylab.title('S_range.real')
# plt.show()
#
# plt.pcolor(abs(S_range), cmap='jet')
# plt.colorbar()
# pylab.title('S_range.abs')
# plt.show()

t_ref = np.mat(np.arange(-Nr / 2, Nr / 2, 1) / Fr)  # 用来生成距离MF的距离时间轴
t_ref_mtx = np.dot(np.ones((Naz, 1)), t_ref)  # 矩阵形式
w_ref = np.mat(np.kaiser(Nr, 2.5))  # 距离向，构建Kaiser窗，此为列向量。
w_ref = np.dot(np.mat(np.ones((Naz, 1))), w_ref)  # 构成矩阵形式，每一行都相同的加窗。
s_ref = np.exp((1j * np.pi * Kr) * (np.power(t_ref_mtx, 2)))
# s_ref = np.pad(s_ref, (0, Nrg-int(Nr)), 'constant')  # 对复制脉冲，后端补零。
S_ref = np.fft.fft(s_ref, NFFT_r)
H_range = np.conj(S_ref)  # 距离向匹配滤波器，零频在两端。
S_range_c = S_range * H_range  # 乘以匹配滤波器，零频在两端。


s_rc = np.fft.ifft(S_range_c)  # 完成距离压缩，回到二维时域。

# plt.pcolor(s_rc.real, cmap='jet')
# plt.colorbar()
# pylab.title('s_rc.real')
# plt.show()
#
# plt.pcolor(abs(s_rc), cmap='jet')
# plt.colorbar()
# pylab.title('s_rc.abs')
# plt.show()

#####  处理脉压的弃置区：弃置长度 = N-1
N_rg = int(Nrg - (Nr - 1))  # 保留长度（完全卷积的长度）
s_rc_c = np.zeros((Naz, N_rg))  # 用来存放去除弃置区后的数据
s_rc_c = s_rc[:, 0:N_rg]  # 取前 N_rg列。

# plt.pcolor(S_range_c.real, cmap='jet')
# plt.colorbar()
# pylab.title('S_range_c.real')
# plt.show()
#
# plt.pcolor(abs(S_range_c), cmap='jet')
# plt.colorbar()
# pylab.title('S_range_c.abs')
# plt.show()
#
#


# 截取后的 ##
# plt.pcolor(s_rc_c.real, cmap='jet')
# plt.colorbar()
# pylab.title('s_rc_c.real')
# plt.show()
#
# plt.pcolor(abs(s_rc_c), cmap='jet')
# plt.colorbar()
# pylab.title('s_rc_c.abs')
# plt.show()


#############  变换到距离多普勒域，进行距离徙动校正 #############
s_rc_c = s_rc_c * np.exp(-1j * 2 * np.pi * fnc * (ta.T * np.ones((1, N_rg))))  # 数据搬移
S_rd = np.fft.fft(s_rc_c, NFFT_a ,0)  # 方位向傅里叶变换，到距离多普勒域

# plt.pcolor(S_rd.real, cmap='jet')
# plt.colorbar()
# pylab.title('S_rd.real')
# plt.show()
#
# plt.pcolor(abs(S_rd), cmap='jet')
# plt.colorbar()
# pylab.title('S_rd.abs')
# plt.show()

# ====================================================================
# 设置方位频率轴——关键点！！！
fa =np.array(fnc + np.fft.fftshift(np.arange(-NFFT_a/2, NFFT_a/2, 1))/NFFT_a*Fa, ndmin=2)      # 方位频率轴如此设置。
# =====================================================================

#  下面这个是改进的，每一个最近斜距（R0）都随着距离门的不同而改变。
tr_RCMC =np.array(2*x1/c + np.arange(-N_rg/2, (N_rg/2), 1)/Fr, ndmin=2)      # 在新的距离线长度下的时间轴
R0_RCMC = (c/2)*tr_RCMC       # 随距离线变化的R0，记为R0_RCMC，用来计算RCM和Ka。

delta_Rrd_fn = np.dot(lamda*lamda*np.power(fa.T, 2),R0_RCMC/(8*Vr*Vr))      # 《合成孔径雷达成像算法与实现》P-146 6.11

num_range = c/(2*Fr)        # 一个距离采样单元，对应的长
delta_Rrd_fn_num = delta_Rrd_fn/num_range      # 每一个方位向频率，其RCM对应的距离采样单元数

R = 8      # sinc插值核长度
S_rd_rcmc = np.zeros((NFFT_a, N_rg), dtype=complex)         # 用来存放RCMC后的值

for p in range(0, NFFT_a):
    for q in range(0, N_rg):
        delta_Rrd_fn_p = delta_Rrd_fn_num[p, q]
        Rrd_fn_p = q + delta_Rrd_fn_p
        Rrd_fn_p_zheng = np.ceil(Rrd_fn_p)     # ceil，向上取整。
        ii = np.array(np.arange(Rrd_fn_p - (Rrd_fn_p_zheng - R / 2), Rrd_fn_p-(Rrd_fn_p_zheng+R / 2), -1), ndmin=2)
        rcmc_sinc = np.sinc(ii)
        # rcmc_sinc = rcmc_sinc / np.sum(rcmc_sinc)   # 插值核的归一化  python 中自动归一化了
        # ii是sinc插值过程的变量;
        # g(x) = sum(h(ii) * g_d(x - ii)) = sum(h(ii) * g_d(ll));
        # 由于S_rd只有整数点取值，且范围有限。因此插值中要考虑它的取值溢出边界问题。
        # 这里我采取循环移位的思想，用来解决取值溢出问题。
        if (Rrd_fn_p_zheng-R/2) > N_rg:
            ll = np.array(np.arange(Rrd_fn_p_zheng - R / 2 - N_rg, Rrd_fn_p_zheng+R / 2-N_rg, 1), ndmin=2)
        else:
            if (Rrd_fn_p_zheng+R/2-1) > N_rg:       # 部分右溢
                ll_1 = np.array(np.arange(Rrd_fn_p_zheng - R / 2, N_rg+1, 1), ndmin=2)
                ll_2 = np.array(np.arange(1, Rrd_fn_p_zheng+R / 2-1-N_rg+1, 1), ndmin=2)
                ll = np.array(np.append(ll_1, ll_2), ndmin=2, dtype=int)
            else:
                if (Rrd_fn_p_zheng+R/2-1) < 1:      # 全左溢（不可能发生，但还是要考虑）
                    ll = np.array(np.arange(Rrd_fn_p_zheng - R / 2 + N_rg, Rrd_fn_p_zheng+R / 2-1+N_rg, 1), ndmin=2, dtype=int)
                else:
                    if (Rrd_fn_p_zheng-R/2) < 1:    # 部分左溢
                        ll_1 = np.array(np.arange(Rrd_fn_p_zheng-R/2+N_rg, N_rg+1, 1), ndmin=2)
                        ll_2 = np.array(np.arange(1, Rrd_fn_p_zheng+R/2, 1), ndmin=2)
                        ll = np.array(np.append(ll_1, ll_2), ndmin=2, dtype=int)
                    else:
                        ll = np.array(np.arange(Rrd_fn_p_zheng - R / 2, Rrd_fn_p_zheng+R / 2, 1), ndmin=2, dtype=int)
        rcmc_S_rd = S_rd[[p], ll-1]
        S_rd_mid= rcmc_sinc*rcmc_S_rd
        S_rd_rcmc[p, q] = np.sum(S_rd_mid)

# plt.pcolor(S_rd_rcmc.real, cmap='jet')
# plt.colorbar()
# pylab.title('S_rd_rcmc.real')
# plt.show()
#
# plt.pcolor(abs(S_rd_rcmc), cmap='jet')
# plt.colorbar()
# pylab.title('S_rd_rcmc.abs')
# plt.show()
# ======= 方位压缩
fa_azimuth_MF = fa      # 方位频率轴，采用和RCMC中所用的频率轴相同。
Ka = 2*Vr*Vr*np.power(np.cos(sita_r_c), 3)/(lamda* R0_RCMC)         # 方位向调频率，是随最近斜距R0变化的。
Ka_1 = 1/Ka                                       # 为了方便计算，先取倒数。
Haz = np.exp(-1j*np.pi*(np.power(fa_azimuth_MF.T, 2)*Ka_1))	    # 方位向匹配滤波器
S_rd_c = S_rd_rcmc*Haz      # 乘以匹配滤波器
s_ac = np.fft.ifft(S_rd_c, NFFT_a, 0)

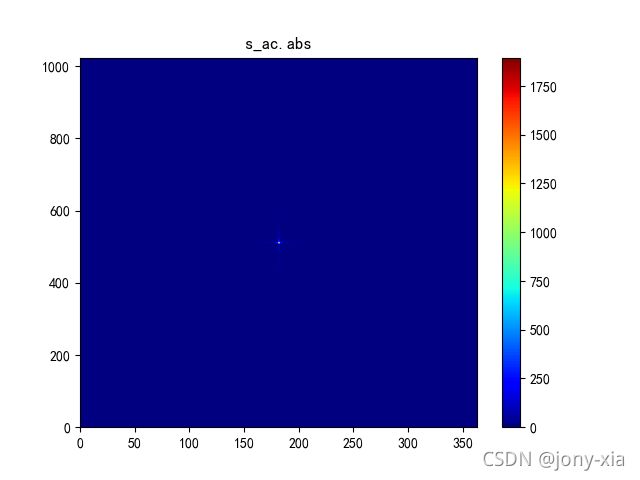
plt.pcolor(abs(s_ac), cmap='jet')
plt.colorbar()
pylab.title('s_ac.abs')
plt.show()