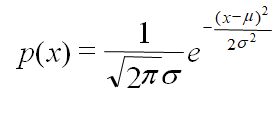数学建模-数据分析

数据的统计描述和分析

统计的基本概念

统计量

1. 表示位置的统计量—平均值和中位数：
   平均值（或均值，数学期望）：X = 1/n ∑X_i
   中位数：将数据由小到大排序后位于中间位置的那个数值。

2. 表示变异程度的统计量—标准差、方差和极差：
   标准差：s = [ 1/ (n-1) ∑ ( X_i - X )² ]^1/2
   它是各个数据与均值偏离程度的度量。
   方差：标准差的平方。
   极差：样本中最大值与最小值之差。

3. 表示分布形状的统计量—偏度和峰度：
   偏度：g₁ = (1/ s³ )∑( X_i - X )³
   峰度：g₂ = (1/ s⁴ )∑( X_i - X )⁴
   偏度反映分布的对称性，g₁ >0称为右偏态，此时数据位于均值右边的比位于左边的多；g₁ <0称为左偏态，情况相反；而 g₁ 接近0则可认为分布是对称的。
   峰度是分布形状的另一种度量，正态分布的峰度为3，若 g₂ 比 3 大很多，表示分布有沉重的尾巴，说明样本中含有较多远离均值的数据，因而峰度可用作衡量偏离正态分布的尺度之一。

分布函数的近似求法

1. 整理资料： 把样本值x₁，x₂，…，x_n进行分组，先将它们依大小次序排列，得x₁^*＜x₂^*＜…＜x_n^*，在包含 [x₁^*, x_n^*] 的区间 [a，b] 内插入一些等分点：注意要使每一个区间 （i=1，2，…，n-1）内都有样本观测值xi（i=1，2，…，n-1）落入其中。

2. 求出各组的频数和频率：统计出样本观测值在每个区间 [x_i^*, x_i+1^*] 中出现的次数 ，它就是这区间或这组的频数。计算频率 f_i = n_i/n。

3. 作频率直方图：在直角坐标系的横轴上，标出 x₁，x₂，…，x_n 各点，分别以 [x_i^*, x_i+1^*] 为底边，作高为 f_i/dx_i^* 的矩形， 即得频率直方图。

几个在统计中常用的概率分布

1. 正态分布 N ( μ , σ² )
   密度函数：
   
   分布函数：
   
   其中 μ 为均值，σ² 为方差。

标准正态分布中 μ = 0，σ² = 1。

正态分布图像：

2. χ² 分布 χ² (n)
   若随机变量 X₁，X₂，… X_n 相互独立，都服从标准正态分布 N ( 0 , 1 )，则随机变量 Y = X₁ + X₂ +… + X_n 服从自由度为n的 分布，记为Y~ (n) 。Y的均值为 n ，方差为 2n 。

χ² 分布图像：

3. t 分布 t (n)
   若X ~ N ( 0 , 1) ，Y~ ( n )，且相互独立，则随机变量 T = X / √ (Y / N ) 服从自由度为n的t分布，记为T~ t ( n )。 t 分布 t ( 20 ) 的密度函数曲线和 N ( 0 , 1) 的曲线形状相似。理论上 n → ∞ 时，T~ t ( n ) → N ( 0 , 1)。

t 分布图像：

4. F 分布 F ( n₁ , n₂ )

若 X ~ χ² ( n₁ )，Y ~ χ² ( n₂ )，且相互独立，则随机变量 F = ( X * n₂ ) / ( Y * n₁ ) 服从自由度为 ( n₁，n₂ ) 的 F 分布，记作 F ~ F ( n₁，n₂ )。由 F 分布的定义可以得到 F 分布的一个重要性质： 若 F ~ F ( n₁，n₂ )，则 1 / F ~ F ( n₂，n₁ )。

F 分布图像：

参数估计

无论总体X的分布函数 F ( x ; θ₁ , θ₂ ,…, θ_k ,）的类型已知或未知，我们总是需要去估计某些未知参数或数字特征，这就是参数估计问题。即参数估计就是从样本 ( x₁，x₂，…，x_n ) 出发，构造一些统计量 θ_i^* ( x₁，x₂，…，x_n ) ( i = 1, 2 ,…, k ) 去估计总体X中的某些参数(或数字特征) θ_i ( i = 1, 2 ,…, k ) 。这样的统计量称为估计量。

1. 点估计：构造 θ_i 的函数 θ_i^* ( x₁，x₂，…，x_n ) 作为参数 θ_i 的点估计量，称统计量 θ_i^* 为总体X参数 θ_i 的点估计量。

2. 区间估计：构造两个函数 θ_i1 ( x₁，x₂，…，x_n ) 和 θ_i2 ( x₁，x₂，…，x_n ) 做成区间，把这 ( θ_i1 , θ_i2 ) 作为参数 的区间估计。

假设检验

对总体X的分布律或分布参数作某种假设，根据抽取的样本观察值，运用数理统计的分析方法，检验这种假设是否正确，从而决定接受假设或拒绝假设。

1. 参数检验：如果观测的分布函数类型已知，这时构造出的统计量依赖于总体的分布函数，这种检验称为参数检验。
   参数检验的目的往往是对总体的参数及其有关性质作出明确的判断。

2. 非参数检验：如果所检验的假设并非是对某个参数作出明确的判断，因而必须要求构造出的检验统计量的分布函数不依赖于观测值的分布函数类型，这种检验叫非参数检验。如要求判断总体分布类型的检验就是非参数检验。

假设检验的一般步骤

1. 根据实际问题提出原假设 H₀ 与备择假设 H₁，即说明需要检验的假设的具体内容；
2. 选择适当的统计量，并在原假设 H₀ 成立的条件下确定该统计量的分布；
3. 按问题的具体要求，选取适当的显著性水平 α ，并根据统计量 的分布查表，确定对应于 α 的临界值。一般 α 取0.05 , 0.01 或 0.10 。
4. 根据样本观测值计算统计量的观测值，并与临界值进行比较，从而在检验水平 条件下对拒绝或接受原假设 H₀ 作出判断。

MATLAB统计工具箱的使用

数据的录入、保存和调用

1. 用产生向量的方法输入数据 x , y 等

2. 将变量x，y的数据保存在文件data中save data x y

3. 进行统计分析时，调用数据文件data中的数据load data

基本统计量

对随机变量x，计算其基本统计量的命令如下：

mean(x)              %均值
median(x)            %中位数
std(x)               %标准差
var(x)               %方差
skewness(x)          %偏度
kurtosis(x)          %峰度

常见概率分布的函数

常见的几种分布的命令字符为：

exp          %指数分布     
poiss        %帕松分布
beta         %分布  
weib         %威布尔分布
chi2         %分布
t            %t分布
F            %F分布

MATLAB工具箱对每一种分布都提供五类函数，其命令字符为：
概率密度：pdf
概率分布：cdf
逆概率分布：inv
均值与方差：stat
随机数生成：rnd
当需要一种分布的某一类函数时，将以上所列的分布命令字符与函数命令字符接起来，并输入自变量（可以是标量、数组或矩阵）和参数即可。

频数直方图的描绘

1. 给出数组data的频数表的命令为：
   [N , X] = hist (data , k)
   此命令将区间 [ min (data) , max (data) ]分为k个小区间（缺省为10），返回数组data落在每一个小区间的频数N和每一个小区间的中点X。

2. 描绘数组data的频数直方图的命令为：
   hist(data,k)

参数估计

正态总体的参数估计

设总体服从正态分布，则其点估计和区间估计可同时由以下命令获得：
[ muhat,sigmahat,muci,sigmaci ] = normfit (X,alpha)

此命令在显著性水平alpha下估计数据X的参数（alpha缺省时设定为0.05），返回值muhat是X的均值的点估计值，sigmahat 是标准差的点估计值，muci 是均值的区间估计，sigmaci 是标准差的区间估计。

其它分布的参数估计

1. 取容量充分大的样本（n>50），按中心极限定理，它近似地服从正态分布；

2. 使用Matlab工具箱中具有特定分布总体的估计命令：

[ muhat, muci ] = expfit (X,alpha)     %在显著性水平alpha下，求指数分布的数据X的均值的点估计及其区间估计.

[ lambdahat, lambdaci ] = poissfit (X,alpha)     %在显著性水平alpha下，求泊松分布的数据X 的参数的点估计及其区间估计.

[ phat, pci ] = weibfit (X,alpha)      %在显著性水平alpha下，求Weibull分布的数据X 的参数的点估计及其区间估计.

假设检验

总体服从正态分布的情况下，可用以下命令进行假设检验：

1. 总体方差sigma2已知时，总体均值的检验使用 z-检验：

[ h,sig,ci ] = ztest (x, m, sigma, alpha, tail)

检验数据 x 的关于均值的某一假设是否成立，其中sigma 为已知方差， alpha 为显著性水平，究竟检验什么假设取决于 tail 的取值：
“ tail = 0，检验假设“x 的均值等于 m ”
“ tail = 1，检验假设“x 的均值大于 m ”
“ tail = -1，检验假设“x 的均值小于 m ”
tail的缺省值为 0， alpha的缺省值为 0.05。
返回值 h 为一个布尔值，h=1 表示可以拒绝假设，h=0 表示不可以拒绝假设，sig 为假设成立的概率，ci 为均值的 1-alpha 置信区间。

2. 总体方差sigma2未知时，总体均值的检验使用t-检验：

[ h,sig,ci ] = ttest (x, m, alpha, tail)

检验数据 x 的关于均值的某一假设是否成立，其中alpha 为显著性水平，究竟检验什么假设取决于 tail 的取值：
“ tail = 0，检验假设“x 的均值等于 m ”
“ tail = 1，检验假设“x 的均值大于 m ”
“ tail = -1，检验假设“x 的均值小于 m ”
tail的缺省值为 0， alpha的缺省值为 0.05。
返回值 h 为一个布尔值，h=1 表示可以拒绝假设，h=0 表示不可以拒绝假设，sig 为假设成立的概率，ci 为均值的 1-alpha 置信区间。

3. 两总体均值的假设检验使用 t-检验：

[ h,sig,ci ] = ttest2 (x, y, alpha, tail)

检验数据 x ，y 的关于均值的某一假设是否成立，其中alpha 为显著性水平，究竟检验什么假设取决于 tail 的取值：
tail = 0，“检验假设“x 的均值等于 y 的均值 ”
tail = 1，“检验假设“x 的均值大于 y 的均值 ”
tail =-1，“检验假设“x 的均值小于 y 的均值 ”
tail的缺省值为 0， alpha的缺省值为 0.05。
返回值 h 为一个布尔值，h = 1 表示可以拒绝假设，h = 0 表示不可以拒绝假设，sig 为假设成立的概率，ci 为与 x 与 y 均值差的 1-alpha 置信区间。

4. 非参数检验：总体分布的检验

Matlab工具箱提供了两个对总体分布进行检验的命令:

h = normplot (x)

此命令显示数据矩阵x的正态概率图.如果数据来自于正态分布，则图形显示出直线性形态.而其它概率分布函数显示出曲线形态.

h = weibplot (x)

此命令显示数据矩阵x的Weibull概率图.如果数据来自于Weibull分布，则图形将显示出直线性形态.而其它概率分布函数将显示出曲线形态.