数学建模常用的数据处理方法及例子汇总（持续更新中）

常用的数据处理方法：

一、人口模型和数据拟合

1.1 指数型人数模型

马尔萨斯模型

设时刻t时人口为$x(t)$，单位时间内的人口增长率为r，则$\Delta t$时间内增长的人口为：
$$x(t+\Delta t)-x(t)=x(t)\times r\times \Delta t$$
当$\Delta t\to 0$，得到微分方程：
$$\frac{dx}{dt}=rx,x(0)=x_0$$
则：$x(t)=x_0{e}^{rt}$

代求参数 $x_0,r$

为了便于求解，两边取对数有：$y=a+rt$，其中$y=\ln x,a=\ln x_0$，该模型化即为线性求解

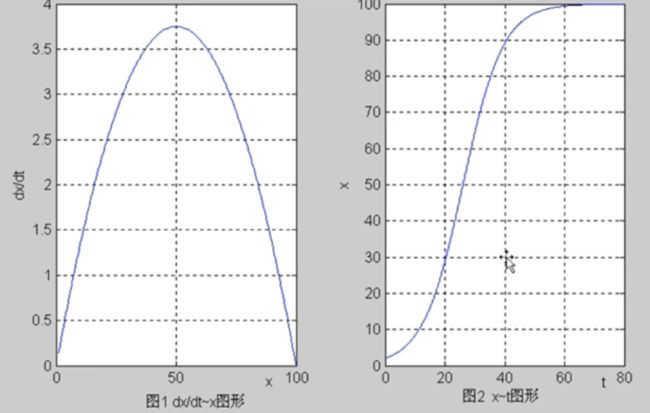
1.2 阻滞型人口模型

s型曲线

信息的传播，汽车数量的增长速度

用的时候就把模型简单介绍，然后把数据代入画图就行了

设时刻t时人口为$x(t)$，环境允许的最大人口数量为$x_m$，人口净增长率岁人口数量的增加而线性减少，即
$$r(t)=r(1-\frac{x}{x_m})$$
由此建立阻滞型人口微分方程：

咋积分的？？

$$\frac{dx}{dt}=r(1-\frac{x}{x_m})x,x(0)=x_0$$

则：
$$x(t)=\frac{x_m}{1+(\frac{x_m}{x_0}-1)e^{-rt}}$$
带求参数：$x_0,x_m,r$。此即Logistic函数

当$x=\frac{x_m}{2}$时，x增长最快，即$\frac{dx}{dt}$最大

实例1：美国人口数据处理

38：23左右开始讲

太拉了，整个就念代码

regress：线性回归函数

nlintfit：非线性拟和函数

​ $beta:[x_0,r,x_m]$

​ $beta0$是需要给的初始值，给个大概范围就可以

其中logisfun是自己编写的函数

二、神经网络方法

1. 多层向前神经网络原理介绍

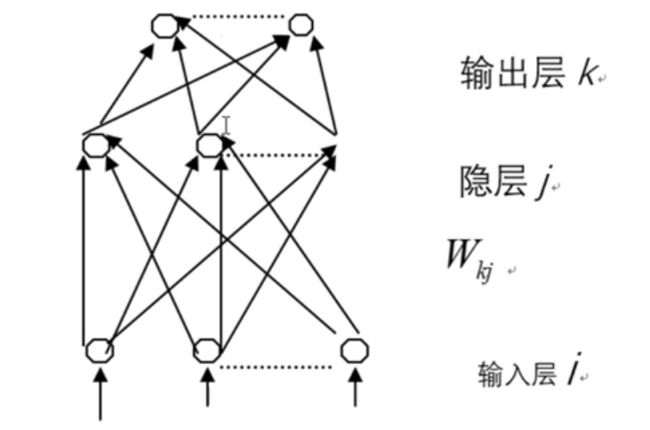
多层前向神经网络(MLP)是神经网络中的一种，它由一些最基本的神经元即节点组成，下图就是这样一个网络。这种网络的结构如下：网络由分为不同层次的节点集合组成，每一层的节点输出到下一层节点，这些输出值由于连接不同而被放大、衰减或抑制。除了输入层外，每一节点的输入为前-一层所有节点输出值的和。每- - 节点的激励输出值由节点输入、激励函数及偏置量决定。
下图中，输入模式的各分量作为第i层各节点的输入，这一节点的输出，或者完全等于它们的输入值，或由该层进行归一化处理，使该层的输出值都在+1或-1之间。

在第j层，节点的输入值为：
$$ne{t}_i=\sum w_{ji}{o}_i+{\theta }_j$$
式中的${\theta }_j$为阈值，正阈值的作用将激励函数沿x轴向左平移，节点的输出值为：
$$o_j=f(ne{t}_j)$$
事中f为节点的激励函数，通常选择如下Sigmoid函数：
$$f(x)=\frac{1}{1+exp(-x)}$$
在第k层的网络节点的输入为：
$$ne{t}_k=\sum w_{kj}{o}_j+{\theta }_k$$
而输出为：
$$o_k=f(ne{t}_k)$$
在网络学习阶段，网络输入为模式样本$x_p=x_{pi}$，网络要修正自己的权值及各节点的阀值，使网络输出不断接近期望值$t_{pk}$，每做一次调整后，换一对输入与期望输出，再做一次调整，直到满足所有样本的输入与输出间的对应。一般说来，系统输出值$o_{pk}$与期望输出值$t_{pk}$是不相等的。对每一个输入的模式样本，平方误差$E_p$为:
$$E_p=\frac{1}{2}\sum _k(t_{pk}-o_{pk}{)}^2$$
而对于全部学习样本，系统的总误差为：
$$E_p=\frac{1}{2p}\sum _p\sum _k(t_{pk}-o_{pk}{)}^2$$
在学习过程中，系统将调整链接权和阈值，使得$E_p$尽可能快地下降

2. Matlab相关函数介绍

（1）网络初始化函数

$$net=newff([x_m,x_M],[h_1,h_2,...,h_k],\{f_1,f_2,...,f_k\})$$
其中，$x_m$ 和$x_M$分别为列向量，存储各个样本输入数据的最小值和最大值（即各个特征的最小值和最大值）；第二个输入变量是一个行向量，输入各层节点数（从隐层开始）；第三个输入变量是字符串，代表该层的传输函数（从隐层开始）。

常用tansig和logsig函数。其中

$$\begin{array}{rlr}& tansig(x)=\frac{1-e^{-2x}}{1+e^{-2x}}& 将所有值映射到[-1,+1]\\ & logsig(x)=\frac{1}{1+e^{-x}}& 将所有值映射到[0,+1]\end{array}$$
除了上面方法给网络赋值外，还可以用下面格式设定参数。

$Net.trainParam.epochs=1000$ 设置迭代次数

$Net.trainFcn{=}^{\prime }traing{m}^{\prime }$ 设定带动量的梯度下降算法

（2）网络训练函数
$$[net,tr,Y1,E]=train(net,X,Y)$$
其中X为$n\times M$矩阵，n为输入变量的个数，M为样本数，Y为$m\times M$矩阵，m为输出变量的个数。X，Y分别存储样本的输入输出数据。net为返回后的神经网络对象，tr为训练跟踪数据，$tr.pref$为各步目标函数值。Y1位网络的最后输出，E1为训练误差向量

（3）网络泛化函数
$$Y2=sim(net,X1)$$
其中X1位输入数据矩阵，各列为样本数据，Y2位对应输出值

3.神经网络实验

神经网络主要用来函数拟合，插值，目标分类，模式识别

（1）函数仿真实验

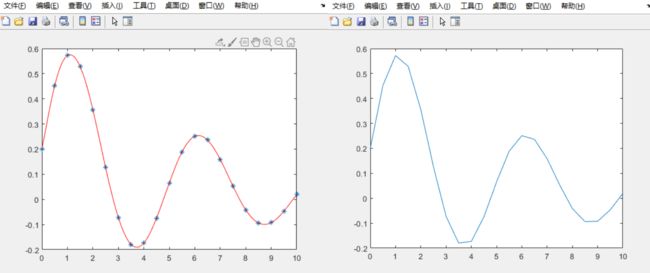
产生下列函数在$[0,10]$区间上间隔0.5的数据，然后用神经网络进行学习，并推广到$[0.10]$上间隔为0.1上各店的函数值。并分别做出图形
$$y=0.2e^{-0.2x}+0.5\times e^{-0.15x}.sin(1.25x)0\le x\le 10$$
Matlab程序：

x=0:0.5:10;
y=0.2*exp(-0.2*x)+0.5*exp(-0.15*x).*sin(1.25*x);
plot(x,y); %画出原始图

net.trainParam.epochs=5000; % 设定迭代次数
net=newff([0,10],[6,1],{'tansig','tansig'}); %初始化网络
net=train(net,x,y); %进行网络训练

x1=0:0.1:10;
y1=sim(net,x1); %数据泛化
plot(x,y,'*',x1,y1,'r');

（2）目标分类

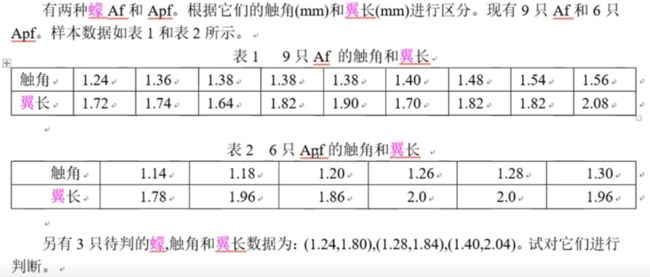
MCM89A蠓的分类

这里，我们可用三层神经网络进行判别。

输入为15个二维向量，输出也为15个二维向量。其中Af对一个的目标向两位（1,0），Apf对应的目标向量为（0,1）

Matlab程序：

x=[1.24,1.36,1.38,1.38,1.38,1.40,1.48,1.54,1.56,1.13,1.18,1.20,1.26,1.28,1.30;
    1.72,1.74,1.64,1.82,1.90,1.70,1.82,1.82,2.08,1.78,1.96,1.86,2.0,2.0,1.96];
y=[1,1,1,1,1,1,1,1,1,0,0,0,0,0,0;
    0,0,0,0,0,0,0,0,0,1,1,1,1,1,1];

net.trainParam.epochs=2500; %设定迭代次数
XM=minmax(x); %求最小值与最大值
net=newff(XM,[5,2],{'logsig','logsig'}); %初始化网络
net=train(net,x,y); %进行网络训练
x1=[1.24,1.28,1.40;
    1.80,1.84,2.04]; %待分类样本
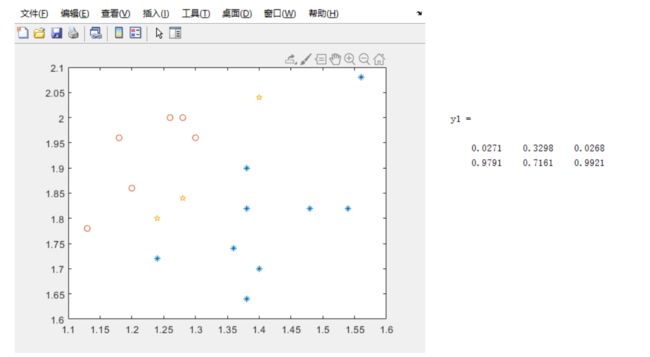
y1=sim(net,x1) %数据泛化
plot(x(1,1:9),x(2,1:9),'*',x(1,10:15),x(2,10:15),'o',x1(1,:),x1(2,:),'p') %画原始数据图

注意，在这里每次运行结果都可能不一样，也就是说每一只可能在两次运行中被分到的类中都不一样

以两个分量越靠近就判断为哪一类。 从该结果看，三个样本都为Apf。但由于每次训练初始参数的随机性，而待判的3个样本在两类的临界区，导致不同的训练结果会有差异，这也正常。

三、灰色模型及预测

灰色系统理论建模要求原始数据必须等时间间距。首先对原始数据进行累加生成，目的是弱化原始时间序列数据的随机因素，然后建立生成数的微分方程。GM(1.1)模型是灰色系统理论中的单序列一阶灰色微分方程，它所需信息较少，方法简便。

设一直序列为$x^{(0)}(1),x^{(0)}(2),...,x^{(0)}(n)$，做一个累加AGO（Acumulated Generating Operation）生成新序列：
$$x^{(1)}(1),x^{(1)}(2),...x^{(1)}(n)$$
其中
$$x^{(1)}(1)=x^{(0)}(1),x^{(1)}(2)=x^{(0)}(1)+x^{(0)}(2),...$$
即
$$x^{(1)}(k)=\sum _{i=1}^k{x}^{(0)}(i)k=1,2,...,n$$
生成均值序列（均值是为了解决毛刺）：
$$z^{(1)}(k)=\alpha x^{(1)}(k)+(1-\alpha )x^{(1)}(k-1)k=2,3,...,n\text{\hspace{1em}(1)}$$
其中$0\le \alpha \le 1$。通常可取$\alpha =0.5$，建立灰微分方程（离散微分方程）：

假设符合这样的规律，然后再去验证

$$x^{(0)}(k)+a{x}^{(1)}(k)=bk=2,3,...,n\text{\hspace{1em}(2)}$$

响应的GM(1.1)白化微分方程（连续微分方程）为：
$$\frac{d{x}^{(1)}}{dt}+a{x}^{(1)}(t)=b\text{\hspace{1em}(3)}$$
将方程（2）变形为：
$$-a{z}^{(1)}(k)+b=x^{(0)}(k)\text{\hspace{1em}(4)}$$
其中a，b为待定模型参数

将方程组（4）采用矩阵形式表达为：

即：
$$X\beta =Y\text{\hspace{1em}(6)}$$
解方程（6）的到最小二乘解为（可以求出来a，b）：
$$\hat{\beta }=(a,b{)}^T=(X^{T}X{)}^{-1}{X}^{T}Y\text{\hspace{1em}(7)}$$
求解微分方程（3）得到GM（1,1）模型的离散解：
$${\hat{x}}^{(1)}(k)=[x^{(0)}(1)-\frac{b}{a}]e^{-\alpha (k-1)}+\frac{b}{a}k=2,3,...,n\text{\hspace{1em}(8)}$$
还原为原始数列，预测模型为：
$${\hat{x}}^{(0)}(k)={\hat{x}}^{(1)}(k)-{\hat{x}}^{(1)}(k-1)k=2,3,...,n\text{\hspace{1em}(9)}$$
将式（8）代入式（9）得
$${\hat{x}}^{(0)}(k)=[x^{(0)}(1)-\frac{b}{a}]e^{-a(k-1)}(1-e^a)k=2,3,...,n\text{\hspace{1em}(10)}$$
GM(1.1)模型与统计模型相比，具有两个显著优点：一是灰色模型即使在少量数据情况下建立的模型，精度也会很高，而统计模型在少量数据情况下，精度会相对差一些；二是灰色模型从其机理上讲，越靠近当前时间点精度会越高，因此灰色模型的预测功能优于统计模型。灰色系统建模实际上是一种以数找数的方法，从系统的一个或几个离散数列中找出系统的变化关系，试图建立系统的连续变化模型。

例子

2003年的SARS疫情对中国部分行业的经济发展产生了一定的影响，特别是对部分疫情严重的省市的相关行业所造成的影响是明显的。经济影响分为直接经济影响和间接影响。很多方面难以进行定量评估。现就某市SARS疫情对商品零售业的影响进行定量的评估分析。

解答：

SARS发生在2003年4月。因此我们可根据1997年到2002年的数据，预测2003年的各月的零售额，并与实际的零售额进行。从而判断2003年倒底哪几个月受到SARS影响，并给出影响大小的评估。

将1997–2002年的数据记作矩阵$A_{6\times 12}$，代表6年的72个数据

计算各年平均值
$$x^{(0)}(i)=\frac{1}{12}\sum _{j=1}^{12}{a}_{ij}i=1,2,...,6$$
得到
$$x^{(0)}=(87.6167,98.5000,108,4750,118.4167,132.8083,145.4083)$$
计算累加序列
$$x^{(1)}(k)=\sum _{i=1}^k{x}^{(0)}(i)k=1,2...,6$$
得到
$$x^{(1)}=(87.6167,186.1167,294.5917,413.0083,545.8167.691.2250)$$
生成均值序列：