2021年五一杯C题-数据驱动的异常检测与预警问题

2021年五一杯数学建模

C题 数据驱动的异常检测与预警问题

原题再现：

  推动生产企业高质量发展，最根本的底线是保证安全、防范风险，而生产过程中产生的数据能够实时反映潜在的风险。附件1为某生产企业某日00:00:00-22:59:59由生产区域的仪器设备记录的时间序列数据（已经进行数据脱敏），本题未给出数据的具体名称，这些数据可能是温度、浓度、压力等与安全密切相关的数据。
  请依据附件1数据，建立数学模型，完成以下问题：

  问题1：附件1所给出的数据都可能存在波动，且所有波动都在安全值范围内。有些波动可能是正常性波动，例如随着外界温度或者产量变化的波动，或者可能是传感器误报，这些波动具有规律性、独立性、偶发性等特点，并不能产生安全风险，我们视为非风险性异常，不需要人为干预；有些波动具有持续性、联动性等特点，这些异常性波动的出现是生产过程中的不稳定因素造成的，预示着可能存在安全隐患，我们视为风险性异常，需要人为干预、分析和评定风险等级。请建立数学模型，给出判定非风险性异常数据和风险性异常数据的方法。

  问题2：结合问题1的结果，建立数学模型，给出风险性异常数据异常程度的量化评价方法，要求使用百分制（0-100分）对每个时刻数据异常程度进行评价（分值越高表示异常程度越高）。应用所建立的模型和附件1的数据，找到数据中异常分值最高的5个时刻及这5个时刻对应的异常传感器编号（每个时刻只填写5个异常程度最高的传感器编号，异常传感器不足5个则无需填满；如果得分为0，可以不用填写异常传感器编号），并给出数学模型对所得结果进行评价。

  问题3：为了提前发现未来生产过程中可能存在的风险隐患，请建立风险性异常预警模型，预测当日23:00:00-23:59:59可能产生的风险性异常。结合问题2中给出的风险性异常程度量化评价方法，指出23:00:00-23:59:59中四个时间段（见表2），每个时间段内的最高异常分值及对应的异常传感器编号（只填写5个异常程度最高的传感器编号，异常传感器不足5个则无需填满；如果得分为0，可以不用填写异常传感器编号）。

  问题4：根据问题2和问题3中的结果，建立数学模型对该生产企业整个生产系统的安全性进行评价，请在00:00:00-23:59:59内每隔30分钟，用0-100分进行安全性评分，0分表示安全性最低，100分表示安全性最高（包括00:00:00-23:00:00的得分和23:00:00-23:59:59的预测得分），并用适当的方法对所给评分的结果进行评价和敏感性分析。

整体求解过程概述(摘要)

  针对问题一，考虑到附件的数据庞大，首先对数据进行归一化预处理，然后使用主成分分析法对相似度较高的数组进行降维，得到 36 组具有代表性的传感器数据并进行滤波，以便分析其主要的波动而忽略微小波动。考虑到随外界因素变化而产生的波动为非风险性异常，所以于数据网站上查找24 小时的平均温度、电压数据，将与其相似的数据波动判定为非风险性异常数据。然后使用 ARIMA 时间序列分析对 36 组数据的主要波动进行分析，得到周期性（规律性）和非周期性（无规律性）波动，并分别判定为非风险性异常数据和风险性异常数据，使问题一得到解决。
  针对问题二，结合问题一中已经对异常数据进行了判定，本问对风险性异常数据进行了更细致的划分，使用 NCA 对不同种类的异常数据赋予不同的权值，以实现风险异常程度的量化评价
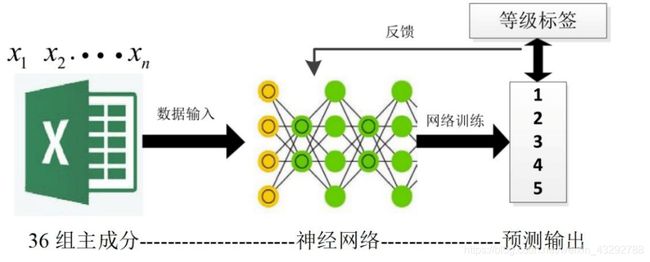
  针对问题三，基于 ARIMA，使用神经网络对 ARIMA 的参数进行优化，以提升模型预测的精度，预测了当日 23:00:00-23:59:59 可能产生的风险性异常，并得到了数据表格。
  针对问题四，将问题二中得到的各时间得分进行积分处理，再转换成百分制，对该生产企业整个生产系统的安全性进行评价，得到了数据表格，并对所给评分的结果进行评价和敏感性分析。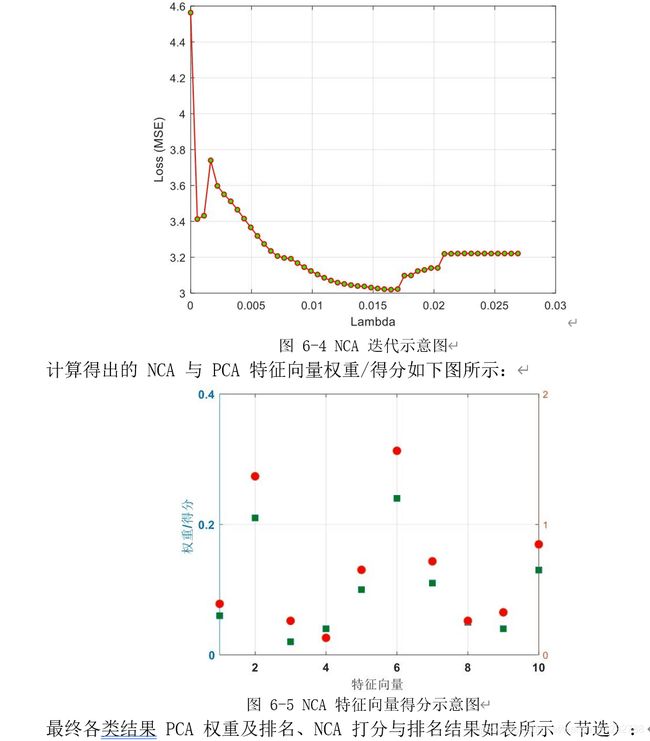

模型假设：

  结合本题的实际情况，为确保模型求解的合理性以及准确性，对所建立的模型排除一些因素的干扰，我们对模型进行假设。
  1、假设不考虑非风险性异常数据与风险性异常数据以外的可能性；
  2、假设忽略所给出的风险性异常数据之外的因素对系统整体的安全性的影响；
  3、假设某企业在这一天的观测数据可代表该企业整个系统的安全性数据；
  4、假设判断出的风险性异常数据不包括非风险性异常数据；

问题分析：

  问题一分析
  针对问题一，考虑到附件的数据庞大，首先对数据进行归一化预处理，然后使用主成分分析法对相似度较高的数组进行降维，得到具有代表性的传感器数据，并进行滤波，以便分析其主要的波动而忽略微小波动。考虑到随外界因素变化而产生的波动为非风险性异常，故于数据网站上查找 24 小时的平均温度、电压数据，将与其相似的数据波动判定为非风险性异常数据。然后使用 ARIMA 时间序列分析对数据的主要波动进行分析，使问题一得到解决。
  问题二分析
  针对问题二，结合问题一中已经对异常数据进行了判定，本问需要对风险性异常数据进行了更细致的划分，使用 NCA 对不同种类的异常数据赋予不同的权值，以实现风险异常程度的量化评价，使问题得到解决。
  问题三分析
  针对问题三，基于 ARIMA，使用神经网络对 ARIMA 的参数进行优化，以提升模型预测的精度，预测了当日 23:00:00-23:59:59 可能产生的风险性异常，并得到了数据表格。
  问题四分析
  针对问题四，将问题二中得到的各时间得分进行积分处理，再转换成百分制，对该生产企业整个生产系统的安全性进行评价，得到了数据表格，并对所给评分的结果进行评价和敏感性分析。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分Python程序如下:

import math
import random
random.seed(0)
def rand(a,b): #随机函数
    return (b-a)*random.random()+a
 
def make_matrix(m,n,fill=0.0):#创建一个指定大小的矩阵
    mat = []
    for i in range(m):
        mat.append([fill]*n)
    return mat
 
#定义sigmoid函数和它的导数

def sigmoid(x):
    return 1.0/(1.0+math.exp(-x))
def sigmoid_derivate(x):
    return x*(1-x) #sigmoid函数的导数
 
class BPNeuralNetwork:
    def __init__(self):#初始化变量
        self.input_n = 0
        self.hidden_n = 0
        self.output_n = 0
        self.input_cells = []
        self.hidden_cells = []
        self.output_cells = []
        self.input_weights = []
        self.output_weights = []
        self.input_correction = []
        self.output_correction = []
    #三个列表维护：输入层，隐含层，输出层神经元
    def setup(self,ni,nh,no):
        self.input_n = ni+1 #输入层+偏置项
        self.hidden_n = nh  #隐含层
        self.output_n = no  #输出层
 
        #初始化神经元
        self.input_cells = [1.0]*self.input_n
        self.hidden_cells= [1.0]*self.hidden_n
        self.output_cells= [1.0]*self.output_n
 
        #初始化连接边的边权
        self.input_weights = make_matrix(self.input_n,self.hidden_n) #邻接矩阵存边权：输入层->隐藏层
        self.output_weights = make_matrix(self.hidden_n,self.output_n) #邻接矩阵存边权：隐藏层->输出层
 
        #随机初始化边权：为了反向传导做准备--->随机初始化的目的是使对称失效
        for i in range(self.input_n):
            for h in range(self.hidden_n):
                self.input_weights[i][h] = rand(-0.2 , 0.2) #由输入层第i个元素到隐藏层第j个元素的边权为随机值
 
        for h in range(self.hidden_n):
            for o in range(self.output_n):
                self.output_weights[h][o] = rand(-2.0, 2.0) #由隐藏层第i个元素到输出层第j个元素的边权为随机值
        #保存校正矩阵，为了以后误差做调整
        self.input_correction = make_matrix(self.input_n , self.hidden_n)
        self.output_correction = make_matrix(self.hidden_n,self.output_n)
 
    #输出预测值
    def predict(self,inputs):
        #对输入层进行操作转化样本
        for i in range(self.input_n-1):
            self.input_cells[i] = inputs[i] #n个样本从0~n-1
        #计算隐藏层的输出，每个节点最终的输出值就是权值*节点值的加权和
        for j in range(self.hidden_n):
            total = 0.0
            for i in range(self.input_n):
                total+=self.input_cells[i]*self.input_weights[i][j]
            # 此处为何是先i再j，以隐含层节点做大循环，输入样本为小循环，是为了每一个隐藏节点计算一个输出值，传输到下一层
            self.hidden_cells[j] = sigmoid(total) #此节点的输出是前一层所有输入点和到该点之间的权值加权和
 
        for k in range(self.output_n):
            total = 0.0
            for j in range(self.hidden_n):
                total+=self.hidden_cells[j]*self.output_weights[j][k]
            self.output_cells[k] = sigmoid(total) #获取输出层每个元素的值
        return self.output_cells[:]  #最后输出层的结果返回
 
    #反向传播算法：调用预测函数，根据反向传播获取权重后前向预测，将结果与实际结果返回比较误差
    def back_propagate(self,case,label,learn,correct):
        #对输入样本做预测
        self.predict(case) #对实例进行预测
        output_deltas = [0.0]*self.output_n #初始化矩阵
        for o in range(self.output_n):
            error = label[o] - self.output_cells[o] #正确结果和预测结果的误差：0,1，-1
            output_deltas[o]= sigmoid_derivate(self.output_cells[o])*error#误差稳定在0~1内
 
        #隐含层误差
        hidden_deltas = [0.0]*self.hidden_n
        for h in range(self.hidden_n):
            error = 0.0
            for o in range(self.output_n):
                error+=output_deltas[o]*self.output_weights[h][o]
            hidden_deltas[h] = sigmoid_derivate(self.hidden_cells[h])*error
        #反向传播算法求W
        #更新隐藏层->输出权重
        for h in range(self.hidden_n):
            for o in range(self.output_n):
                change = output_deltas[o]*self.hidden_cells[h]
                #调整权重：上一层每个节点的权重学习*变化+矫正率
                self.output_weights[h][o] += learn*change + correct*self.output_correction[h][o]
        #更新输入->隐藏层的权重
        for i in range(self.input_n):
            for h in range(self.hidden_n):
                change = hidden_deltas[h]*self.input_cells[i]
                self.input_weights[i][h] += learn*change + correct*self.input_correction[i][h]
                self.input_correction[i][h] =  change
        #获取全局误差
        error = 0.0
        for o in range(len(label)):
            error = 0.5*(label[o]-self.output_cells[o])**2 #平方误差函数
        return error
 
    def train(self,cases,labels,limit=10000,learn=0.05,correct=0.1):
        for i in range(limit): #设置迭代次数
            error = 0.0
            for j in range(len(cases)):#对输入层进行访问
                label = labels[j]
                case = cases[j]
                error+=self.back_propagate(case,label,learn,correct) #样例，标签，学习率，正确阈值
 
    def test(self): #学习异或
        cases = [
            [0, 0],
            [0, 1],
            [1, 0],
            [1, 1],
        ] #测试样例
        labels = [[0], [1], [1], [0]] #标签
        self.setup(2,5,1) #初始化神经网络：输入层，隐藏层，输出层元素个数
        self.train(cases,labels,10000,0.05,0.1) #可以更改
        for case in  cases:
            print(self.predict(case))
 
if __name__ == '__main__':
    nn = BPNeuralNetwork()

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可