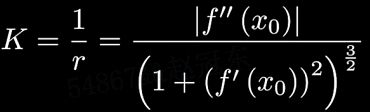曲线曲率介绍和python求法
目录
- 曲率
-
- 1.1 弧长参数 s
- 图解数学
- Python 中的曲线曲率
- 参考资料
曲率
对于圆而言,曲率与半径成反比,是半径的倒数,而直线的曲率为 0。
K = 1 r \pmb{K}=\frac{1}{\pmb{r}} K=r1
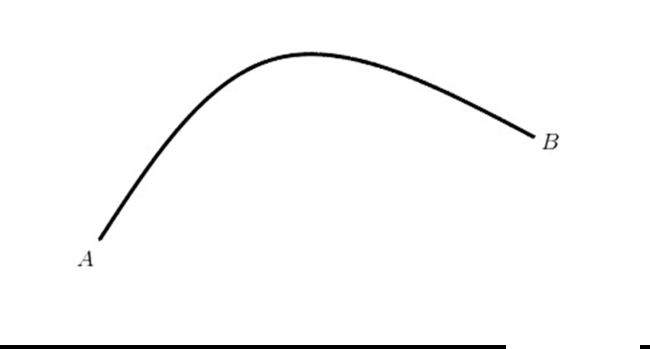
比如我们想知道曲线 A B \boldsymbol{AB} AB 上任一点处的弯曲程度怎么办呢?这时就需要一个十分重要的概念——曲率。
维基百科:
- 在数学中,
曲率(curvature)是描述几何体弯曲程度的量,例如曲面偏离平面的程度,或者曲线偏离直线的程度。在不同的几何学领域中,曲率的具体定义不完全相同。曲率可分为外在曲率和内蕴曲率,二者有重要的区别。前者的定义需要把几何体嵌入到欧式空间中,后者则是直接定义在黎曼流形上。- 曲线的曲率通常是标量,但也可以定义曲率向量。对于更复杂的对象(例如曲面,或者一般的 n 维空间),曲率要用更复杂的线性代数来描述,例如一般的黎曼曲率张量。
曲率包含的知识点很多,如下所示:
1.1 弧长参数 s
弧长参数又称为自然参数,该参数的引入是意义非凡的。一个最为明显的意义在于,弧长作为参数就是将参数赋予了几何意义,这样在几何意义上,就可以将参数和曲线本身统一起来。
那么现在就有一个问题了,为什么弧长可以作为参数? 说明这个问题之前我们需要先知道如何求一条曲线的弧长。
注: C 1 C^1 C1 类曲线是指光滑曲线。

我们按照上面的方式划分为 n \pmb{n} n 个小段,之后我们用直线将相邻的两个点连结起来,最后会得到一条折线,这条折线的长度记为:
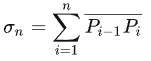
取 λ n = max a ≤ t ≤ b { t i − t i − 1 } \lambda_n=\max_{a\leq t\leq b}\{t_i-t_{i-1}\} λn=maxa≤t≤b{ti−ti−1},并使 lim n → + ∞ λ n = 0 \lim_{n\to +\infty}\lambda_n=0 limn→+∞λn=0,此时 σ n \sigma_n σn 趋于一共与分点无关的确定的极限 σ \sigma σ ,这个极限我们就定义为曲线 P 0 P n \pmb{P}_0\pmb{P}_n P0Pn 的长度,即:
![]()
图解数学
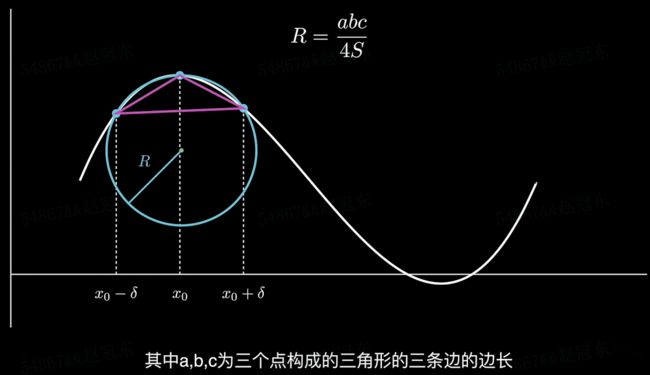
其中, a \pmb{a} a、 b \pmb{b} b、 c \pmb{c} c 为三个点构成的三角形的三条边的边长, S \pmb{S} S 为这个三角形的面积。
将三条边分别用向量 a ⃗ \pmb{\vec{a}} a、 b ⃗ \pmb{\vec{b}} b、 c ⃗ \pmb{\vec{c}} c 表示。则三条边的边长就是三个向量取模长。
由与所构成的平行四边形的有向面积,可以用行列式 d e t ( a , b ) \pmb{det}(a,b) det(a,b)表示(行列式的性质)。因为是有向面积,取绝对值后,得到的 ∣ d e t ( a , b ) ∣ \left| \pmb{det}(a,b) \right| ∣det(a,b)∣ 才是有效面积。
三角形的面积等于这个平行四边形的一半。
假设曲线为 f \pmb{f} f,根据这个公式,就可以算出 R \pmb{R} R,

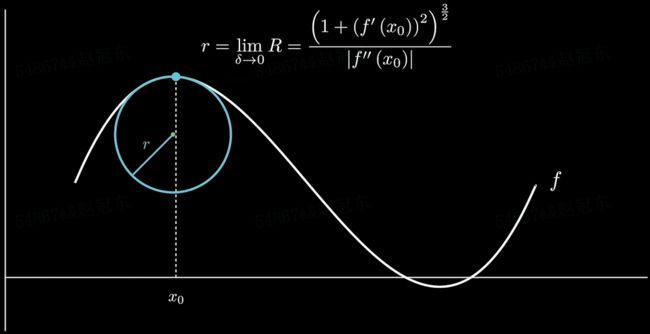
下面让左右两边的点,向中间靠拢:
设 δ \pmb{\delta} δ 趋于 0 时,得到的密切圆半径为 r \pmb{r} r,则 r \pmb{r} r 为 R \pmb{R} R 的极限。
Python 中的曲线曲率

曲率是曲线偏离直线的量度。例如,圆的曲率是半径的倒数,而直线的曲率是 0 。
在本教程中,我们将学习如何使用 numpy 模块在 Python 中计算曲线的曲率。我们还将计算其他量,例如速度,加速度等。你可以在下面的图片中找到必要的公式。
import numpy as np
import matplotlib.pyplot as plt
coordinates = np.array([[1, 1], [1.5, 2], [2, 3], [2.5, 3.5], [3, 4], [3.5, 4.25], [4, 4.5]])
plt.plot(coordinates[:, 0], coordinates[:, 1])
输出:
对于与曲线有关的此类问题,我们需要计算给定曲线在每个点的导数。在这种情况下使用 numpy.gradient() 方法,该方法返回 N 维数组的梯度。
在下面的代码中,我们计算所有点的曲线速度。
x_t = np.gradient(coordinates[:, 0])
y_t = np.gradient(coordinates[:, 1])
vel = np.array([[x_t[i], y_t[i]] for i in range(x_t.size)])
print(vel)
输出:
[[0.5 1. ]
[0.5 1. ]
[0.5 0.75 ]
[0.5 0.5 ]
[0.5 0.375]
[0.5 0.25 ]
[0.5 0.25 ]]
在计算速度之后,我们继续进行速度。现在,速度就是速度的模数。但是,应该知道,到目前为止,所有事物都是 t \pmb{t} t 的函数( t \pmb{t} t 表示时间间隔)。因此,我们将在每一秒的时间间隔内将速度表示为数值的 numpy 数组。
请参见下面的代码。
speed = np.sqrt(x_t * x_t + y_t * y_t)
print(speed)
输出:
[1.11803399 1.11803399 0.90138782 0.70710678 0.625 0.55901699 0.55901699]
现在,为了计算切线,我们将执行一些变换,以确保速度和速度的大小相同。同样,我们需要能够将矢量值速度函数除以标量速度数组。
tangent = np.array([1/speed] * 2).transpose() * vel
print(tangent)
输出:
[[0.4472136 0.89442719]
[0.4472136 0.89442719]
[0.5547002 0.83205029]
[0.70710678 0.70710678]
[0.8 0.6 ]
[0.89442719 0.4472136 ]
[0.89442719 0.4472136 ]]
同样,我们现在可以隔离切线的分量并计算其梯度以找到法线向量。
现在,我们将在下面的代码中实现提供的曲率公式。
ss_t = np.gradient(speed)
xx_t = np.gradient(x_t)
yy_t = np.gradient(y_t)
curvature_val = np.abs(xx_t * y_t - x_t * yy_t) / (x_t * x_t + y_t * y_t)**1.5
print(curvature_val)
输出:
[0. 0.04472136 0.17067698 0.26516504 0.256 0.17888544 0. ]
参考资料
[1] 什么是曲率?什么又是挠率?2019.7;
[2] 计算离散点的曲率(附Python, MATLAB代码)2021.3;