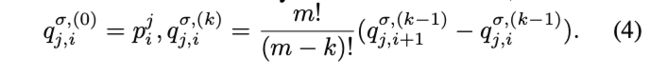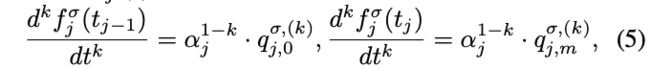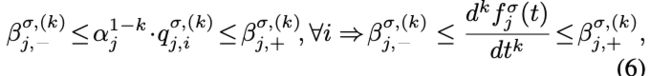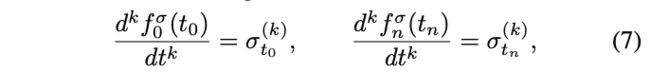【论文解读】在复杂城市环境中基于时空语义走廊的安全轨迹生成
标题:Safe Trajectory Generation for Complex Urban Environments Using Spatio-temporal Semantic Corridor
作者:Wenchao Ding, Lu Zhang, Jing Chen, and Shaojie Shen
来源:https://arxiv.org/abs/1906.09788
代码:https://github.com/HKUST-Aerial-Robotics/EPSILON
文章目录
- 前言
- 一、简介
- 二、系统框架
- 三、多方针决策的准备
- 四、时空语义走廊
-
- 4.1 语义元素和 Frenet 坐标系
- 4.2 语义走廊的生成
- 五、安全可行的轨迹生成
-
- 5.1 贝塞尔曲线及其性质
- 5.2 分段贝塞尔曲线
- 5.3 强制安全和动态约束
- 六、 实验结果
前言
在复杂的城市环境中自动驾驶汽车的轨迹规划是极具挑战性的,因为需要考虑到许多语义的元素,比如动态代理、交通信号灯和速度限制。这些语义元素可能有不同的数学描述,例如障碍、约束和成本。调整不同语义元素组合来获得稳定和可概述的行为并非易事。
在本文中,我们提出了一种新颖的统一时空语义走廊(SSC)结构,它为不同类型的语义元素提供了一定程度的抽象。 SSC 由一系列相互连接的无碰撞立方体组成,动态约束由时空域中的语义元素构成。轨迹生成问题归结为一般二次规划 (QP) 公式。由于统一的 SSC 表示,我们的框架可以推广到语义元素的任何组合。此外,我们的公式通过使用分段贝塞尔曲线参数化的凸包和 Hodograph 特性提供了整个轨迹安全且满足约束的理论保证。
注:凸包特性是指贝塞尔曲线被完整地限制在控制点所形成的凸包内,Hodograph特性是指Bezier曲线B()的导数曲线B’()被称为Hodograph,还是贝塞尔曲线。
一、简介
由于复杂的城市环境中包含许多语义元素(交通灯、限速标志、停车标志等等),要想为自动驾驶汽车生成安全可执行的轨迹并不是件简单的事情。不同类型的语义元素可能数学表述也是不一样,调用不同类型的语义元素来进行组合也并非易事。我们需要使用一种统一的方式来描述各种语义元素,让规划的性能不会受到语义元素的类型和组合的影响。
除了语义元素的表示问题外,另一个问题是如何保证生成轨迹的安全性和可行性。现在大多数的基于优化或者基于状态栅格图的运动规划器会尝试在一系列的采样点中检查或强制执行约束,这样可能会导致无法检测到两个采样点之间的不可行点,会为整条轨迹的生成带来安全隐患。
为了克服上述挑战,我们提出了一个具有理论安全性和可行性保证的统一轨迹生成框架。 该框架的关键是一种新颖的时空语义走廊(SSC)结构。 SSC 的目的是大多数语义元素可以呈现为时空障碍或时空域特定范围内的约束。SSC 的关键特性是它对不同类型的语义元素的抽象。 本质上,SSC 由一系列相互连接的无碰撞立方体组成,具有由语义元素构成的动态约束。 我们提出了一个 SSC 生成过程来生成和拆分立方体,以便可以正确关联动态约束。
在给定统一的 SSC 表示下,轨迹生成问题归纳为在满足动态约束条件下在 SSC 内生成最优轨迹。在本文中,我们提供了一种二次规划(QP)公式,该公式是通过使用分段贝塞尔曲线参数化来保证生成轨迹的安全性和可行性,该公式建立在 Bezier 曲线的凸包和Hodograph特性上。
主要的贡献总结如下:
- 新颖的时空语义走廊 结构,为复杂城市环境中的各种语义元素提供统一表示。
- 基于优化的轨迹生成公式,确保整个生成轨迹的安全性和可行性。
- 一个完整的开源轨迹生成框架,并在多智能体城市模仿真平台中实时实现,并提供了全面的实验和比较来验证性能。
二、系统框架
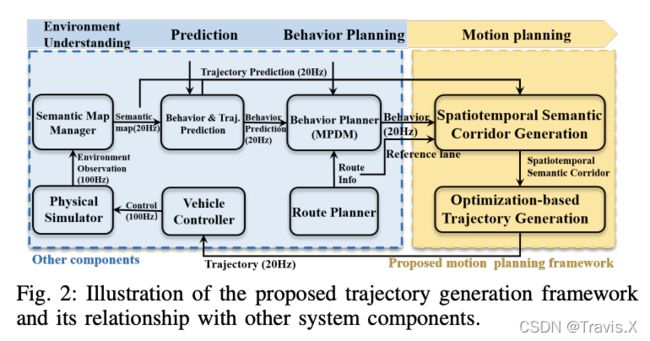
我们提出的轨迹生成框架属于的是自动驾驶汽车的运动规划层,它需要来自上游的必要输入,例如行为层。 除了介绍轨迹生成之外,还会简单介绍下其他的系统组件,以阐明我们框架的输入和输出。
如图 2 所示,一个规划周期分为四个阶段。
- 第一阶段是语义地图管理器来获得对环境的理解,该管理器负责管理语义元素(例如,占用网格地图、动态代理、车道、交通规则等)用作局部规划。
- 第二阶段是预测,它不仅提供高级行为预测(例如,变道、保持车道等),还预测其他动态代理的轨迹。
- 第三阶段是行为规划,使用多策略决策 (MPDM) 方法实现。
- 第四阶段是我们提出的运动规划,它将行为规划器的离散未来模拟状态作为走廊生成的种子。请注意,我们的轨迹生成框架也可以与其他行为规划器共同使用,只要行为规划器能提供对未来状态的初步猜测。
要构建 SSC,需要四个要素,即由语义元素组成的语义图、动态代理的预测轨迹、前向的模拟状态和由路线信息给出的参考车道。 请注意,如果前向模拟状态已经包括其他代理的状态,例如 MPDM 的情况,则轨迹预测模块可能是可选的。 在这种情况下,我们可以使用其他车辆的模拟状态作为预测轨迹,这有助于将交互预期从行为规划传递到运动规划层。 然而,由于这不是行为规划中的常见特征,为了通用性,我们仍然在实验中使用来自轨迹预测模块的预测轨迹,这可能会丢失行为规划中的交互信息。 总而言之,种子的来源和交互的建模取决于行为规划者的选择。
三、多方针决策的准备
在本文中,我们采用 MPDM 作为行为层,轨迹生成方法也可以与其他行为规划方法一起使用。本节简单介绍下 MPDM。
MPDM 模型将行为规划问题表述为通用的多智能体部分可观察马尔可夫决策过程 (POMDP),以对动态环境中的交互和不确定性进行建模。 由于车辆数量增加时求解 POMDP 很快变得难以计算,所以 MPDM 放宽了这个问题并假设我们的车辆和其他代理都在执行一组有限的闭环离散策略(例如,变道、保持车道等等)。 此外,对于每个闭环策略,通过使用简化的仿真模型对所有车辆状态进行前向模拟来预测未来情况,例如理想化的转向和速度控制器。 设计了一个全面的奖励函数来评估未来的情况并选出最佳的行为。
在本文中,我们使用车辆的前向模拟状态作为走廊生成过程的种子。 尽管初始种子是无碰撞的,但由于分辨率粗(实验中为 0.15 s)和简化的仿真模型(例如,实验中的分段线性控制),它们不能直接由车辆执行。
由于 MPDM 同时为多种行为(例如左变道、右变道和保持车道)提供了前向模拟状态,我们充分利用这一特性,为所有潜在的行为生成候选轨迹,以增强模型的鲁棒性。 例如,在执行换道轨迹时,我们的轨迹框架总是准备切换回原始车道的轨迹,如图 3 所示。

四、时空语义走廊
4.1 语义元素和 Frenet 坐标系
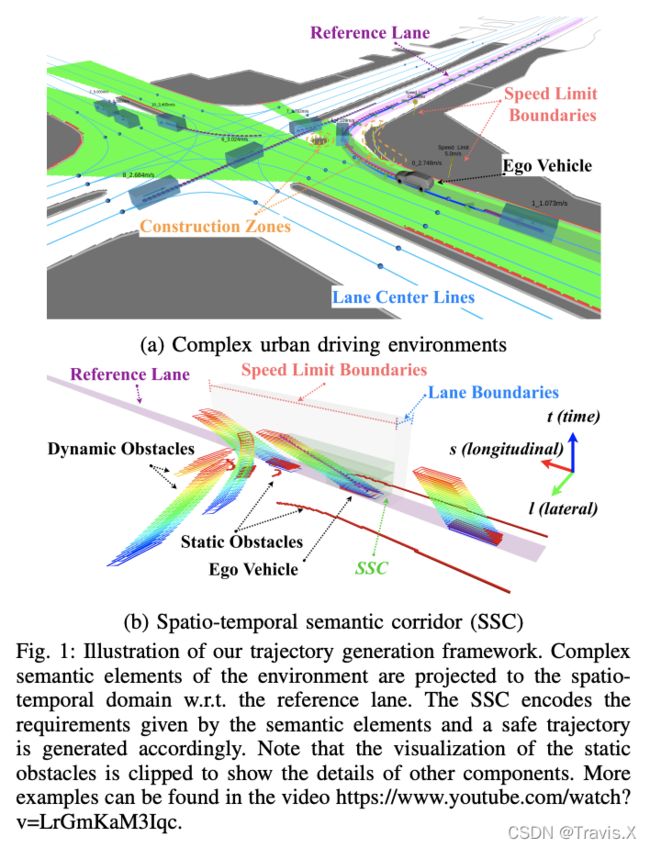
我们需要用到的是一个由纵向 s、横向 l 和时间 t 组成的 slt 3-D 配置空间。纵向和横向方向是相对于 Frenet 坐标系的,它是由参考的车道线构建的动态参考框架。通常,参考车道是从路线规划器提供的路线信息中提取的,如图 2 所示。对于没有可用车道的非结构化环境,参考车道也可以由路径规划器提供。
我们不在笛卡尔坐标中生成走廊,而是采用 Frenet 框架表示,是因为大多数语义元素与车道几何相关联。 例如,限速、交通灯和停车标志通常与车道的某个纵向范围相关联。 此外,由于类人驾驶行为通常可以解耦为横向运动和纵向运动,因此对这两个方向的自由空间进行建模比在笛卡尔坐标中建模自由空间更自然。 时间是另一个必要的维度,因为许多语义元素都是时间索引的。 例如,预测轨迹是时间分布的,可以看作是一系列时空障碍。
图 1 和图 3 分别描述了将语义元素投影到 Frenet 框架的两个典型示例。 多种语义元素一般可以分为两类:Obstacle-like语义元素和 Constraint-like 语义元素。
-
Obstacle-like:很多语义元素是具备物理意义,不允许slt域的某一部分进入。例如,静态障碍物可以被视为跨越整个时间轴的障碍物,动态障碍物可以被视为 根据预测的轨迹在时域中作为一系列静态障碍物,而红灯可以渲染为占据特定纵向位置和时间段的障碍物。 在将类似障碍物的语义元素渲染到 slt 域之后,配置空间是一个 3-D 占用网格。
-
Constraint-like :除了 Obstacle-like 语义元素外,许多语义元素表示动态约束或时间约束。 例如,速度限制和停车标志可以被视为速度限制。 还有一些语义元素会造成时间限制。 例如,在交叉车道时,换道的总时间不应过长。
我们为所有 Constraint-like 的语义元素提出了一个统一的表示,即语义边界。 例如,可以将速度限制视为应用于纵向范围 [sbegin, send] 的速度约束,其中 sbegin 和 send 是两个语义边界。 变道持续时间约束可以看作是应用于当前车道的横向范围[dbegin,dend]的时间约束。 本质上,语义边界表示某个语义元素开始和停止生效的位置。
注意,在约束的“硬度”方面存在细微差别。 具体来说,交通规则(例如,速度限制)带来的是硬约束,是必须遵守的。 自然的类人行为需要其他约束(例如,变道持续时间约束),并且没有对此类约束的通用定量描述。 我们在走廊生成过程中考虑了其中的差异。
4.2 语义走廊的生成
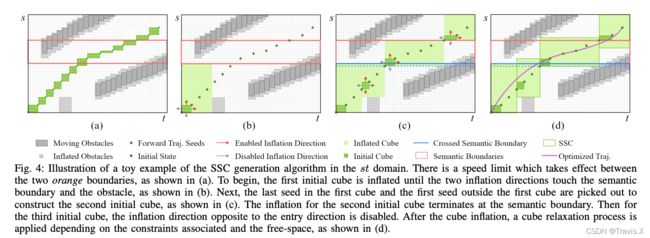
算法概述。如下图所示,生成过程包括种子生成、立方体膨胀、约束关联和立方体松弛。

1)种子生成:语义走廊的种子是通过将行为规划器的前向模拟状态投影到slt配置空间来生成的。 由于前向模拟状态是离散化的,因此走廊生成过程的可行性取决于环境的复杂性和种子分辨率。 为了保证走廊生成过程的成功,我们要求由连续种子构建的初始立方体是无碰撞的。 在实践中,这个间隙要求是合理且容易实现的。
围绕种子生成走廊的动机是对拓扑等效的自由空间进行完全建模,同时保留相同的高级行为。 例如,如图4(a)所示,种子的语义是在两个动态障碍物之间通过,由走廊生成保留。 由于运动规划器应该使用任何给定的初始状态,初始状态也应该包含在种子中。
2)带有语义边界的立方体膨胀:走廊是通过迭代种子生成的。已经包含在最后一个膨胀的立方体中的种子会被跳过(第 4 行,算法 2),因为它们在拓扑上是等价的。初始立方体是基于两个连续种子生成的,将两个种子视为两个立方体顶点(第 5 行,算法 2)。
立方体膨胀的关键特征是考虑语义边界(第 9 行,算法 2)。立方体膨胀过程的目标是生成与语义边界匹配的立方体,以便可以方便地关联约束。具体来说,当初始立方体与某个语义边界相交时,与入口方向相反的膨胀方向被禁用,使得膨胀后的立方体几乎可以匹配语义边界。对于一个膨胀步骤,膨胀在三个 slt 方向之间交替,如果该步骤与障碍物碰撞或与某个语义边界相交,则膨胀终止。图 4 (b) 和 © 中提供了一个玩具示例。由于在优化(第 VI 节)中,每个立方体对应于轨迹的一个片段,并且为了保持凸性,我们没有显式优化片段的持续时间,当前立方体的时间上限应该与轨迹的时间下限一致下一个立方体。可以考虑优化持续时间(非凸),在这种情况下,进一步膨胀以增加 t 维度的重叠可能是有益的。

3)立方体松弛:经过立方体膨胀过程,膨胀的立方体几乎匹配语义边界,如图4(c)所示。 然而,正如 V-A2 中提到的,一些约束,例如车道变换持续时间约束是软约束,应该留出额外的空间进行优化。 为此,我们采用立方体松弛过程来松弛立方体边界,同时保留硬约束和无碰撞特性,如图4(d)所示。 松弛允许的最大余量由应用于两个连续立方体的约束系统地确定。 例如,在纵向上,可以根据速度约束通过速度匹配距离来确定边距。 对于横向(即换道情况),可以通过换道持续时间的允许波动来计算余量。
五、安全可行的轨迹生成
给定 SSC 指定的约束条件,我们提出了一种基于优化的轨迹生成方法,该方法可以在 SSC 内找到最优轨迹,同时满足动态约束。 优化问题也是在 Frenet 坐标系下制定的,这与 SSC表示是一致的。 一般情况下根据最优控制理论对纵向和横向会使用五次多项式多项式。 然而,五次多项式多项式不适用于 SSC 中的优化,原因如下:
- 多项式的一部分仅具有有限的表示能力,可能无法表示 SSC 所需的高度约束的机动;
- 多项式不太适合具有复杂配置空间障碍和动态约束的问题。 在先前关于单项式多项式轨迹的工作中,约束仅在有限的一组采样点上强制执行/检查。 但是,这种方法可能无法检测到采样点之间的碰撞,因此无法保证安全性和可行性。
在本文中,我们通过对沿参考车道的二维轨迹(即纵向 s(t) 和横向 l(t))使用分段贝塞尔曲线来消除上述两个限制。 使用分段贝塞尔曲线的原因是它的凸包特性和 Hodograph 特性。
5.1 贝塞尔曲线及其性质
m阶的贝塞尔曲线 f ( t ) f(t) f(t) 由 m + 1 m + 1 m+1 个控制点在固定区间 t ∈ [ 0 , 1 ] t ∈ [0, 1] t∈[0,1] 上定义如下:
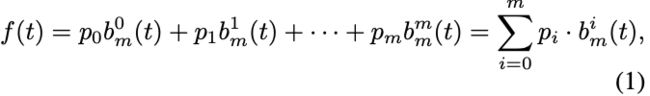
其中 p i p_i pi 表示控制点,用 P P P表示控制点集 [ p 0 , p 1 , . . . , p m ] [p_0, p_1, . . . , p_m] [p0,p1,...,pm]。
凸包性质适用于将曲线约束在凸自由空间中的问题。 具体来说,贝塞尔曲线 f ( t ) f(t) f(t)保证完全限制在由控制点 P P P 支持的凸包中。 换句话说,通过将 P约束在凸自由空间内,可以保证得到的曲线是无碰撞的。
hodograph 性质有助于约束 Bezier 曲线的高阶导数,这对于强制执行动态约束很有用。根据 hodograph 特性,贝塞尔曲线 d f ( t ) d t {df(t) \over d_t} dtdf(t) 的导数是另一条贝塞尔曲线,其控制点为 p i ( 1 ) p ^{(1)} _i pi(1) = m ⋅ ( p i + 1 − p i ) m · (p_{i +1} − p_i) m⋅(pi+1−pi)。 通过在求导后的贝塞尔曲线上应用凸包特性,可以将原始曲线 f ( t ) f(t) f(t) 的整个动态轮廓限制在给定的动态范围内,如图 5 所示。
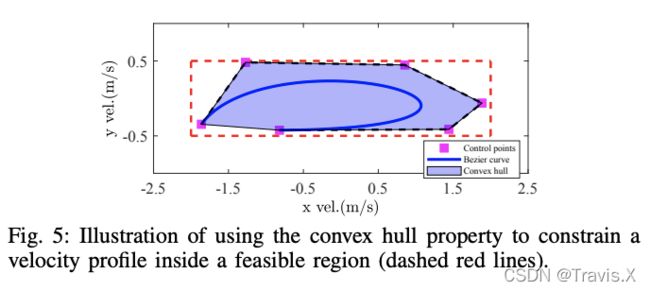
5.2 分段贝塞尔曲线
在本文中,我们采用分段贝塞尔曲线表示每一块都与 SSC 的一个立方体相关联。
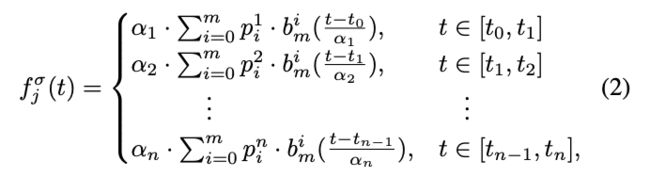
其中 p j i p_j^i pji 表示第 j 段的第 i 个控制点, t 0 , t 1 , . . . , t n t_0, t_1, . . . , t_n t0,t1,...,tn 是每个段的起点和终点的时间戳。 由于贝塞尔曲线在固定间隔 [0, 1] 上定义,而每个段的轨迹持续时间可能会有所不同,因此我们根据每个段的持续时间为每个段引入比例因子 α j α_j αj。
我们最小化由 jerk 平方的时间积分给出的代价函数。 具体来说,第 j 段的代价 J j J_j Jj 可以写作:
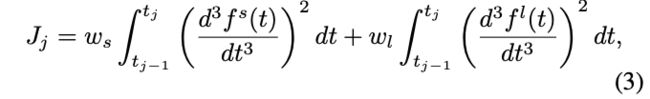
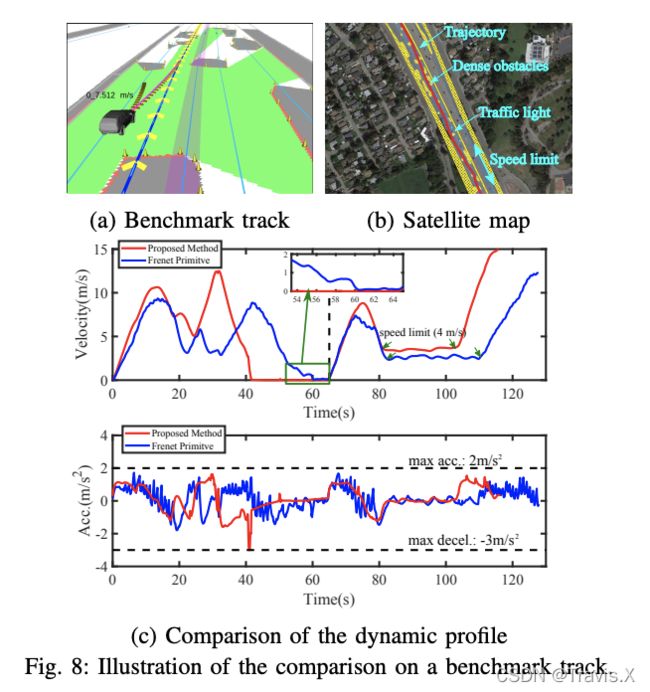
其中 w s w_s ws 和 w l w_l wl 分别表示纵向和横向控制代价的权重。 由于 SSC,目标是简单且不变的,因为 SSC 使得语义元素的不同组合可以轻松适应不同的流量配置。 用 y j σ ( t ) y_{j} ^σ (t) yjσ(t) 表示区间 [0, 1] 中的非缩放贝塞尔曲线,以 p j p_j pj 作为控制点。 令 u = t − t j − 1 α j t−t_{j−1} \over α_j αjt−tj−1 表示非缩放贝塞尔曲线的归一化时间,可以使用非缩放 y j σ ( t ) y^σ_j (t) yjσ(t) 重写 σ 维上的第 j 段的代价,如下所示: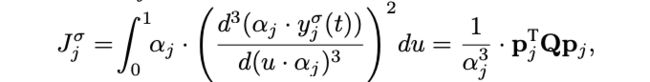
其中 Q 是非缩放贝塞尔曲线的 Hessian 矩阵。处于简洁的目的,我们省略了 Q 的详细计算。
5.3 强制安全和动态约束
在本文中,我们采用五次(m=5)分段贝塞尔曲线作为轨迹参数化。 根据 hodograph 特性,非标度贝塞尔曲线的 k 阶导数 ´ d ky σ j (t) dtk 由控制点 q σ,(k) j 支持,控制点 q σ,(k) j 可以通过归纳计算如下: