多机器人路径规划CBS/ECBS等 libmultiRobotPlanning 代码阅读笔记
编译后会生成doc的doxygen的html文件,帮助对程序的理解。
CBS 的容易理解的一个博客:CBS多机器人规划–深一
cbs.hpp 中 search 函数结构为:
1、首先构建start节点,其中包含了空solution,空constrains,cost =0和id=0。
2、调用低层次搜索,产生初始解填补 start.solution.
3、构建最小堆open,并且将初始节点压入堆
4、弹出open堆中代价最小的节点P直至open为空
5、对P中的solution进行冲突检查
6、无冲突则返回solution,有冲突则创建相应的约束,并且构建新的节点NewNode, NewNode = P,但是需要增加新的约束。然后有一个减去代价的操作(未理解,可能是因为,上个节点不能用,所以需要回退到前一个,所以代价需要相应减少,在lowLevel.search中有计算每个解的代价,可以去看看)
发生冲突的路径,假设对A机器人和B机器人搜索的路径分别是 P A P_A PA和 P B P_B PB,对应的代价分别是 C A C_A CA和 C B C_B CB,发生冲突后,就需要添加约束重新搜索,比如是对A进行重新搜索,那确实是需要减去代价 C A C_A CA的
7、对NewNode进行低层次搜索,若成功搜索到路径,然后加入open堆中,跳至4。
高层次搜索:检测冲突并且构建约束树。
CBS serach 中调用低层次的搜索产生路径如下:为每个机器人搜索产生路径,失败的话直接返回false.第层次搜索是在有约束的基础上只搜索路径,不会检测是否有冲突。因此如果在构建好的约束上去搜索,没有路径。那直接失败。
for (size_t i = 0; i < initialStates.size(); ++i) {
// if ( i < solution.size()
// && solution[i].states.size() > 1) {
// start.solution[i] = solution[i];
// std::cout << "use existing solution for agent: " << i << std::endl;
// } else {
LowLevelEnvironment llenv(m_env, i, start.constraints[i]);
LowLevelSearch_t lowLevel(llenv);
bool success = lowLevel.search(initialStates[i], start.solution[i]);
if (!success) {
return false;
}
// }
start.cost += start.solution[i].cost;
}
对open列表循环检测。open 是约束节点队列
根据路径,利用Environment中成员函数getFirstConfilict检查冲突,无冲突返回true。
Conflict conflict;
if (!m_env.getFirstConflict(P.solution, conflict)) {
std::cout << "done; cost: " << P.cost << std::endl;
solution = P.solution;
return true;
}
对于每个节点根据冲突增加约束,然后再进行搜索,直至while(!open.empty())不成立,或者是路径检查后无冲突。
m_env.createConstraintsFromConflict(conflict, constraints);
for(const auto& c : constrains)
{
....
}
example中的cbs等,对应multi_trajectory中的environment.h
整体结构并不是难以理解,但是现在疑问
1) 如何有约束的A *搜索路径; 2) Environment的设置,如何确定冲突;3)约束的建立
Answer 2) Environment的结构定义是在cbs.cpp文件中 Class Environment
环境的初始化函数包括了维度信息,比如4X4栅格,障碍物位置,目标位置,disappearAtGoal默认是false,指的是,到达目标点后就消失,怪不得不会检测目标点是否一样导致的冲突呢
Answer 3) 约束建立:
冲突的结构(源码还有一些运算符重载):
struct Conflict {
enum Type {
Vertex,
Edge,
};
int time;
size_t agent1;
size_t agent2;
Type type;
int x1;
int y1;
int x2;
int y2;
}
节点冲突结构(源码中同样有重载):
struct VertexConstraint {
int time; int x.; int y;}
边冲突结构:
struct EdgeConstraint {
EdgeConstraint(int time, int x1, int y1, int x2, int y2)
: time(time), x1(x1), y1(y1), x2(x2), y2(y2) {}
int time;
int x1;
int y1;
int x2;
int y2;
}
带有约束的A搜索,但是好像并不是A,代码中没有启发式的计算过程。而且另外一点,因为包含了约束,所以启发函数只用欧式距离可能并不能保证最优。
另外其最优解应该是用stl标准库的unordered_map找到的。
根据冲突建立约束,包括两类约束:
vertex constraint 和 edge constraint ,其中和冲突一样。
cbs.cpp中函数creatConstraintsFromConflict()为实际创建约束的函数,主要区别是增加了对agent的约束,两个结构体只是表示,在某个时间不能在顶点A 或者 不能从顶点A到顶点B
void createConstraintsFromConflict(
const Conflict& conflict, std::map<size_t, Constraints>& constraints) {
if (conflict.type == Conflict::Vertex) {
Constraints c1;
c1.vertexConstraints.emplace(
VertexConstraint(conflict.time, conflict.x1, conflict.y1));
constraints[conflict.agent1] = c1;
constraints[conflict.agent2] = c1;
} else if (conflict.type == Conflict::Edge) {
Constraints c1;
c1.edgeConstraints.emplace(EdgeConstraint(
conflict.time, conflict.x1, conflict.y1, conflict.x2, conflict.y2));
constraints[conflict.agent1] = c1;
Constraints c2;
c2.edgeConstraints.emplace(EdgeConstraint(
conflict.time, conflict.x2, conflict.y2, conflict.x1, conflict.y1));
constraints[conflict.agent2] = c2;
}
}
变量constraints是map对象,c1是冲突变量,即在某个时刻不能在某点,或在不能穿过某条边。当为顶点冲突时,只需要对产生冲突的1,2智能体分别添加约束,即constraints[agent1/2] = c1. 当为边冲突时,由于agent1是A->B, agent2是B->A,所以添加的约束不同。agent1是不能在t时刻,从(x1,y1)->(x2,y2),agent2 是不能从(x2,y2)->(x1,y1)。注意:对车辆1建立约束,则边冲突(即交换位置产生的冲突,车辆1的位置在前
这里注意 constraints 是变量名,Constrains时结构体名
*Answer 1) *
A_star.cpp中,Node节点结构为:
struct Node {
Node(const State& state, Cost fScore, Cost gScore)
: state(state), fScore(fScore), gScore(gScore) {}
bool operator<(const Node& other) const {
// Sort order
// 1. lowest fScore
// 2. highest gScore
// Our heap is a maximum heap, so we invert the comperator function here
if (fScore != other.fScore) {
return fScore > other.fScore;
} else {
return gScore < other.gScore;
}
}
friend std::ostream& operator<<(std::ostream& os, const Node& node) {
os << "state: " << node.state << " fScore: " << node.fScore
<< " gScore: " << node.gScore;
return os;
}
State state;
Cost fScore;
Cost gScore;
初始化中,第一个是状态,第二个是F=G+H中的F,第三个是G
State是在cbs.cpp中定义的结构体,包括当前时间和位置,time, x,y
邻居的定义,启发式信息是什么,每个状态和action ,如何满足约束
A* 搜索
普通A* 流程
把起点加入 open list 。
重复如下过程:
a. 遍历 open list ,查找 F 值最小的节点,把它作为当前要处理的节点。
b. 把这个节点移到 close list 。
c. 对当前方格的 8 个相邻方格的每一个方格?
◆ 如果它是不可抵达的或者它在 close list 中,忽略它。否则,做如下操作。
◆ 如果它不在 open list 中,把它加入 open list ,并且把当前方格设置为它的父亲,记录该方格的 F , G 和 H 值。
◆ 如果它已经在 open list 中,检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好,用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样,把它的父亲设置为当前方格,并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话,改变后你可能需要重新排序。
d. 停止,当你
◆ 把终点加入到了 open list 中,此时路径已经找到了,或者
◆ 查找终点失败,并且 open list 是空的,此时没有路径。
3.保存路径。从终点开始,每个方格沿着父节点移动直至起点,这就是你的路径。
在带有约束的搜索中,主要是
首先创建open_set,并且把初始状态,以及对应的F和G值作为一个节点push进openSet中。
初始的G即为0,所以初始F即为H,这里的启发式函数是曼哈顿距离。
然后放入stateToHeap中,stateToHeap 和openSet是一样的,根据源码猜测,openSet是用来排序,然后找到最小代价的,stateToHeap是用来根据句柄查找的,检测扩展的节点信息是否在openSet中。(map的查询复杂度O(1))
查询openSet中F值最小的,由于采用最小堆,所以top的就是最小的
检查检查终点是否在open_list中,如果在,就对之前的solution进行clear,然后重新push_back,返回路径。如下:
if (m_env.isSolution(current.state)) {
solution.states.clear();
solution.actions.clear();
auto iter = cameFrom.find(current.state);
while (iter != cameFrom.end()) {
solution.states.push_back(
std::make_pair<>(iter->first, std::get<3>(iter->second))); //-- 状态和G值
solution.actions.push_back(std::make_pair<>(
std::get<1>(iter->second), std::get<2>(iter->second)));//-- Action和F值
iter = cameFrom.find(std::get<0>(iter->second)); //--find状态(应该是父节点)
}
solution.states.push_back(std::make_pair<>(startState, initialCost));
std::reverse(solution.states.begin(), solution.states.end());
std::reverse(solution.actions.begin(), solution.actions.end());
solution.cost = current.gScore;
solution.fmin = current.fScore;
return true;
}
如果不是终点,那就把当前节点从open_list中除去pop,然后在close_list中加入
openSet.pop();
stateToHeap.erase(current.state); //--在stateToHeap中删除当前节点的状态
closedSet.insert(current.state);
然后对当前节点扩展周围四连通区域,包括前进后退左右和wait,这个代码在
cbs.cpp文件中Environment class中。在增加状态时,会检查两类约束,stateValid()函数和transitionValid(s,n)
bool stateValid(const State& s) {
assert(m_constraints);
const auto& con = m_constraints->vertexConstraints;
return s.x >= 0 && s.x < m_dimx && s.y >= 0 && s.y < m_dimy &&
m_obstacles.find(Location(s.x, s.y)) == m_obstacles.end() &&
con.find(VertexConstraint(s.time, s.x, s.y)) == con.end();
}
bool transitionValid(const State& s1, const State& s2) {
assert(m_constraints);
const auto& con = m_constraints->edgeConstraints;
return con.find(EdgeConstraint(s1.time, s1.x, s1.y, s2.x, s2.y)) ==
con.end();
}
对满足约束的周围节点,检测是否已经进行过扩展(是否在close_list中),是否在open_list中,若不在open_list中,计算代价,然后填充到open_list和stateToHeap中
若在open_list中,则检查之前G值和当前G值,若之前>现在,进行更新
openSet.increase(handle); //--修改G和F值后,在open_set中重新排序,数据结构必须配置为可变的
然后放到cameFrom中,这个为了找到父节点,然后寻路的。
细节:有z方向,代表的是车头的朝向,其实就是改成了基元类型,禄五年中也有体现
安全走廊建立
就是对线段在x,y方向进行扩展,扩展成为正方形的
首先对每个线段进行分割,分成5个,具体原因论文中有体现:如果是整个线段,那如果线段的一部分扩展后有障碍,则整个都废了,但是分成小段,就会解决这个问题
主要函数是corridor.hpp中的uodateObsBox()
首先在corridor类构造函数中对N:轨迹点的数量,plan: 轨迹点的信息,位置,速度信息。当两个轨迹点之间距离小于0.1的时候,速度为0,距离在0.1-1.1时,为0.7的最大速度,当大于1.1时,为最大速度。
函数isObstacleInBox(),是遍历box中的点,以octomap的分辨率进行遍历,逐个进行遍历,查看该点到障碍物的距离,是否和膨胀后的智能体距离一样,从而看是否碰撞。
函数isBoxInBoundary(),看点box是否在地图中
函数expand_box(),对当前box,在xyz的6个方向上,以分辨率逐个进行扩展,直至碰到边缘(isBoxInBoundary())或者障碍(isObstacleInBox())后停止。
函数updateObsBox(),主要函数,在prioritized_traj_planner.cpp和couple_traj_planner.cpp中调用生成安全走廊。思路就是对相邻的两个点,选择最小的xyz作为box的下限,最大的xyz的box的上限。然后利用expand_box()函数对Box进行扩展。
优化
使用的其实是MPC进行优化的,目标函数如下
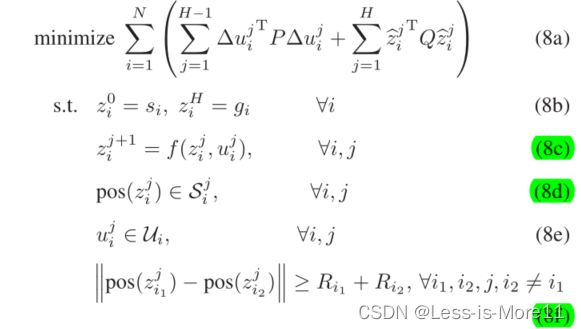
第一项是平滑性,表示速度差(也就是加速度)进行优化,第二项是和全局参考路径的差值,表示更接近参考路径。
约束项:满足起点和终点约束、满足动力学方程的约束、满足安全走廊的约束、控制量的约束,速度、加速度满足约束这种、和其他智能体的距离约束(要满足两者之间的距离大于两者半径和)。
优化思路用的是MPC,采用的IPOPT库进行优化。
IPOPT博客
MPC博客
带自己理解的注释的代码会放到github。
github链接:MultiRobtPlanning and trajectory planning