【自动驾驶轨迹规划之A*算法】
目录
1 A*算法简介
2 A*算法原理及流程
2.1 基本原理
2.2 算法流程
2.2.1 变量举例说明
2.2.2 算法流程图实例
3 算法测试地图
4 A*算法matlab实现
4.1 完善地图结构
4.2 方向自定义
4.3 A*算法
4.4 回溯
5 完整版A*算法
5.1 动画
5.2 完整源程序
1 A*算法简介
A*算法是一种静态路网中求解最短路径有效方法,也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近,最终搜索速度越快。A*算法的最大特点在于有启发性。
2 A*算法原理及流程
2.1 基本原理
具体算法原理请参考A*算法(超级详细讲解,附有举例的详细手写步骤)_Clark-dj的博客-CSDN博客_a*算法
这篇文章讲的非常详细,且有很多图与例子说明,本篇文章就不再赘述。
2.2 算法流程
2.2.1 变量举例说明
(1)open代表是不是待检查的节点,每次一个节点附近的八个节点都被设置为open=1
(2)close代表是不是不用再考虑,障碍物全初始化为close=1,若某个节点是八个节点中F最小 的,这个节点之后就不用再考虑,close=1
(3)从一个节点往八个方向走有八个格子,(ti,tj) 是第 t 个格子的坐标,t 在1~8范围内
(4)G代表从起点到这个节点的路径消耗,之前的每一步都会累加计算路径消耗,流程图中省略 了G(i,j)
(5)H代表从这个节点到目标点的路径消耗,可以用曼哈顿距离或欧式距离进行计算,流程图中 省略了H(i,j)
(6)father 代表了这个节点的父节点 (将二维坐标转化为行行相连的序号),有利于最后回溯得到 最短路径
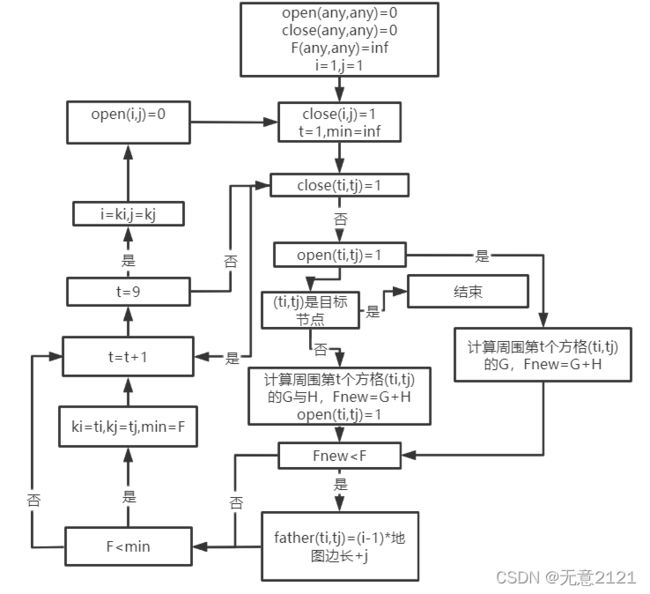
2.2.2 算法流程图实例
3 算法测试地图
参考 【自动驾驶轨迹规划自学笔记3】_无意2121的博客-CSDN博客
在那篇文章中还有更多的地图结构介绍,对A*算法的测试可以利用那篇文章的各种地图结构
本篇文章测试地图如下
将上面的图片转化为栅格地图的matlab代码如下
clc
clear all
Img=imread('C:\Autodesk\WI\ceshi.jpg');
Img = flipud(Img);%y坐标调换,由于读入图像时上下会反转
I = rgb2gray(Img);
a=50;b=50;% 设置网格格数 a表示横轴 b表示纵轴
length=1;%网格边长
B = imresize(I,[a/length b/length]);%对图像进行矩阵化
J=floor(B/(255-60));
%不接近白色的都变为黑色,即变成障碍物,这里的60是可以调整的范围,不同的图像有不同的处理方法
hold on;grid on;%添加网格线
axis([0,a,0,b]);
% gca表示当前绘图区域
% xtick表示x轴坐标刻度,刻度为0到a,步进为1
set(gca,'xtick',0:1:a,'ytick',0:1:b);
axis image xy
% 障碍物填充为黑色
for i=1:a/length-1
for j=1:b/length-1
if(J(i,j)==0)
y=[i,i,i+1,i+1]*length;
x=[j,j+1,j+1,j]*length;
h=fill(x,y,'k');
hold on
end
end
end4 A*算法matlab实现
4.1 完善地图结构
将地图的周围一圈设置成障碍物,使得路径规划在地图内,因此需要将整个地图往x轴正方向移动一格,往y轴正方向移动一格,matlab代码如下
%J(i,j)=0代表此处是障碍物,J(i,j)=1代表此无障碍物
%将地图整体向x轴正方向移动一格
for i=1:a/length-1
for j=b/length-1:-1:1
J(i,j+1)=J(i,j);
end
end
%将地图整体向y轴正方向移动一格
for i=a/length-1:-1:1
for j=2:b/length
J(i+1,j)=J(i,j);
end
end
%周围一圈设置成障碍
j=1;
for i=1:a/length+1
J(i,j)=0;
end
j=a/length+1;
for i=1:a/length+1
J(i,j)=0;
end
i=1;
for j=1:b/length+1
J(i,j)=0;
end
i=b/length+1;
for j=1:b/length+1
J(i,j)=0;
end4.2 方向自定义
栅格地图可以朝八个方向走,也可以朝四个方向走,代码如下
function [x,y,p]=direct(x,y,n)
if n==1
x=x+1;
p=1;
elseif n==2
y=y+1;
p=1;
elseif n==3
x=x-1;
p=1;
elseif n==4
y=y-1;
p=1;
elseif n==5
x=x+1;
y=y+1;
p=sqrt(2);
elseif n==6
x=x+1;
y=y-1;
p=sqrt(2);
elseif n==7
x=x-1;
y=y+1;
p=sqrt(2);
elseif n==8
x=x-1;
y=y-1;
p=sqrt(2);
else
x=x;
y=y;
end4.3 A*算法
A*算法实现起点到目标点的全局最优路径规划,在此过程中需要记录最短路径通过的节点,代码如下
i=2;j=2;%起点坐标,注意此时的坐标整体向右上方移动
XX=(i-1)*(a/length+1)+j;%起点行行连接的顺序
X1=47;Y1=6;%终点坐标
%画出起点和终点
y=[j-1,j-1,j,j]*length;
x=[i-1,i,i,i-1]*length;
h=fill(x,y,'y');
hold on;
y=[X1-1,X1,X1,X1-1]*length;
x=[Y1-1,Y1-1,Y1,Y1]*length;
h=fill(x,y,'g');
hold on;
%初始化
open=zeros(a/length+1,a/length+1);
close=1.-J;
close(i,j)=1;
G=zeros(a/length+1,a/length+1);
H=zeros(a/length+1,a/length+1);
F=zeros(a/length+1,a/length+1);
D(XX)=0;%链表起点指向0
k=(i-1)*(a/length+1)+j;
while k~=(X1-1)*(a/length+1)+Y1 %不到终点不停止循环
min=100000;u=0;
for t=1:8
[ti,tj,p]=direct(i,j,t);
if close(ti,tj)==0
if open(ti,tj)==1
if G(ti,tj)>G(i,j)+p
G(ti,tj)=G(i,j)+p;
F(ti,tj)=G(ti,tj)+H(ti,tj);
D((ti-1)*(a/length+1)+tj)=(i-1)*(a/length+1)+j;
end
else
G(ti,tj)=G(i,j)+p;
H(ti,tj)=distance(ti,tj,X1,Y1);
F(ti,tj)=G(ti,tj)+H(ti,tj);
D((ti-1)*(a/length+1)+tj)=(i-1)*(a/length+1)+j;
open(ti,tj)=1;
end
if F(ti,tj)4.4 回溯
通过链表这种数据结构把最短路径通过的节点记录下来,并正向显示路径,代码如下
%回溯将最短路径节点顺序存在jg矩阵中
i=k;
jg=[k];
while D(i)
jg=[i,jg];%存储最短路径通过的节点
i=D(i); %通过链表回溯
end
%填充最短路径为红色
for i=1:size(jg,2)
i1=fix((jg(i)-1)/(a/length+1))+1;%将顺序排列的节点转换为原来的二维坐标
j1=mod(jg(i)-1,(a/length+1))+1;
y=[i1-1,i1-1,i1,i1]*length;
x=[j1-1,j1,j1,j1-1]*length;
h=fill(x,y,'r'); %将最短路径通过的节点填充为红色
pause(0.03);
hold on;
end5 完整版A*算法
5.1 动画
5.2 完整源程序
图像的处理可以修改,起点终点也可以自行调整,动图速度也可以调整。
clc
clear all
set(0,'defaultfigurecolor','w');
Img=imread('C:\Autodesk\WI\ceshi.jpg');
Img = flipud(Img);%y坐标调换,由于读入图像时上下会反转
I = rgb2gray(Img);
a=50;b=50;% 设置网格格数 a表示横轴 b表示纵轴
length=1;%网格边长
B = imresize(I,[a/length b/length]);%对图像进行矩阵化
J=floor(B/(255-30));
%不接近白色的都变为黑色,即变成障碍物,这里的60是可以调整的范围,不同的图像有不同的处理方法
hold on;grid on;%添加网格线
axis([0,a,0,b]);
% gca表示当前绘图区域
% xtick表示x轴坐标刻度,刻度为0到a,步进为1
set(gca,'xtick',0:1:a,'ytick',0:1:b);
set(gca,'xticklabel',[],'yticklabel',[]);
axis image xy
% 障碍物填充为黑色
for i=1:a/length-1
for j=1:b/length-1
if(J(i,j)==0)
y=[i,i,i+1,i+1]*length;
x=[j,j+1,j+1,j]*length;
h=fill(x,y,'k');
hold on
end
end
end
%周围一圈设置成障碍
for i=1:a/length-1
for j=b/length-1:-1:1
J(i,j+1)=J(i,j);
end
end
for i=a/length-1:-1:1
for j=2:b/length
J(i+1,j)=J(i,j);
end
end
j=1;
for i=1:a/length+1
J(i,j)=0;
end
j=a/length+1;
for i=1:a/length+1
J(i,j)=0;
end
i=1;
for j=1:b/length+1
J(i,j)=0;
end
i=b/length+1;
for j=1:b/length+1
J(i,j)=0;
end
i=2;j=2;%起点坐标,注意此时的坐标整体向右上方移动
XX=(i-1)*(a/length+1)+j;%起点行行连接的顺序
X1=47;Y1=6;%终点坐标
%画出起点和终点
y=[j-1,j-1,j,j]*length;
x=[i-1,i,i,i-1]*length;
h=fill(x,y,'y');
hold on;
y=[X1-1,X1,X1,X1-1]*length;
x=[Y1-1,Y1-1,Y1,Y1]*length;
h=fill(x,y,'g');
hold on;
%初始化
open=zeros(a/length+1,a/length+1);
close=1.-J;
close(i,j)=1;
G=zeros(a/length+1,a/length+1);
H=zeros(a/length+1,a/length+1);
F=zeros(a/length+1,a/length+1);
D(XX)=0;%链表起点指向0
k=(i-1)*(a/length+1)+j;
while k~=(X1-1)*(a/length+1)+Y1 %不到终点不停止循环
min=100000;u=0;
for t=1:8
[ti,tj,p]=direct(i,j,t);
if close(ti,tj)==0
if open(ti,tj)==1
if G(ti,tj)>G(i,j)+p
G(ti,tj)=G(i,j)+p;
F(ti,tj)=G(ti,tj)+H(ti,tj);
D((ti-1)*(a/length+1)+tj)=(i-1)*(a/length+1)+j;
end
else
G(ti,tj)=G(i,j)+p;
H(ti,tj)=distance(ti,tj,X1,Y1);
F(ti,tj)=G(ti,tj)+H(ti,tj);
D((ti-1)*(a/length+1)+tj)=(i-1)*(a/length+1)+j;
open(ti,tj)=1;
end
if F(ti,tj)