双目立体匹配（传统/深度）方法总结

总述

部分参考学习OpenCV 3 ¹

---

投影几何

针孔模型：

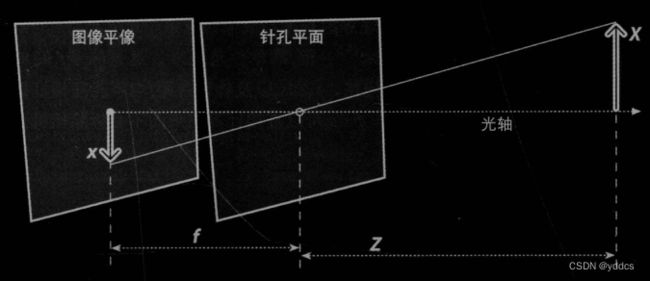
$$-x/f=X/Z$$ 在此作等价转换，将图像平面移至右边----相机o和物体P间，便于表达

而 芯片中心通常不在光轴上，引入两个新的参数$c_x和c_y$， 对投影屏幕中心可能存在的偏移进行建模。

将世界坐标点$P（X，Y，Z）$映射到相机平面上坐标点为 $q(x,y)$ 的过程称为 “ 射影变换 ”，可简单表述为：
$$q=M\cdot P,where$$

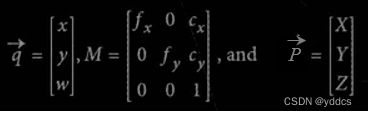
透镜畸变

径向畸变 是由于透镜的形状（筒形）造成的；

切向畸变 是由整个相机的 组装过程 造成的，使透镜与成像平面不平行。

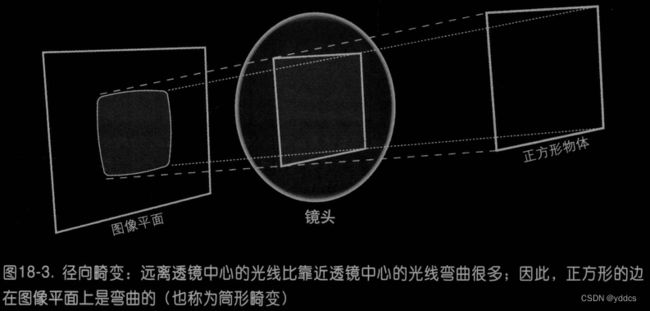
某点的径向位置可用$r=0$附近的泰勒级数展开式的前几项来描述。


共需要求出5个畸变系数，按顺序 $k_1,k_2,p_1,p_2,k_3$

---

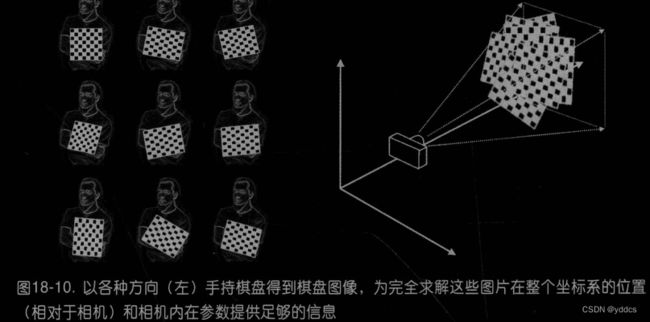
标定

摄像机参数：一般一共15个相关参数：

（1）外参数6个：R 旋转3个参数；T 平移3个参数；

（2）内参数4个：$f_x，f_y，c_x，c_y;$

求解上述10个参数的前提是先假设每次的畸变参数为0；

（3）5个畸变参数：$k_1，k_2，p_1，p_2，k_3；$

其中（2）(3）为摄像机内参数，其中k3普通镜头不使用，鱼眼镜头要使用。

先看 R， T ：

相机拍摄的一个特定物体（世界坐标系），其相对于相机坐标系统的姿态可用 旋转 和 平移 进行描述。

三维旋转可拆解为绕每个轴的二维旋转，如依次绕$x,y,z$轴旋转角度$\phi ，\theta 和\xi$，则总的旋转矩阵R是$R_x(\phi ),R_y(\theta ),R_z(\xi )$三者的乘积。

因此 R 具有其逆矩阵等于其转置矩阵的特性，$R\ast R^T=R^T\cdot R=I_3$。

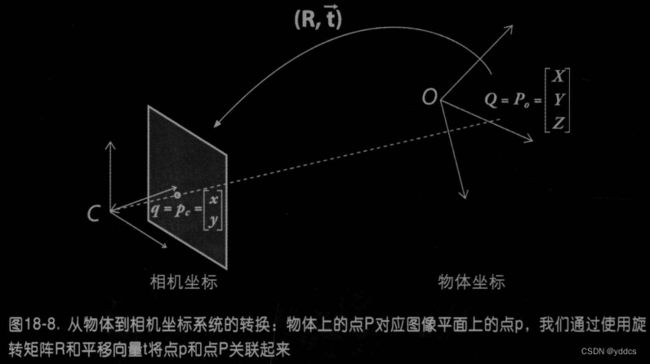
平移向量是以物体中心为原点的坐标系到以相机中心为原点的坐标系的偏移量，因此，相应的平移向量为 $T=origi{n}_{object}-origi{n}_{camera}$,

则，点P在世界坐标系中可表述为 $P_c=R\ast (P_o-T).$

此时

单目标定

1. 找棋盘角点

	vector<Point2f> corners1, corners2;
	bool found_1 = cv::findChessboardCorners(src_1, board_size, corners1);
	bool found_2 = cv::findChessboardCorners(src_2, board_size, corners2);	

2. 进一步精确至亚像素

	Mat gray_img1;
	cv::cvtColor(src_1, gray_img1, cv::COLOR_BGR2GRAY);
	cv::cornerSubPix(gray_img1, corners1,
		Size(5, 5), Size(-1, -1),
		TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 50, 0.1));
	// 存放当前左视图平面角点
	img_pts1.push_back(corners1);
	cout << "correct! " << img_path.c_str() << endl;

3. 绘制棋盘角点

	/* 在图像上显示角点位置*/
	drawChessboardCorners(src_1, board_size, corners1, true); // 用于在图片中标记角点
	imshow("Camera Calibration", src_1);       // 显示图片
	waitKey(500); //暂停0.5S 

本征矩阵 （Essential Matrix）：
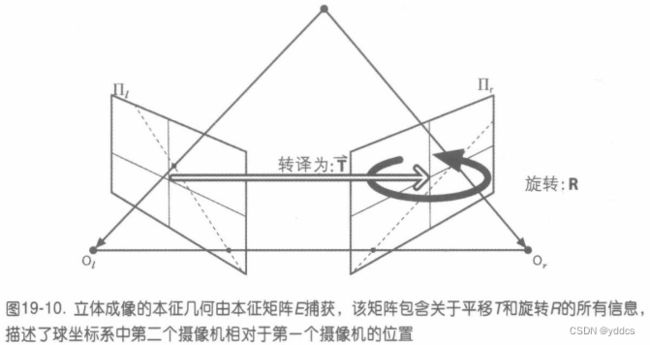基本矩阵（Fundamental Mat）：

双目标定

标定后立体校正的理想状态：

$Fig.2.$ 双目相机测距原理图

焦距$f$, 基线$Baseline(b)$
$$\frac{b}{Z}=\frac{b-(X_R-X_T)}{Z-f}$$ 深度Z，视差$d$
$$Z=\frac{fb}{d},whered=X_R-X_T$$

注意事项：

1. 标定板占图像$1/4-1/3$，标定板距离远近，各种姿态，全图覆盖，剔除误差大的图像对；
2. 确定相机的视差范围（0，$d$）

---

校正

---

立体匹配

传统方法

1 ²

深度学习方法

合理的创建标题，有助于目录的生成

如何改变文本的样式

---

1. 学习OpenCV 3 清华大学出版社 ↩︎

2. mermaid语法说明 ↩︎