动手学强化学习(一)

第 1 章 初探强化学习

1. 强化学习的环境 

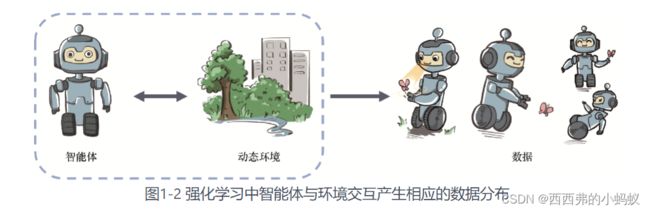
强化学习的智能体是在和一个动态环境的交互中完成序贯决策的。

2. 强化学习的目标

在强化学习中，我们关注回报（return）的期望，并将其定义为价值（value），这就是强化学习中智能体学习的优化目标。

3 强化学习中的数据

在强化学习中，数据是在智能体与环境交互的过程中得到的。如果智能体不采取某个决策动作，那么该动作对应的数据就永远无法被观测到，所以当前智能体的训练数据来自之前智能体的决策结果。因此，智能体的策略不同，与环境交互所产生的数据分布就不同

 

 强化学习则通过改变策略来调整智能体和环境交互数据的分布，进而优化目标，即修改数据分布而目标函数不变。

综上所述，一般有监督学习和强化学习的范式之间的区别为：

• 一般的有监督学习关注寻找一个模型，使其在给定数据分布下得到的损失函数的期望最小；
• 强化学习关注寻找一个智能体策略，使其在与动态环境交互的过程中产生最优的数据分布，即最大化该分布下一个给定奖励函数的期望。

第 2 章 多臂老虎机 

强化学习关注智能体和环境交互过程中的学习，这是一种试错型学习（trial-and-error learning）范式。在正式学习强化学习之前，我们需要先了解多臂老虎机问题，它可以被看作简化版的强化学习问题。与强化学习不同，多臂老虎机不存在状态信息，只有动作和奖励，算是最简单的“和环境交互中的学习”的一种形式。多臂老虎机中的探索与利用（exploration vs. exploitation）问题一直以来都是一个特别经典的问题，理解它能够帮助我们学习强化学习。

多臂老虎机（multi-armed bandit，MAB）问题 

 

2.2.4 估计期望奖励

为了知道拉动哪一根拉杆能获得更高的奖励，我们需要估计拉动这根拉杆的期望奖励。由于只拉动一次拉杆获得的奖励存在随机性，所以需要多次拉动一根拉杆，然后计算得到的多次奖励的期望，其算法流程如下所示。

3)探索与利用的平衡 

探索（exploration）是指尝试拉动更多可能的拉杆，这根拉杆不一定会获得最大的奖励，但这种方案能够摸清楚所有拉杆的获奖情况。例如，对于一个 10 臂老虎机，我们要把所有的拉杆都拉动一下才知道哪根拉杆可能获得最大的奖励。

利用（exploitation）是指拉动已知期望奖励最大的那根拉杆，由于已知的信息仅仅来自有限次的交互观测，所以当前的最优拉杆不一定是全局最优的。 例如，对于一个 10 臂老虎机，我们只拉动过其中 3 根拉杆，接下来就一直拉动这 3 根拉杆中期望奖励最大的那根拉杆，但很有可能期望奖励最大的拉杆在剩下的 7 根当中，即使我们对 10 根拉杆各自都尝试了 20 次，发现 5 号拉杆的经验期望奖励是最高的，但仍然存在着微小的概率—另一根 6 号拉杆的真实期望奖励是比 5 号拉杆更高的。

设计策略时就需要平衡探索和利用的次数，使得累积奖励最大化。一个比较常用的思路是在开始时做比较多的探索，在对每根拉杆都有比较准确的估计后，再进行利用

已有一些比较经典的算法来解决这个问题，例如-贪婪算法、上置信界算法和汤普森采样算法等， 

2.4 ϵ-贪心算法

 

2.6 汤普森采样算法 

 先假设拉动每根拉杆的奖励服从一个特定的概率分布，然后根据拉动每根拉杆的期望奖励来进行选择。但是由于计算所有拉杆的期望奖励的代价比较高，汤普森采样算法使用采样的方式，即根据当前每个动作  的奖励概率分布进行一轮采样，得到一组各根拉杆的奖励样本，再选择样本中奖励最大的动作。可以看出，汤普森采样是一种计算所有拉杆的最高奖励概率的蒙特卡洛采样方法。

第 3 章 马尔可夫决策过程 

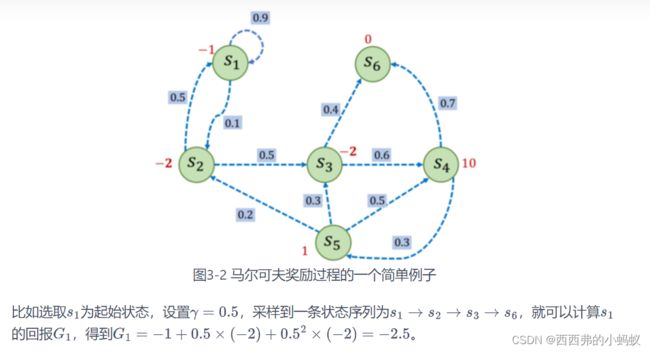
3.2 马尔可夫过程

 

 

 

 3.3.2 价值函数

在马尔可夫奖励过程中，一个状态的期望回报被称为这个状态的价值（value）。所有状态的价值就组成了价值函数（value function），价值函数的输入为某个状态，输出为这个状态的价值。

 

 

 求解较大规模的马尔可夫奖励过程中的价值函数时，可以使用动态规划（dynamic programming）算法、蒙特卡洛方法（Monte-Carlo method）和时序差分（temporal difference），这些方法将在之后的章节介绍

 3.4. 马尔可夫决策过程

如果有一个外界的“刺激”来共同改变这个随机过程，就有了马尔可夫决策过程（Markov decision process，MDP） 

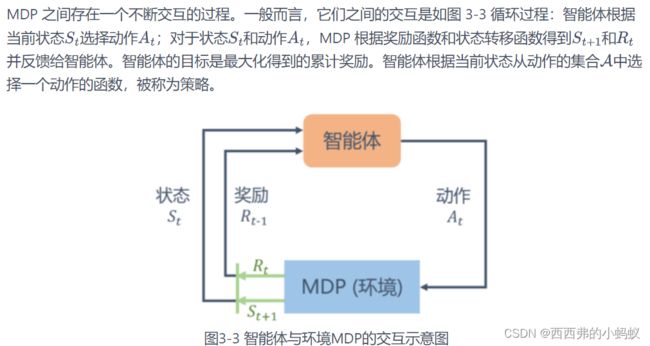
  马尔可夫决策过程是一个与时间相关的不断进行的过程，在智能体和环境 MDP 之间存在一个不断交互的过程。一般而言，它们之间的交互是如图 3-3 循环过程

 3.4.1 策略

智能体的策略（Policy）通常用字母表示。策略是一个函数，表示在输入状态情况下采取动作的概率。因为不同的策略会采取不同的动作，从而之后会遇到不同的状态，以及获得不同的奖励，所以它们的累积奖励的期望也就不同，即状态价值不同。

 

 

 

 于是我们得到了最优状态价值函数和最优动作价值函数之间的关系：

 

第 4 章 动态规划算法

本章介绍如何用动态规划的思想来求解在马尔可夫决策过程中的最优策略。 

基于动态规划的强化学习算法主要有两种：一是策略迭代（policy iteration），二是价值迭代（value iteration）。其中，策略迭代由两部分组成：策略评估（policy evaluation）和策略提升（policy improvement）。具体来说，策略迭代中的策略评估使用贝尔曼期望方程来得到一个策略的状态价值函数，这是一个动态规划的过程；而价值迭代直接使用贝尔曼最优方程来进行动态规划，得到最终的最优状态价值。 

基于动态规划的这两种强化学习算法要求事先知道环境的状态转移函数和奖励函数，也就是需要知道整个马尔可夫决策过程。在这样一个白盒环境中，不需要通过智能体和环境的大量交互来学习，可以直接用动态规划求解状态价值函数。但是，现实中的白盒环境很少，这也是动态规划算法的局限之处，我们无法将其运用到很多实际场景中。另外，策略迭代和价值迭代通常只适用于有限马尔可夫决策过程，即状态空间和动作空间是离散且有限的。

4.3 策略迭代算法

策略迭代是策略评估和策略提升不断循环交替，直至最后得到最优策略的过程。本节分别对这两个过程进行详细介绍。

 4.3.1 策略评估

策略评估这一过程用来计算一个策略的状态价值函数  主要是当前状态的价值

 4.3.2 策略提升

 

 4.4 价值迭代算法

 第 5 章 时序差分算法

不同于动态规划算法，无模型的强化学习算法不需要事先知道环境的奖励函数和状态转移函数，而是直接使用和环境交互的过程中采样到的数据来学习，这使得它可以被应用到一些简单的实际场景中。本章将要讲解无模型的强化学习中的两大经典算法：Sarsa 和 Q-learning，它们都是基于时序差分（temporal difference，TD）的强化学习算法。同时，本章还会引入一组概念：在线策略学习和离线策略学习。通常来说，在线策略学习要求使用在当前策略下采样得到的样本进行学习，一旦策略被更新，当前的样本就被放弃了，就好像在水龙头下用自来水洗手；而离线策略学习使用经验回放池将之前采样得到的样本收集起来再次利用，就好像使用脸盆接水后洗手。因此，离线策略学习往往能够更好地利用历史数据，并具有更小的样本复杂度（算法达到收敛结果需要在环境中采样的样本数量），这使其被更广泛地应用。

5.2 时序差分方法

时序差分是一种用来估计一个策略的价值函数的方法，它结合了蒙特卡洛和动态规划算法的思想。时序差分方法和蒙特卡洛的相似之处在于可以从样本数据中学习，不需要事先知道环境；和动态规划的相似之处在于根据贝尔曼方程的思想，利用后续状态的价值估计来更新当前状态的价值估计

 

 5.3 Sarsa 算法

   1）多步 Sarsa 算法

5.5 Q-learning 算法

 

 

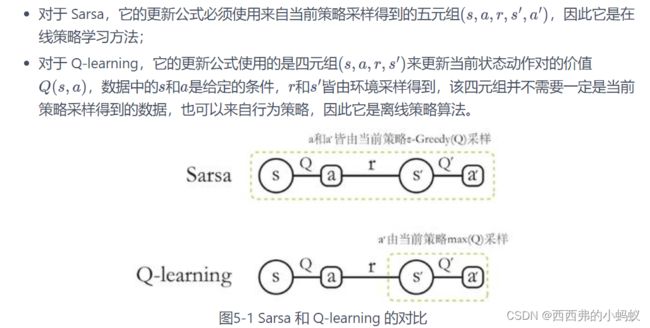
在线策略算法与离线策略算法

我们称采样数据的策略为行为策略（behavior policy），称用这些数据来更新的策略为目标策略

在线策略（on-policy）算法表示行为策略和目标策略是同一个策略；而离线策略（off-policy）算法表示行为策略和目标策略不是同一个策略。Sarsa 是典型的在线策略算法，而 Q-learning 是典型的离线策略算法。判断二者类别的一个重要手段是看计算时序差分的价值目标的数据是否来自当前的策略， 

 

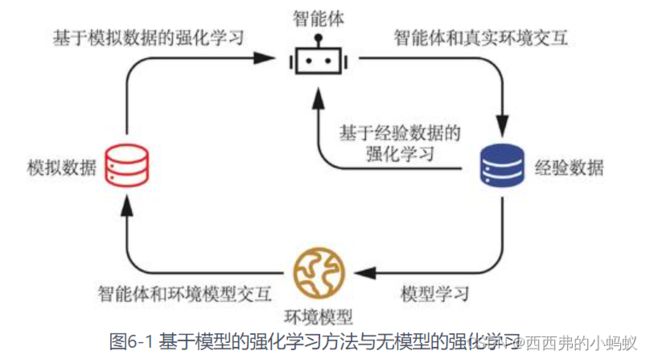
 第 6 章 Dyna-Q 算法

根据是否具有环境模型，强化学习算法分为两种：基于模型的强化学习（model-based reinforcement learning）和无模型的强化学习（model-free reinforcement learning）。

Dyna-Q 算法也是非常基础的基于模型的强化学习算法，不过它的环境模型是通过采样数据估计得到的