(九)学习笔记:动手深度学习(多层感知机 + 代码实现)
目录
- 1. 感知机
-
- 1.1 感知机的基本概念
- 1.2 感知机的训练算法
- 1.3 感知机的收敛定理
- 1.4 感知机的缺陷
- 1.5 感知机总结
- 2. 多层感知机
-
- 2.1 多层感知机的简介
- 2.2 常见激活函数
-
- 2.2.1 ReLU函数
- 2.2.2 sigmoid函数
- tanh函数
- 3. 多层感知机的从零开始实现
-
- 3.1初始化模型参数
- 3.2激活函数
- 3.3模型
- 3.4损失函数
- 3.5训练
- 3.6小结
- 4. 多层感知机的简洁实现
-
- 4.1 模型
- 4.3小结
- 5 答疑
1. 感知机
1.1 感知机的基本概念
1.2 感知机的训练算法
1.3 感知机的收敛定理
1.4 感知机的缺陷
1.5 感知机总结
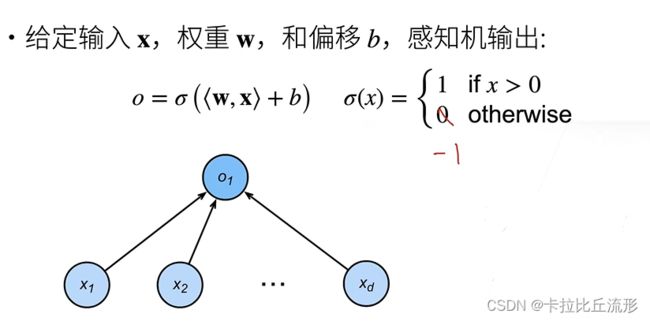
- 感知机是一个二分类模型,是最早的AI模型之一
- 它的求解算法等价于使用批量大小为1的梯度下降
- 它不能拟合XOR函数,导致的第一次AI寒冬
2. 多层感知机
2.1 多层感知机的简介
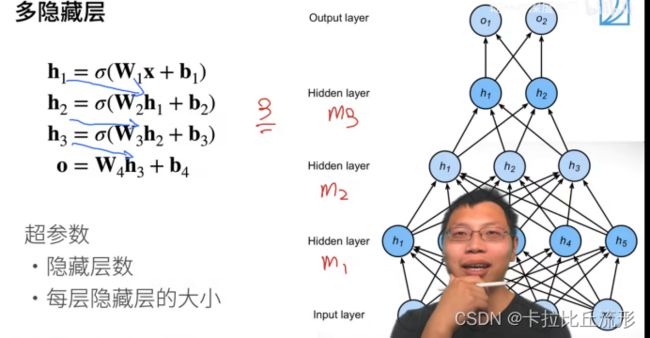
我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制, 使其能处理更普遍的函数关系类型。 要做到这一点,最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层,直到生成最后的输出。 我们可以把前 L − 1 L−1 L−1 层看作表示,把最后一层看作线性预测器。 这种架构通常称为多层感知机(multilayer perceptron),通常缩写为MLP。
多层感知机可以通过隐藏神经元,捕捉到输入之间复杂的相互作用, 这些神经元依赖于每个输入的值。

2.2 常见激活函数
2.2.1 ReLU函数
最受欢迎的激活函数是修正线性单元(Rectified linear unit,ReLU),
因为它实现简单,同时在各种预测任务中表现良好。
[ReLU提供了一种非常简单的非线性变换]。
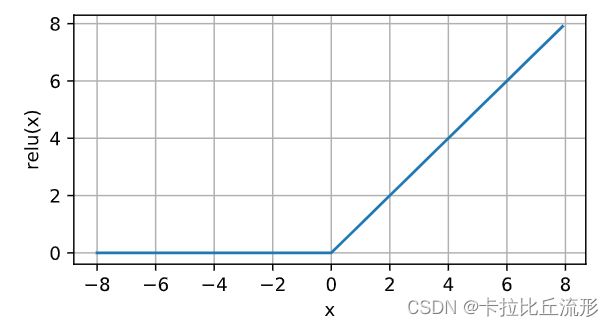
给定元素 x x x,ReLU函数被定义为该元素与 0 0 0的最大值:
ReLU ( x ) = max ( x , 0 ) . \operatorname{ReLU}(x) = \max(x, 0). ReLU(x)=max(x,0).
通俗地说,ReLU函数通过将相应的活性值设为0,仅保留正元素并丢弃所有负元素。
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))
当输入为负时,ReLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。 注意,当输入值精确等于0时,ReLU函数不可导。 在此时,我们默认使用左侧的导数,即当输入为0时导数为0。 我们可以忽略这种情况,因为输入可能永远都不会是0。 这里引用一句古老的谚语,“如果微妙的边界条件很重要,我们很可能是在研究数学而非工程”, 这个观点正好适用于这里。 下面我们绘制ReLU函数的导数。
y.backward(torch.ones_like(x), retain_graph=True)#调用backward时,一定是标量对张量求导
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))

使用ReLU的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过。
这使得优化表现的更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题(稍后将详细介绍)。
注意,ReLU函数有许多变体,包括参数化ReLU(Parameterized ReLU,pReLU)
函数 :cite:He.Zhang.Ren.ea.2015。
该变体为ReLU添加了一个线性项,因此即使参数是负的,某些信息仍然可以通过:
pReLU ( x ) = max ( 0 , x ) + α min ( 0 , x ) . \operatorname{pReLU}(x) = \max(0, x) + \alpha \min(0, x). pReLU(x)=max(0,x)+αmin(0,x).
2.2.2 sigmoid函数
[对于一个定义域在 R \mathbb{R} R中的输入,sigmoid函数将输入变换为区间(0, 1)上的输出]。
因此,sigmoid通常称为挤压函数(squashing function):它将范围(-inf, inf)中的任意输入压缩到区间(0, 1)中的某个值:
sigmoid ( x ) = 1 1 + exp ( − x ) . \operatorname{sigmoid}(x) = \frac{1}{1 + \exp(-x)}. sigmoid(x)=1+exp(−x)1.
在最早的神经网络中,科学家们感兴趣的是对“激发”或“不激发”的生物神经元进行建模。
因此,这一领域的先驱可以一直追溯到人工神经元的发明者麦卡洛克和皮茨,他们专注于阈值单元。
阈值单元在其输入低于某个阈值时取值0,当输入超过阈值时取值1。
当人们的注意力逐渐转移到基于梯度的学习时,sigmoid函数是一个自然的选择,因为它是一个平滑的、可微的阈值单元近似。
当我们想要将输出视作二元分类问题的概率时,sigmoid仍然被广泛用作输出单元上的激活函数(你可以将sigmoid视为softmax的特例)。
然而,sigmoid在隐藏层中已经较少使用,它在大部分时候被更简单、更容易训练的ReLU所取代。
注意,当输入接近0时,sigmoid函数接近线性变换。
y = torch.sigmoid(x)
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))
d d x sigmoid ( x ) = exp ( − x ) ( 1 + exp ( − x ) ) 2 = sigmoid ( x ) ( 1 − sigmoid ( x ) ) . \frac{d}{dx} \operatorname{sigmoid}(x) = \frac{\exp(-x)}{(1 + \exp(-x))^2} = \operatorname{sigmoid}(x)\left(1-\operatorname{sigmoid}(x)\right). dxdsigmoid(x)=(1+exp(−x))2exp(−x)=sigmoid(x)(1−sigmoid(x)).
sigmoid函数的导数图像如下所示。
注意,当输入为0时,sigmoid函数的导数达到最大值0.25;
而输入在任一方向上越远离0点时,导数越接近0。
# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))
tanh函数
[tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上]。
tanh函数的公式如下:
tanh ( x ) = 1 − exp ( − 2 x ) 1 + exp ( − 2 x ) . \operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}. tanh(x)=1+exp(−2x)1−exp(−2x).
注意,当输入在0附近时,tanh函数接近线性变换。
函数的形状类似于sigmoid函数,不同的是tanh函数关于坐标系原点中心对称。
y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))
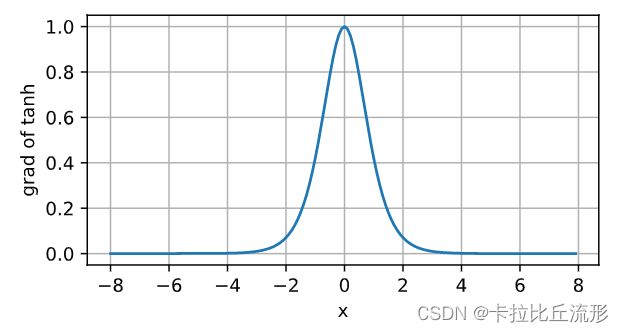
d d x tanh ( x ) = 1 − tanh 2 ( x ) . \frac{d}{dx} \operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x). dxdtanh(x)=1−tanh2(x).
当输入接近0时,tanh函数的导数接近最大值1。
与我们在sigmoid函数图像中看到的类似,输入在任一方向上越远离0点,导数越接近0。
# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))
3. 多层感知机的从零开始实现
为了与之前softmax回归获得的结果进行比较,我们将继续使用Fashion-MNIST图像分类数据集。
import torch
from torch import nn
import d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
3.1初始化模型参数
回想一下,Fashion-MNIST中的每个图像由 28 × 28 = 784 28 \times 28 = 784 28×28=784个灰度像素值组成。所有图像共分为10个类别。
忽略像素之间的空间结构,我们可以将每个图像视为具有784个输入特征和10个类的简单分类数据集。
首先,我们将[实现一个具有单隐藏层的多层感知机,它包含256个隐藏单元]。
注意,我们可以将这两个变量都视为超参数。
通常,我们选择2的若干次幂作为层的宽度。
因为内存在硬件中的分配和寻址方式,这么做往往可以在计算上更高效。
我们用几个张量来表示我们的参数。
注意,对于每一层我们都要记录一个权重矩阵和一个偏置向量。
跟以前一样,我们要为这些参数的损失的梯度分配内存。
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(torch.randn(
num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]
3.2激活函数
为了确保我们对模型的细节了如指掌,我们将[实现ReLU激活函数],而不是直接调用内置的relu函数。
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
3.3模型
因为我们忽略了空间结构,所以我们使用reshape将每个二维图像转换为一个长度为num_inputs的向量。
def net(X):
X = X.reshape((-1, num_inputs))
H = relu(X@W1 + b1) # 这里“@”代表矩阵乘法
return (H@W2 + b2)
3.4损失函数
由于我们已经从零实现过softmax函数( :numref:sec_softmax_scratch),
因此在这里我们直接使用高级API中的内置函数来计算softmax和交叉熵损失。
回想一下我们之前在 :numref:subsec_softmax-implementation-revisited中
对这些复杂问题的讨论。
我们鼓励感兴趣的读者查看损失函数的源代码,以加深对实现细节的了解。
loss = nn.CrossEntropyLoss()
3.5训练
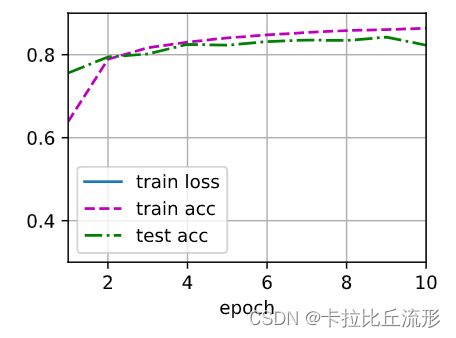
[多层感知机的训练过程与softmax回归的训练过程完全相同]。
可以直接调用d2l包的train_ch3函数,将迭代周期数设置为10,并将学习率设置为0.1.
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)
d2l.predict_ch3(net, test_iter)
3.6小结
- 手动实现一个简单的多层感知机是很容易的。然而如果有大量的层,从零开始实现多层感知机会变得很麻烦(例如,要命名和记录模型的参数)。
4. 多层感知机的简洁实现
(通过高级API更简洁地实现多层感知机)。
import torch
from torch import nn
import d2l
4.1 模型
与softmax回归的简洁实现相比,唯一的区别是我们添加了2个全连接层(之前我们只添加了1个全连接层)。
第一层是[隐藏层],它(包含256个隐藏单元,并使用了ReLU激活函数)。
第二层是输出层。
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
[训练过程]的实现与我们实现softmax回归时完全相同,
这种模块化设计使我们能够将与和模型架构有关的内容独立出来。
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
4.3小结
- 我们可以使用高级API更简洁地实现多层感知机。
- 对于相同的分类问题,多层感知机的实现与softmax回归的实现相同,只是多层感知机的实现里增加了带有激活函数的隐藏层。
5 答疑
- 1.SVM与多层感知机的选择?
SVM的超参数不敏感;mlp可以很容易的改成其它模型,而svm需要修改的东西太多了 - 2.XOR函数的作用?
只是一个反例,一层隐藏层的感知机理论上可以拟合任何函数,但是由于优化算法的局限性无法求解 - 3.为什么神经网络要增加隐藏层的层数,而不是神经元的个数?不是有神经网络万有近似性质吗?
学习一个复杂的东西要从简单的开始学,每一层可以学一个简单的东西 - 4.激活函数的本质?
激活函数的主要作用是完成数据的非线性变换,解决线性模型的表达、分类能力不足的问题