FFT介绍及python源码编写

大纲

1. FFT的来源DFT
2. FFT与DFT的关系
3. FFT的python实现

一、FFT的来源DFT
要了解DFT，就必须要先搞懂DFT，FFT可以看作是为了计算方便而简化之后的DFT，而要了解DFT就需要了解它和DTFT和DFS的关系，关于DTFT和DFS的知识网络上已有许多介绍，不再赘述。
DFT即离散傅立叶变换，它的产生是为了解决DTFT（离散时间傅立叶变换）在频域上连续的问题。众所周知，计算机所能处理的只有离散、有限长的序列，这样就首先排除了我们在信号与系统中所熟知的FS、FT、DFS的应用，但着眼于DFT时我们又发现虽然它在时域上满足离散、有限长的条件，但他在频域上却是连续且周期的，所以我们应当对其在频域上的值进行截断和离散化。这就为我们带来了两个问题：

1.频域采样要满足什么条件，才能使得时域图像不失真？
2.频域采样、截断之后，怎样重构时域信号？

1. 对于频域采样的问题，很容易就联想到奈奎斯特采样定理，二者的原理其实也是一样的，我们通过将带限信号与时域冲激信号相乘进行采样，再对所得频域图像正变换得到周期化（时域离散对应频域周期）之后的频域图像，判断频域图像不混叠的条件从而得到采样定理。频域采样定理同理，我们通过将一个时限信号的频域序列与频域冲激信号相乘进行频域采样，再由卷积定理反变换得到时域图像，发现时域序列进行了周期延拓，判断时域序列不混叠的条件从而得到频域采样定理。

频域取样脉冲S(e^jw)（每2pi内采样N个点，采样频率ws）：

取样后信号频域值：

对频域取样脉冲进行傅立叶级数展开可得：

又通过DFT时移性质和δ ( t )的DFT为1可求得频域脉冲信号离散时间傅立叶反变换：

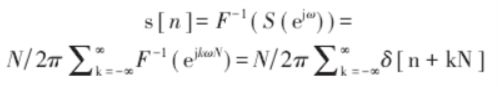
再由卷积定理得频域取样后时域值：

可以发现频域的采样对应的就是时域信号的周期延拓。对于实际运用来说，我们要进行处理的序列都是因果序列（长度为M+1）如下：

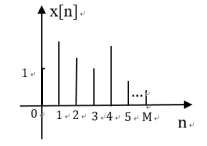
进行周期延拓之后如果N
至此得出了频域采样定理：进行频域采样之后能保证理想重构时域序列的条件是频域采样点数N大于时域序列长度M,由此也就推导出了DFT的正向变换式：

2. 对于还原时域信号的问题，我们要从时域频域对偶特性和DFS入手，当我们对时限信号的频域图像进行采样时，在第一问中就已经知道实际上对时域信号进行了一个周期延拓的操作，即一个域离散、另一个域周期。由此对一个周期序列，我们已知IDFS的公式:

以及DFS的公式:

从而很容易发现这样一个周期序列做DFS之后的值与原信号做DFT之后的值之差一个1/N，所以我们可以用DFT之后的值计算IDFS乘以系数1/N，再对计算结果加矩形窗只取0～M-1个值就得到了原序列。得到IDFT公式如下

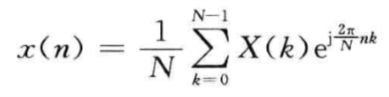
插入：此段可以跳过，为记录时域脉冲FT的一点疑惑

已知冲激函数dalta(t)的傅立叶变换为常数1，那么时域脉冲函数sigma[delta(t-nT),n=(-inf,inf)]由线性性质及时移性质求得FT应该为sigma[exp(-jwnT),n=(-inf,inf)]; 但是如果按照时域脉冲函数的傅立叶级数表示sigma[1/Texp(jnWt),n=(-inf,inf)], 再由1的傅立叶变换为2pisigma(w)和频移特性就求得时域脉冲函数FT为2pi/Tsigma[delta(w-kW),k=(-inf,inf)]. 两个结果在形式上并不相似，那如何让二者统一起来呢？参见下述思路

二、FFT与DFT的关系
首先由将DFT中时间序列取值分为奇、偶两部分得：

而后又有虚指数函数的周期性得：

从而可以将DFT后一半频率的取值与前一半频率的取值联系起来，这样就只需要计算前一半频率对应DFT值，减少了一半的计算量：

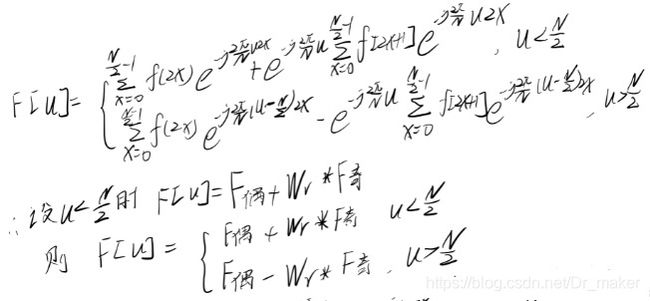
而我们可以发现其实对于每一个F偶和F奇而言，它们都可以视作是对一个新序列（原始序列的奇采样或者偶采样，长度为原来的1/2，u的长度也为原来的1/2）的DFT，他们本身也可以进行上述操作，这样我们就可以递归上述操作，直到最后序列长度为2，此时就可直接使用最原始的公式求之，以长度为16的序列为例（F,Wr的下标表示这一序列应该有多少个值）：

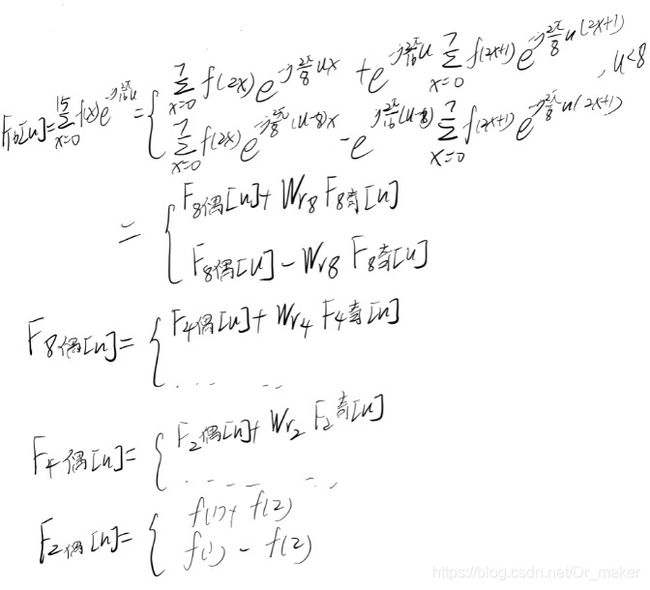
这就是FFT的基本思路了，不断的递归到最后需要计算的实际只有两个频率的值，这样就十分便于计算了。
如果需要计算的是二维DFT，实际上就是按维度先后进行的两个一维DFT：

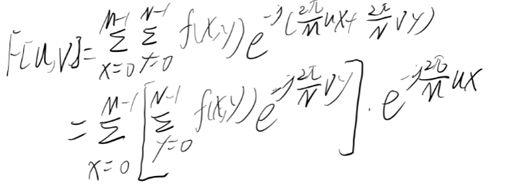
至此，完成了FFT的所有介绍。
三、FFT的python实现

"""
作于2020.08.04 尝试写出二维FFT算法
"""
import numpy as np
import cv2 as cv


def fft_2d(img):
    """
    完成了图片的填，分维度计算FFT
    :param img:输入图片，应该是单通道的灰度图
    :return: FFT之后返回值，复数矩阵
    """
    shape=img.shape
    fft_res = np.zeros(shape,dtype=complex)  # 返回值
    N=2
    while(N<shape[0]):
        N = N<<1  # N二进制左移一位，相当于不断乘2
    num1 = N-shape[0]  # 因为FFT要不断除以2递归，所以要求序列的长度应该是2的幂，用此方法计算出需要补多少个零
    N=2
    while(N<shape[1]):
        N = N<<1
    num2 = N-shape[1]
    # 先对图片第一维（行）进行填充后做一维FFT，再取结果中需要的部分
    fft_res = fft_1d(np.pad(img,((num1//2,num1-num1//2),(0,0)),'edge'),0)[num1//2:num1//2+shape[0],:]
    # 对第二维运算
    fft_res=fft_1d(np.pad(fft_res,((num2//2,num2-num2//2),(0,0)),'edge'),1)[:,num2//2:num2//2+shape[1]]
    return fft_res


def fft_1d(img,axis):
    """
    构造旋转因子矩阵 FFT准备工作
    :param img: 待处理的序列
    :param axis: 判读是第一维还是第二维
    :return: 对某一维FFT之后的序列
    """
    if(axis==0):
        # 构造旋转因子矩阵，由对称性可知，每次计算所需旋转因子个数实际为序列长度的一半，另一半取负号即可
        Wr = np.zeros((img.shape[0]//2,img.shape[1]),dtype=complex)
        temp=np.zeros((1,img.shape[0]//2),dtype=complex)
        for i in range(0,img.shape[0]//2):
            # 计算旋转因子每一列的值
            temp[0][i] = np.cos(2 * np.pi * i / img.shape[0]) - 1j * np.sin(2 * np.pi * i / img.shape[0])
        for i in range(0,img.shape[1]):
            # 因为输入矩阵有不止一列，对行进行FFT时，旋转因子矩阵也有多个相同列
            Wr[:,i]=temp
    elif(axis==1):
        Wr=np.zeros((img.shape[0],img.shape[1]//2),dtype=complex)
        temp=np.zeros(img.shape[1]//2,dtype=complex)  # 因为下面是给每一行赋值temp，所以不能写成*1的二维矩阵，只能用一维，和对列赋值不同
        for i in range(0,img.shape[1]//2):
            temp[i] = np.cos(2*np.pi*i/img.shape[1])-1j*np.sin(2*np.pi*i/img.shape[1])
        for i in range(0,img.shape[0]):
            Wr[i,:]=temp
    else:
        Wr=np.zeros(img.shape)  # 其实没有用，只是不想看到调用Wr时可能为定义就使用
    return fft_calc(img,Wr,axis)

def fft_calc(img,Wr,axis):
    """
    进行FFT最基本的运算及递归，核心部分
    最难理解的部分在于为什么递归时旋转因子矩阵的尺寸在计算维度上不等于原矩阵尺寸，这样如何计算出N个值
    这是因为每次递归由公式可知道每次只需要计算前半部分频率的值（A+Wr*B)，后半部分由对称特性即可求得（A-Wr*B）
    所以每次的A+Wr*B中Wr在计算维度上的尺寸实际上是原图的一半，而递归计算A,B时传入的Wr则是由于分了奇、偶，所以减半
   具体理解参见博客
    :param img: 需要进行FFT计算的矩阵
    :param Wr: 传入的旋转因子
    :param axis: 判断维度
    :return: 矩阵FFT输出值
    """
    # 递归到最后一层，只有两个元素
    pic=np.zeros(img.shape,dtype=complex)
    if img.shape[axis]==2:
        if axis==0:
            pic[0,:]=img[0,:]+Wr*img[1,:]   # 因为最后一层只有两个元素，返回的频率值也就只有两个，由公式就分别是A+B和A-B了
            pic[1,:]=img[0,:]-Wr*img[1,:]
        elif axis==1:
            pic[:,0]=img[:,0]+Wr[:,0]*img[:,1]
            pic[:,1]=img[:,0]-Wr[:,0]*img[:,1]
        return pic
    else:
        if axis==0:
            A=fft_calc(img[::2,:],Wr[::2,:],0)  #计算偶数部分值
            B=fft_calc(img[1::2,:],Wr[::2,:],0)   #计算奇数部分值,这里奇数比偶数多的90度角在后续旋转矩阵中体现，所以奇偶Wr一样
            pic[0:img.shape[0]//2,:]=A+Wr*B   #计算前半频率值
            pic[img.shape[0]//2:img.shape[0],:]=A-Wr*B   #计算后半频率值
        if axis==1:
            A=fft_calc(img[:,::2],Wr[:,::2],1)
            B=fft_calc(img[:,1::2],Wr[:,::2],1)
            pic[:,0:img.shape[1]//2]=A+Wr*B
            pic[:,img.shape[1]//2:img.shape[1]]=A-Wr*B
        return pic



def ifft_2d(img):
    """
    逆FFT，实际上和正变换差别不大，只是旋转因子变号，加了常系数而已
    :param img: 待逆变换的频域图
    :return: 逆FFT后的原图
    """
    shape=img.shape
    N=2
    while(N<shape[0]):
        N=N<<1
    num1=shape[0]-N  #第一维填充量
    N=2
    while(N<shape[1]):
        N=N<<1
    num2=shape[1]-N   #第二维填充量

    ifft_res=ifft_1d(np.pad(img,((num1//2,num1-num1//2),(0,0)),'edge'),0)[num1//2:num1//2+shape[0],:]
    ifft_res=ifft_1d(np.pad(ifft_res,((0,0),(num2//2,num2-num2//2)),'edge'),1)[:,num2//2:num2//2+shape[1]]

    return ifft_res


def ifft_1d(img,axis):
    """
    逆fft的每个维度计算

    :param img: 待计算图
    :param axis: 待计算维度
    :return: 图片某维度逆FFT后的值
    """
    if(axis==0):
        Wr=np.zeros((img.shape[0]//2,img.shape[1]),dtype=complex)
        temp=np.zeros((img.shape[0]//2,),dtype=complex)
        for i in range(0,img.shape[0]//2):
            temp[i]=np.cos(2*np.pi*i/img.shape[0])+1j*np.sin(2*np.pi*i/img.shape[0])
        for i in range(0,img.shape[1]):
            Wr[:,i]=temp
    elif(axis==1):
        Wr=np.zeros((img.shape[0],img.shape[1]//2),dtype=complex)
        temp=np.zeros((img.shape[1]//2,),dtype=complex)
        for i in range(0,img.shape[1]//2):
            temp[i]=np.cos(2*np.pi*i/img.shape[1])+1j*np.sin(2*np.pi*i/img.shape[1])
        for i in range(0,img.shape[1]):
            Wr[i,:]=temp
    else:
        Wr=np.zeros((img.shape[0],img.shape[1]),dtype=complex)
    return fft_calc(img,Wr,axis)*(1.0/img.shape[axis])


if __name__=="__main__":
    img = cv.imread('E://material//assassin.jpeg',0)
    F1 = np.fft.fft2(img[:256, :256])
    F2 = fft_2d(img[:256, :256])
    print((abs(F1 - F2) < 0.0000001).all())
    res1=np.fft.ifft2(F1)
    res2=ifft_2d(F2)
    print((abs(res1-res2)<0.0000001).all())
    cv.namedWindow("source",0)
    cv.namedWindow("fft", 0)
    cv.imshow("source",img[:256,:256])
    cv.imshow("fft",res2.astype(np.uint8))
    cv.waitKey(0)

参考文献
频域采样性质的推导与理解新思路
FFT原理（1p)
FFT代码参考
深入浅出数字信号处理----江志红
DFT的定义
FFT递归介绍