推荐系统模型
实现推荐系统模型,内在思想是协同过滤的思想。即利用大量已有的用户的偏好数据,来估计用户对其未接触过的物品的喜好程度。所以协同过滤思想,实际上就是计算相似度。
计算相似度的常用手段(相关系数,向量之间的夹角余弦,欧式距离)
推荐系统的推荐方式有两种
基于用户的推荐
核心是计算出用户和用户之间的相似度。然后完成推荐
对于基于用户相似性的推荐,用简单的一个词表述,那就是“志趣相投”。事实也是如此。
比如说你想去看一个电影,但是不知道这个电影是否符合你的口味,那怎么办呢?从网上找介绍和看预告短片固然是一个好办法,但是对于电影能否真实符合您的偏好却不能提供更加详细准确的信息。这时最好的办法可能就是这样:
小王:哥们,我想去看看这个电影,你不是看了吗,怎么样?
小张:不怎地,陪女朋友去看的,她看得津津有味,我看了一小半就玩手机去了。小王:那最近有什么好看的电影吗?
小张:你去看《雷霆XX》吧,我看了不错,估计你也喜欢。
小王:好的。
这是一段日常生活中经常发生的对话,也是基于用户的协同过滤算法的基础。
小王和小张是好哥们。作为好哥们,其也应具有相同的爱好。那么在此基础上相互推荐自己喜爱的东西给对方那必然是合乎情理,有理由相信被推荐者也能够较好地享受到被推荐物品所带来的快乐和满足感。
下图展示了基于用户的协同过滤算法的表现形式。
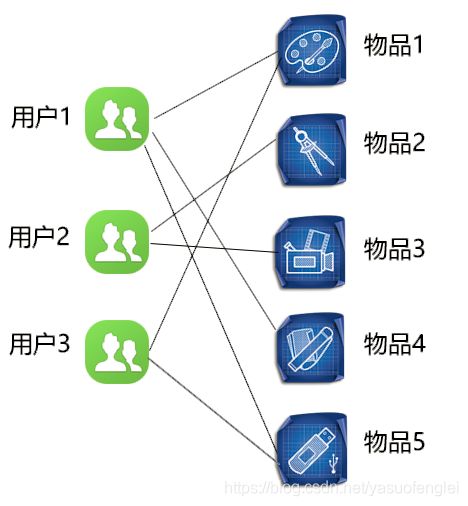
从图上可以看到,想向用户3推荐一个商品,那么如何选择这个商品是一个很大的问题。在已有信息中,用户3已经选择了物品1和物品5,用户2比较偏向于选择物品2和物品4,而用户1选择了物品1、物品4以及物品5。
根据读者的理性思维,不用更多地分析可以看到,用户1和用户3在选择偏好上更加相似。那么完全有理由相信用户1和用户3都选择了相同的物品1和物品5,那么将物品3向用户3推荐也是完全合理的。
这个就是基于用户的协同过滤算法做的推荐。用特定的计算方法扫描和指定目标相同的已有用户,根据给定的相似度对用户进行相似度计算,选择最高得分的用户并根据其已有的信息作为推荐结果从而反馈给用户。这种推荐算法在计算结果上较为简单易懂,具有很高的实践应用价值。
基于物品的推荐
在基于物品的推荐算法中,同样可以使用一个词来形容整个算法的原理。那就是“物以类聚”。
这次小张想给他女朋友买个礼物。
小张:马上情人节快到了,我想给我女朋友买个礼物,但是不知道买什么,上次买了个赛车模型的差点被她骂死。
小王:哦?那你真是的,也不买点她喜欢的东西。她平时喜欢什么啊?
小张:她平时比较喜欢看动画片,特别是《机器猫》,没事就看几集。
小王:那我建议你给她买套机器猫的模型套装,绝对能让她喜欢。
小张:好主意,我试试。
从对话中可以感受到,小张想给自己的女朋友买个礼物从而向小王咨询。
对于不熟悉的用户,在缺少特定用户信息的情况下,根据用户已有的偏好数据去推荐一个未知物品是合理的。这就是基于物品的推荐算法。
生产环境下,建立推荐系统模型,首先需要有:用户-物品矩阵数据
但是生产环境下的用户偏好矩阵往往是稀疏的。
如果直接对稀疏矩阵建模,结果肯定是不准确的,针对空缺数据,不能简单的置为0.我们需要通过某种算法,将空缺数据预测出来。然后计算相似度
- 举个简单的例子,假设我们有如下用户对电影的评级数据:
Tom, Star Wars, 5
Jane, Titanic, 4
Bill, Batman, 3
Jane, Star Wars, 2
Bill, Titanic, 3
它们可转为如下评级矩阵:

为了更好的实现推荐系统,我们需要对这个稀疏的矩阵建模。一般可以采用矩阵分解(或矩阵补全)的方式。
具体就是找出两个低维度的矩阵,使得它们的乘积是原始的矩阵。因此这也是一种降维技术。假设我们的用户和物品数目分别是U和I,那对应的“用户-物品”矩阵的维度为U×I,如下图所示:
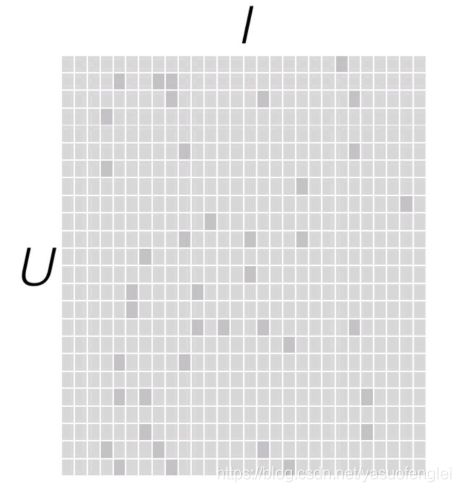
要找到和“用户-物品”矩阵近似的k维(低阶)矩阵,最终要求出如下两个矩阵:一个用于表示用户的U×k维矩阵,以及一个表征物品的k×I维矩阵。这两个矩阵也称作因子矩阵。它们的乘积便是原始评级矩阵的一个近似。值得注意的是,原始评级矩阵通常很稀疏,但因子矩阵却是稠密的(满秩的),如下图所示:
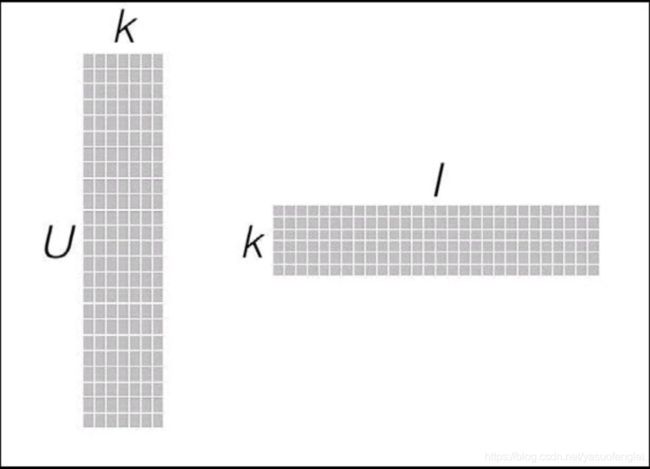
这类模型试图发现对应“用户-物品”矩阵内在行为结构的隐含特征(这里表示为因子矩阵),所以也把它们称为隐特征模型。隐含特征或因子不能直接解释,但它可能表示了某些含义,比如对电影的某个导演、种类、风格或某些演员的偏好。
由于是对“用户-物品”矩阵直接建模,用这些模型进行预测也相对直接:要计算给定用户对某个物品的预计评级,就从用户因子矩阵和物品因子矩阵分别选取相应的行(用户因子向量)与列(物品因子向量),然后计算两者的点积即可。如下图所示:
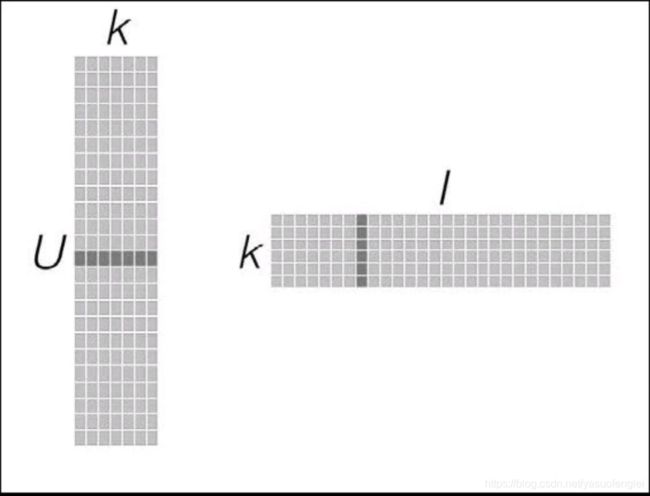
而对于物品之间相似度的计算,可以用最近邻模型中用到的相似度衡量方法。不同的是,这里可以直接利用物品因子向量,将相似度计算转换为对两物品因子向量之间相似度的计算,如下图所示:

因子分解类模型的好处在于,一旦建立了模型,对推荐的求解便相对容易。所以这类模型的表现通常都很出色。但弊端可能在于因子数量的选择有一定困难,往往要结合具体业务和数据量来决定。一般来说,因子的取值范围在10~200之间。
ALS算法原理概述

过拟合的概念:
在训练模型时,目标是使得模型的误差最小,即误差越小,模型拟合得越好。但有些时候,拟合得太好,就会造成过拟合。过拟合的结果:模型在实验环境下很准,但是一放到生产环境下就不准了,这种情况就是过拟合。
ALS是交替最小二乘(alternating least squares)的简称。在机器学习中,ALS特指使用交替最小二乘求解的一个协同推荐算法。它通过观察到的所有用户给商品的打分,来推断每个用户的喜好并向用户推荐适合的商品。比如下图:

这个矩阵的每一行代表一个用户(u1,u2,u3)、每一列代表一个商品(v1,v2,v3)、用户的打分为1-5分。这个矩阵只显示了观察到的打分,我们需要推测没有观察到的打分。比如(u1,v3)打分多少?如果以数独的方式来解决这个问题,可以得到唯一的结果。 因为数独的规则很强,每添加一条规则,就让整个系统的自由度下降一个量级。当我们满足所有的规则时,整个系统的自由度就降为1了,也就得出了唯一的结果。对于上面的打分矩阵,如果我们不添加任何条件的话,也即打分之间是相互独立的,我们就没法得到(u1,v3)的打分。 所以在这个用户打分矩阵的基础上,我们需要提出一个限制其自由度的合理假设,使得我们可以通过观察已有打分来猜测未知打分。
ALS的核心就是这样一个假设:打分矩阵是近似低秩的。换句话说,就是一个UI的打分矩阵可以由分解的两个小矩阵U(Uk)和I(k*I)的乘积来近似。这就是ALS的矩阵分解方法。
ALS算法原理实现思想
.
如何算得因子矩阵里的因子数值是ALS算法要解决的问题,这需要一个明确的可量化目标,ALS用每个元素重构误差的平方和来进行量化。
因为在原评级矩阵中,大量未知元是我们想推断的,所以这个重构误差是包含未知数的。 而ALS算法的解决方案很简单:只计算已知打分的重构误差。
ALS的实现原理是迭代式求解一系列最小二乘回归问题。在每一次迭代时,固定用户因子矩阵或是物品因子矩阵中的一个,然后用固定的这个矩阵以及评级数据来更新另一个矩阵。之后,被更新的矩阵被固定住,再更新另外一个矩阵。如此迭代,直到模型收敛(或是迭代了预设好的次数)。
所以在MLlib的ALS算法中,首先对U或者I矩阵随机化生成,在每一次迭代时,固定用户因子矩阵或是物品因子矩阵中的一个,然后用固定的这个矩阵以及评级数据来更新另一个矩阵,然后利用被求取的矩阵对象去求随机化矩阵。最后两个对象相互迭代计算,直到模型收敛。
ASL算法推导

Spark的Mlib里的协同过滤引用了ALS算法的核心论文,具体可参见:
http://spark.apache.org/docs/latest/mllib-collaborative-filtering.html
Collaborative Filtering - RDD-based API
• Collaborative filtering
• Explicit vs. implicit feedback
• Scaling of the regularization parameter
• Examples
• Tutorial
Collaborative filtering
Collaborative filtering is commonly used for recommender systems. These techniques aim to fill in the missing entries of a user-item association matrix. spark.mllib currently supports model-based collaborative filtering, in which users and products are described by a small set of latent factors that can be used to predict missing entries. spark.mllib uses the alternating least squares (ALS) algorithm to learn these latent factors. The implementation in spark.mllib has the following parameters:
• numBlocks is the number of blocks used to parallelize computation (set to -1 to auto-configure).
• rank is the number of features to use (also referred to as the number of latent factors).
• iterations is the number o alpha is a parameter applicable to the implicit feedback variant of ALS that governs the baseline confidence in preference observations.
过拟合(Overfitting)
当收集到样本数据之后,我们会建立目标方程拟合样本数据。一般的,我们希望模型能尽可能的支拟合样本。但如果所拟合的过好,就会产生生过拟合现象。
如果产生过拟合,会导致 :模型在实验环境表现良好,但是模型在生产环境表现很差,失去实用价值。
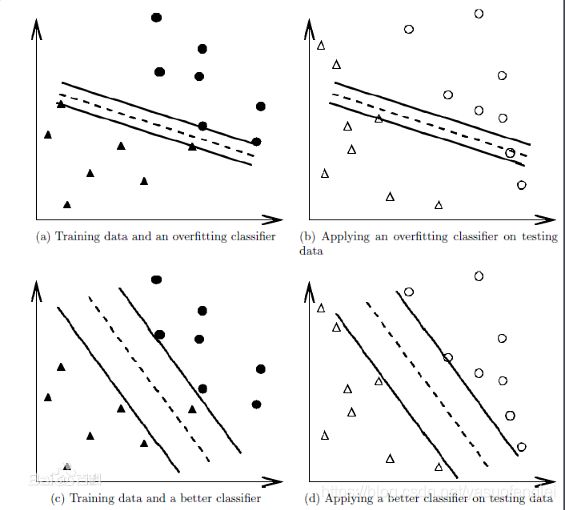
可以看出在a中虽然完全的拟合了样本数据,但对于b中的测试数据分类准确度很差。而c虽然没有完全拟合样本数据,但在d中对于测试数据的分类准确度却很高。过拟合问题往往是由于训练数据少等原因造成的。
解决过拟合的手段
- 引入正则化参数
- 更换模型,比如集成模式(比如 )
模型存储与加载
模型存储
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.spark.mllib.recommendation.Rating
import org.apache.spark.mllib.recommendation.ALS
object Driver2 {
def main(args: Array[String]): Unit = {
val conf=new SparkConf().setMaster("local").setAppName("movie")
val sc=new SparkContext(conf)
val data=sc.textFile("d://ml/u.data")
val movieData=sc.textFile("d://ml/u.item")
val ratings=data.map { line =>{
val infos=line.split("\t")
val userId=infos(0).toInt
val movieId=infos(1).toInt
val score=infos(2).toDouble
Rating(userId,movieId,score)
} }
val model=ALS.train(ratings,50,10,0.01)
model.save(sc, "d://ml/")
}
}
模型加载
import org.apache.spark.SparkContext
import org.apache.spark.SparkConf
import org.apache.spark.mllib.recommendation.ALS
import org.apache.spark.sql.SQLContext
import org.apache.spark.mllib.recommendation.MatrixFactorizationModel
object Driver3 {
def main(args: Array[String]): Unit = {
val conf=new SparkConf().setMaster("local").setAppName("movie")
val sc=new SparkContext(conf)
val model=MatrixFactorizationModel.load(sc,"d://ml/")
val result=model.recommendProducts(789,10)
result.foreach{println}
}
}
实现物品推荐
推荐系统的推荐方式有两种
- 基于用户的推荐:Spark的ALS模型只提供了基于用户的推荐
- 基于物品的推荐:比如某个用户看过了123号这部电影,然后要求推荐123电影相关的电影
这种基于物品的推荐物品的方式,需要程序员自己实现(Spark的ALS模型没有提供)
实现思路
//1. 核心的需求 要计算出物品和物品的相似度。由此引出:需要获取物品因子矩阵
//获取用户的因子矩阵
val userFactors=model.userFeatures
//获取物品的因子矩阵(主要用这个)
//RDD[(itemId,item的因子数组)]
val itemFactors=model.productFeatures
//2比如我们想基于123号这部电影做推荐
//所以先获取123号这部电影的因子值
//下面的代码表示以电影id属性为key,具体找123号的数据
val movie123Factor=itemFactors.keyBy{x=> x._1}.lookup(123).head._2
//基于123号电影推荐10部电影
//计算出其它电影和123号电影的相似度(向量之间的夹角余弦来计算)
//然后按相似度做降序排序,取出前10部推荐。
val result=itemFactors.map{case(movieId,factor)=>
//factor和movie123Factor的余弦距离
val cos=cosArray(movie123Factor,factor)
//返回(当前电影id,与123号电影的夹角余弦)
(movieId,cos)
}
val movie123Top10=result.sortBy{x=>x._2}.take(11).drop(1)
def cosArray(a1:Array[Double],a2:Array[Double])={
val a1a2=a1 zip a2
val a1a2Fenzi=a1a2.map{x=>x._1*x._2}.sum
val a1Fenmu=Math.sqrt(a1.map{x=>x*x}.sum)
val a2Fenmu=Math.sqrt(a2.map{x=>x*x}.sum)
val a1a2Cos=a1a2Fen/(a1Fenmu*a2Fenmu)
a1a2Cos
}
推荐系统的冷启动问题
指建立推荐系统时,缺少用户偏好数据,或者对于一个新用户而言(此时后台数据中并没有此用户的偏好数据),对于出现的这种问题,称为推荐系统的冷启动。
如何解决?
- 解决方案1
新用户在注册时,根据选择的感兴趣方向做相关内容的推荐 - 解决方案2
根据用户的注册信息,做推荐 - 解决方案3
根据热搜排行榜推荐 - 解决方案4
根据用户浏览的商品,加入购物车的商品,购买的商品做物品推荐。
物品冷启动
当一个新的商品上架,一般都会在主页上推荐此商品,目的是让更多的用户浏览和购买此商品,从而积累商品的评分数据。
此外,对于一个新商品,最初可人为打分。最初的是不准的。但是随着打分(使用)的人数增多,评分会趋近于真实值。
系统冷启动
首要解决数据源问题
- 通过爬虫技术爬取数据
- 通过数据网站购买数据
- 自身平台的运营积累