手写体识别实现

手写体识别

简要介绍

深度学习的整个网络中包含输入和输出，可以通过调整参数减少输出数据与正确答案之间的误差的方式进行学习。依次编程实现输入数据和正确答案数据的准备、各个网络层的封装类、正向传播和反向传播的函数。

在完成每轮epoch后，对误差进行测算并显示。此外，将误差随epoch训练次数变化情况和准确率用plt进行可视化。

深度神经网络实现：在神经网络中包括输入层、中间层、输出层。输入层负责接受网络中所有的输入，输出层负责对神经网络进行整体的输出。中间层是介于输入层和输出层之间的多个网络层。在这些网络层中，只有中间层和输出层负责进行神经元的运算，输入层只负责将其接受到的输入信息传递给中间层。

正向传播部分负责传递输入信息到产生输出过程；

反向传播部分负责从输出向输入逆向传递信息。在反向传播中，是使用梯度下降算法决定修正量的大小的。要对神经网络中的所有权重和偏置进行更新，首先要做的就是对所有的权重和偏置计算其所对应误差的梯度。在计算得到全部的梯度后，就要根据公式对所有的权重和偏置进行更新处理。

不论是用pytorch还是原生python实现深度网络都需要对模型进行建立。

1. 环境的搭建（使用pytorch时环境配置更加复杂，使用conda可以方便快捷配置；原生代码则仅设计几个库的调用）

2. 读取并显示手写数字数据集（pytorch实现时，使用MNIST数据集；原生代码实现时使用sklearn的load_digits数据集）

MNIST数据

  > digits数据

3. 数据的预处理

4. 输入层、中间层、输出层的编程实现（pytorch有方便的调用方法）

5. 模型训练

6. 评价指标可视化

pytorch实现

代码实现

import torch
import torchvision
import numpy as np
import matplotlib.pyplot as plt
# 导入pytorch内置的mnist数据
from torchvision.datasets import mnist
# 导入预处理模块
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
# 导入nn及优化器
import torch.nn.functional as F
import torch.optim as optim
from torch import nn

n_epochs = 3
batch_size_train = 64
batch_size_test = 1000
learning_rate = 0.01
momentum = 0.5
log_interval = 100
random_seed = 1
torch.manual_seed(random_seed)

# 定义与处理函数，这些预处理依次放在compose函数中
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize([0.5], [0.5])])
# 下载数据，并对数据进行预处理
train_dataset = mnist.MNIST('./data', train=True, transform=transform)
test_dataset = mnist.MNIST('./data', train=False, transform=transform)
# dataloader是一个可迭代对象，可以使用迭代器一样使用
train_loader = DataLoader(train_dataset, batch_size=batch_size_train, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size_test, shuffle=False)


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
        self.conv2_drop = nn.Dropout2d()
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)
    def forward(self, x):
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
        x = x.view(-1, 320)
        x = F.relu(self.fc1(x))
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)
        return F.log_softmax(x)

network = Net()
optimizer = optim.SGD(network.parameters(), lr=learning_rate,momentum=momentum)
train_losses = []
train_counter = []
test_losses = []
test_counter = [i*len(train_loader.dataset) for i in range(n_epochs + 1)]

def train(epoch):
  network.train()
  for batch_idx, (data, target) in enumerate(train_loader):
    optimizer.zero_grad()
    output = network(data)
    loss = F.nll_loss(output, target)
    loss.backward()
    optimizer.step()
    if batch_idx % log_interval == 0:
      print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
        epoch, batch_idx * len(data), len(train_loader.dataset),
        100. * batch_idx / len(train_loader), loss.item()))
      train_losses.append(loss.item())
      train_counter.append(
        (batch_idx*64) + ((epoch-1)*len(train_loader.dataset)))
      torch.save(network.state_dict(), './model.pth')
      torch.save(optimizer.state_dict(), './optimizer.pth')
          
def test():
  network.eval()
  test_loss = 0
  correct = 0
  with torch.no_grad():
    for data, target in test_loader:
      output = network(data)
      test_loss += F.nll_loss(output, target, size_average=False).item()
      pred = output.data.max(1, keepdim=True)[1]
      correct += pred.eq(target.data.view_as(pred)).sum()
  test_loss /= len(test_loader.dataset)
  test_losses.append(test_loss)
  print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
    test_loss, correct, len(test_loader.dataset),
    100. * correct / len(test_loader.dataset)))
    
for epoch in range(1, n_epochs + 1):
  train(epoch)
  test()
import matplotlib.pyplot as plt
fig = plt.figure()
plt.plot(train_counter, train_losses, color='blue')
plt.scatter(test_counter, test_losses, color='red')
plt.legend(['Train Loss', 'Test Loss'], loc='upper right')
plt.xlabel('number of training examples seen')
plt.ylabel('negative log likelihood loss')
plt.show()

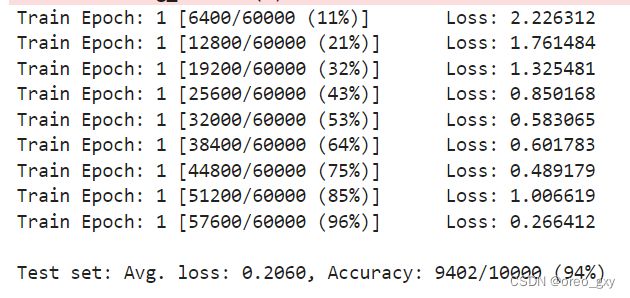
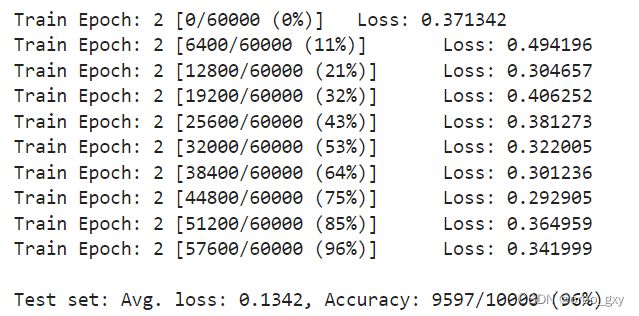
运行结果

误差随训练过程减少

python实现（不用框架）

代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
# 设置各项参数
img_size = 8  # 图像的高度和宽度
n_mid = 16  # 中间层的神经元数量
n_out = 10
eta = 0.001  # 学习系数
epochs = 51
batch_size = 32
interval = 5  # 显示处理进度的时间间隔

digits_data = datasets.load_digits()
# --输入数据--
input_data = np.asarray(digits_data.data)
# 平均值为0、标准差为1
input_data =(input_data - np.average(input_data))/np.std(input_data)
# 正确答案数据
correct = np.asarray(digits_data.target)
correct_data=np.zeros((len(correct),n_out))
# print("aaa",correct.shape)
for i in range(len(correct)):
    correct_data[i,correct[i]]=1
# 分割为测试集和训练集
x_train,x_test,t_train,t_test=train_test_split(input_data,correct_data)


# 全连接层的父类
class BaseLayer:
    def update(self,eta):
        self.w -=eta*self.grad_w
        self.b -=eta*self.grad_b


# 中间层
class MiddleLayer(BaseLayer):
    def __init__(self,n_upper,n):
        # He的初始值
        # print("n_upper&n:",n_upper,n)
        self.w=np.random.randn(n_upper,n)*np.sqrt(2/n_upper)
        self.b=np.zeros(n)

    def forward(self,x):
        self.x=x#x来自x_mb
        self.u=np.dot(x,self.w)+self.b
        # print("self.u1:",x.shape[0],x.shape[1],"*",self.w.shape[0],self.w.shape[1],"=",self.u.shape[0],self.u.shape[1])
        self.y=np.where(self.u<=0,0,self.u) #ReLu

    def backward(self,grad_y):
        # print("self.u2:", self.u.shape[0],self.u.shape[1])
        # print("grad_y:", grad_y.shape[0],grad_y.shape[1])
        # print("np_where:", np.where(self.u<0,0,1).shape[0],np.where(self.u<0,0,1).shape[1])
        delta = grad_y*np.where(self.u<=0,0,1)#ReLu的微分

        self.grad_w = np.dot(self.x.T,delta)
        self.grad_b = np.sum(delta,axis=0)
        self.grad_x = np.dot(delta,self.w.T)#32 10*10 64


# 输出层
class OutputLayer(BaseLayer):
    def __init__(self,n_upper,n):
        # Xavier的初始值
        self.w = np.random.randn(n_upper,n)/np.sqrt(n_upper)
        self.b = np.zeros(n)

    def forward(self,x):
        self.x = x
        u = np.dot(x,self.w)+self.b
        #Softmax函数
        self.y = np.exp(u)/np.sum(np.exp(u),axis=1,keepdims=True)

    def backward(self,t):
        delta = self.y-t

        self.grad_w = np.dot(self.x.T,delta)
        self.grad_b = np.sum(delta,axis=0)
        self.grad_x = np.dot(delta,self.w.T)
# print("img_size&n_mid", img_size , n_mid)


# 各个网络层的初始化
layers = [MiddleLayer(img_size*img_size,n_mid), MiddleLayer(n_mid,n_mid), OutputLayer(n_mid,n_out)]


# 正向传播
def forward_propagation(x):
    for layer in layers:
        layer.forward(x)
        x = layer.y
    return x


# 反向传播
def backpropagation(t):
    grad_y=t
    for layer in reversed(layers):
        layer.backward(grad_y)
        grad_y=layer.grad_x
    return grad_y


# 参数的更新
def update_params():
    for layer in layers:
        layer.update(eta)


# 误差的测定
def get_error(x, t):
    y = forward_propagation(x)
    return -np.sum(t*np.log(y+1e-7))/len(y)  # 交叉熵误差


# 准确率的测定
def get_accuracy(x, t):
    y = forward_propagation(x)
    count = np.sum(np.argmax(y, axis=1) == np.argmax(t, axis=1))
    return count/len(y)


# 误差记录
error_record_train = []
error_record_test = []

n_batch = len(x_train)# 每轮epoch的批次大小,batch_size
for i in range(epochs):
    # 学习
    index_random = np.arange(len(x_train))
    np.random.shuffle(index_random)# 打乱索引顺序
    for j in range(n_batch):
        # 提取小批次数据
        mb_index = index_random[j*batch_size:(j+1)*batch_size]
        # print("t_train:",t_train.shape[0],t_train.shape[1])
        x_mb = x_train[mb_index, :]
        t_mb = t_train[mb_index, :]
        # print("t_mb:",t_mb.shape[0],t_mb.shape[1])
        # 正向传播和反向传播
        forward_propagation(x_mb)
        backpropagation(t_mb)

        # 参数的更新
        update_params()
    # 误差的测量和记录
    error_train = get_error(x_train, t_train)
    error_record_train.append(error_train)
    error_test = get_error(x_test, t_test)
    error_record_test.append(error_test)
    # 显示处理的进度
    if i % interval == 0:
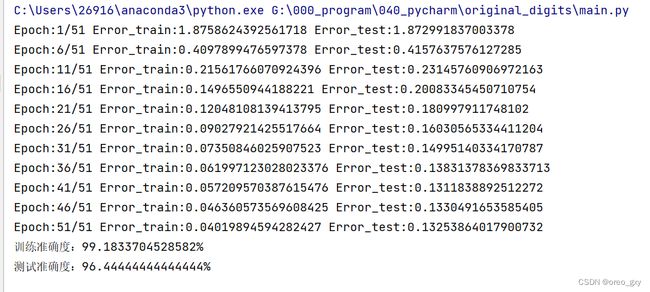
        print("Epoch:"+str(i+1)+"/"+str(epochs), "Error_train:"+str(error_train), "Error_test:"+str(error_test))
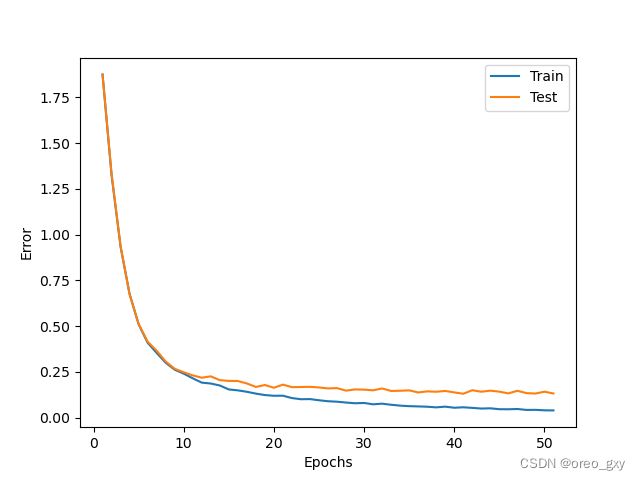
# 用图表显示误差的推移
plt.plot(range(1, len(error_record_train)+1), error_record_train, label="Train")
plt.plot(range(1, len(error_record_test)+1), error_record_test, label="Test")
plt.legend()

plt.xlabel("Epochs")
plt.ylabel("Error")
plt.show()
# 准确率的测定
acc_train = get_accuracy(x_train, t_train)
acc_test = get_accuracy(x_test, t_test)
print("训练准确度："+str(acc_train*100)+"%\n测试准确度："+str(acc_test*100)+"%")

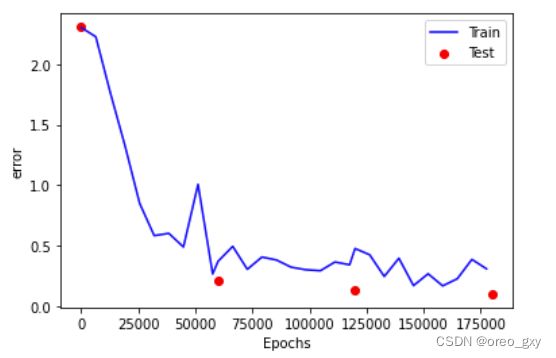
运行结果

误差的变化与准确率

从结果可以看出，训练数据和测试用数据的误差都呈现平滑下降的趋势。由于随机数的影响，虽然每次执行代码后的结果多少有点变动，但是基本上可以达到95%以上的准确率