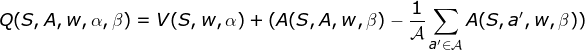【RL】DQN及其各种优化算法
博主的github链接,欢迎大家来访问~:https://github.com/Sh-Zh-7
强化学习经典算法实现地址:https://github.com/Sh-Zh-7/reinforce-learning-impl
上一篇博文的末尾,我们介绍了传统QLearning的劣势——那就是需要维护一个Q表,而对于很多状态,连续动作的情况,我们Q表的大小将会爆炸性地增长。我们微小的内存必然存不下这么大的Q表。所以我们要转换我们的思路。
其实,Q表在之前的QLearning中,只是扮演了一个函数的角色——这句话怎么理解?给定动作和状态,他会给你返回一个价值。
所以我们为什么不直接建立一个函数呢? 这样我们既可以完成Q表的任务,而且也不用爆内存。可选的函数有:线性函数,决策树,最近邻,傅里叶变换,神经网络等。神经网络作为一个universal approximator,自然成了我们的首选,使用神经网络作为函数的Qlearning,就叫Deep Q-Learning(DQN)。
1. DQN原理
既然我们要使用神经网络,那你总要指定输入和输出吧。这里我们的输入和输出总共有两种:
- 给定状态和动作,输出对应的Q值,这个其实挺少用的。优点就是对于连续的动作依然能够建模。
- 还有一种是给定状态,输出所用动作的Q值。显然这种情况就不能对连续的动作建模了。
知道输入输出以后我们还得知道我们的优化目标。其实我们的优化目标和我们的QLearning一样:
我们有:
我们希望我们的估计值和真实的Q值越接近越好,因此我们的residual也出来了。
本质上,这就是一个Regression问题。
2. ReplayBuffer
在做DQN的时候,我们需要引入一个experience replay的概念
采用replay buffer的好处是:
- 可以使用之前的数据进行训练,减少了与环境互动的次数。
-
使用当前的policy采集训练数据,可能会采不到很多(s, a)的reward,即使这些(s, a)是过去曾经访问过的。所以当前这些采不到的地方就没有training signal,因此Q-network在这些(s, a) pair上的预测就不会继续改进。由于网络的capacity 有限,反复拟合当前policy的数据,甚至会扭曲这些曾经访问过的(s, a) pair的Q预测值
3. DQN流程
其实DQN的流程和QLearning的流程差不太多。关键就在于一个参数的更新:
4. DQN的改进
考虑到未来这些paper里面各种新颖的名次都会被当作DQN的一个简单改进技术,我就不花时间介绍他们了。
(1)NatureDQN——使用target network来更新Q值
这里我们使用了两个网络,一个叫做当前网络,另一个叫做目标网络。之所以会使用两个网络,是因为之前用一个网络的时候,同一个状态和动作,你的结果其实是不断变动的,这就会造成我们训练的困难。
最好的情况就是,我们能过固定住其中的一个网络,这样我们的结果也就固定了——当然两个网络之间不能差太多,所以要每隔一段时间更新网络参数。
用数学公式写就是:
(2)DoubleDQN——解耦目标Q值动作的选择和目标Q值的计算
实验表明,我们用神经网络拟合出来的Q值,其实是比真实值要估得高的。这是由于使用了贪婪法计算Q值,使Q值的计算可能过早的向一个早期计算出的局部的最优Q值靠拢,导致出现大的偏差。导致其他较优的局部状态动作无法被迭代到,或者就算迭代到,也没有更新到高的Q值。这样偏差就大了。
一个解决办法就是,利用贪婪法+当前网络选择相应的动作。
(3)PrioritizedReplayDQN——对于具有较高价值的样本进行优先的计算
之前我们ReplayBuffer对待所有样本都一视同仁。实际也是如此吗?当然不是。
比如,具有较大误差的样本,就具有更高的价值,采样的时候,可以利用这个增加较大误差样本被采样到的几率,来实现这个操作。
实现的方法是利用一个SumTree的数据结构(其实使用list也行,但是效率低,一个是O(n), 另一个是O(logn))
核心思想是把权重转化为区间,你叶子节点的值就是对应区间的长度。显然权重越大,落到这个区间的概率也就越大。
这颗SumTree是专门用来存取优先级的,为此你还要有一个list用来存储transiton。
(P.S. 特别注意0的存在!!真的很要命!!)
上图终,叶子节点就是区间长度,其父节点的值是叶子节点值的和。
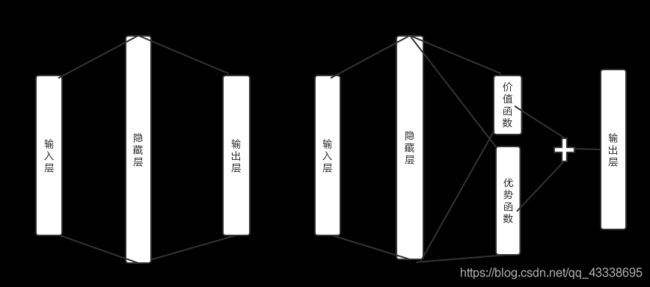
(4) DuelingDQN——改善网络结构
这个更简单,事实上你只要知道他是更改网络结构就对了。他主要是在网络的内部又细分了:
它所细分的,就是分成了一个价值函数层和优势函数层,最后又将他们线性组合。
注意,优势函数层还要中心化,最后的数学公式如下:
这样做得目的是更有效率地进行训练。比如某一状态所有的动作的价值,都要+1。那我们就没必要去对于每一个s a对进行更新,只要更新一个V就行了。见下图所示: