KNN 最近邻算法(K近邻)
机器学习教程 正在计划编写中,欢迎大家加微信 sinbam 提供意见、建议、纠错、催更。
KNN(K-Nearest Neighbor)是机器学习入门级的分类算法,也是最为简单的算法。它实现将距离近的样本点划为同一类别,KNN 中的K指的是近邻个数,也就是最近的K个点,根据它距离最近的K个点是什么类别来判断属于哪个类别。
思想原理
「人以群分,物语类聚」、「近朱者赤,近墨者黑」是 KNN 的核心思想。这其实和我们在日常生活中评价一个人的方法是一样的,如果你想要知道一个人是怎么样的,那就去找和他关系好的几个人看看对他的评价或者看和他关系好的人是什么样子的,就可以大致判断出他是什么样的人了。
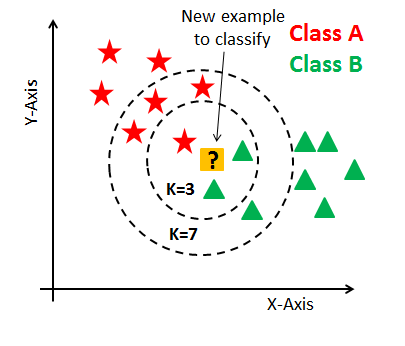
其中的 K 就是 K 个最近的邻居的意思。KNN 的原理就是当预测一个待分类的值 x 的时候,通过计算找出离它距离最近的 K 个样本,然后由这个 K 个样本投票决定 x 归为哪一类。
我们也可以看到实现这个算法的两个核心问题是计算距离和选取 K 的取值。
算法步骤
KNN 算法的步骤:
- 计算未知实例到所有已知实例的距离;
- 选择参数 K(下面会具体讲解K值的相关问题)
- 根据多数表决 ( Majority-Voting ) 规则,将未知实例归类为样本中最多数的类别
更加详细的步骤为:
- 计算测试数据与各个样本数据之间的距离,通常为欧式距离;
- 按照距离的递增关系进行排序;
- 选取距离最小的K个点;
- 确定前K个点所在类别的出现频率;
- 返回前K个点中出现频率最高的类别作为测试数据的预测分类。
动画演示
以下是一个 KNN 算法的动态演示,他能够根据取不同 K 的值将白点归到不同的类别。
当 K 取值不同的时候,判别的结果是不同的。所以该算法中 K 值如何选择将非常重要,因为它会影响到我们最终的结果。
距离计算
KNN 算法中用样本之间的距离来衡量样本之间的相似度。常用的距离有:
- 欧氏距离(Euclidean Distance)
- 曼哈顿距离(Manhattan Distance)
- 明氏距离(Minkowski Distance)
- 切比雪夫距离(Chebyshev Distance)
- 马氏距离
- 汉明距离
- 夹角余弦
- 杰卡德相似系数
其中:
欧式距离最为常用,n 个 p 维样本 x_i 其欧式距离公式如下:
距离的计算本教程会单独做介绍。
特点
算法优点
- 简单,易于理解,易于实现,无需估计参数。
- 对数据没有假设,准确度高,对异常点不敏感。
算法缺点
- 计算量太大,尤其是特征数非常多的时候。每一个待分类文本都要计算它到全体已知样本的距离,才能得到它的第K个最近邻点。
- 样本不平衡的时候,对稀有类别的预测准确率低。当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。
代码示例
K-Nearest Neighbors 是用于分类和回归的机器学习算法(主要用于分类)。它考虑了不同的质心,并使用欧几里得函数来比较距离。接着分析结果并将每个点分类到组中,以优化它,使其与所有最接近的点一起放置。它使用k个最近邻的多数票对数据进行分类预测。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
# Naive Bayes 任务为分类, n_classes=4
import sklearn.naive_bayes as nb
# 1. 准备数据,生成一个随机n类分类问题
nb_X_train, nb_y_train = make_classification(n_features=2, n_redundant=0, n_informative=2,
random_state=1, n_clusters_per_class=1, n_classes=4)
# 2. 构造训练与测试集
l, r = nb_X_train[:, 0].min() - 1, nb_X_train[:, 0].max() + 1
b, t = nb_X_train[:, 1].min() - 1, nb_X_train[:, 1].max() + 1
n = 1000
grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n))
nb_X_test = np.column_stack((grid_x.ravel(), grid_y.ravel()))
# 3. 训练模型
nb_model = nb.GaussianNB()
nb_model.fit(nb_X_train, nb_y_train)
# 4. 预测数据
nb_y_pred = nb_model.predict(nb_X_test)
# 5. 可视化
grid_z = nb_y_pred.reshape(grid_x.shape)
plt.figure('Naive Bayes')
plt.title('Naive Bayes')
plt.pcolormesh(grid_x, grid_y, grid_z, cmap='Blues')
plt.scatter(nb_X_train[:, 0], nb_X_train[:, 1], s=30, c=nb_y_train, cmap='pink')
plt.show()
参考
- https://eunsukimme.github.io/ml/2019/10/20/KNN-classification/