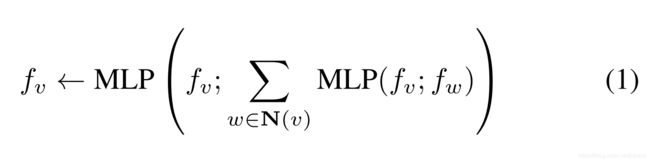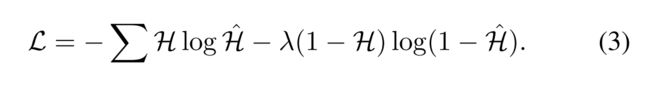【论文翻译】Conv-MPN
《Conv-MPN: Convolutional Message Passing Neural Network for Structured Outdoor Architecture Reconstruction》
链接地址
发表会议: CVPR 2019
Abstract:
本文提出了一种新颖的消息传递神经(MPN)架构Conv-MPN,它可以从单个RGB图像中将室外建筑物重建为平面图。Conv-MPN是专门为图的节点具有显式空间嵌入的情况而设计的。在我们的问题中,节点对应于图像中的建筑物边缘。ConvMPN与MPN的不同之处在于:1)与节点关联的特征表示为特征量而不是一维向量; 2)卷积编码消息而不是完全连接的层。Conv-MPN学习选择节点的真实子集(即建筑物边缘)来重建建筑物平面图。我们对2,000座建筑物的定性和定量评估表明,Conv-MPN在现有的全神经解决方案方面做出了重大改进。我们认为,本文有可能为结构化几何重构开辟一条新的图神经网络研究领域。
1. Introduction
人类的视觉进化成为掌握整体图像的理解,能够检测图像中的结构元素并推断它们之间的关系。看一下图1中的卫星图像。我们可以快速看到三个建筑物组件,检测它们的建筑物拐角,并确定与相邻组件的公共边缘。
这种结构化几何图形的最终形式是CAD表示,它可以实现广泛的应用程序,例如渲染,效果映射,模拟或人机交互。不幸的是,CAD模型的构建对于计算机视觉仍然是一个未解决的问题,只有专家建模者才能实现。
朝着CAD几何的自动构建,深度神经网络(DNN)的出现带来了革命性的改进,用于检测低级图元(例如角)。但是,对高级几何结构的整体理解(例如,图的推断)仍然是DNN的挑战。当前的最新技术使用DNN进行低级基元检测,但采用优化方法进行高级几何结构推断[21,16]。优化功能强大,但是需要复杂的问题表述和深入的工程来注入结构约束。
本文旨在为结构化几何重构的任务拓展深度神经架构的界限。特别是,我们提出了卷积消息传递神经网络(Conv-MPN)。Conv-MPN是图神经网络(GNN)的一种变体,它学习通过交换消息来推断节点的关系。Conv-MPN是专门为节点具有显式空间嵌入的情况而设计的,它与标准消息传递神经网络(MPN)有两个主要区别:1)像CNN一样,节点的特征表示为3D体一维向量和2)卷积编码消息而不是完全连接的层[24、25]或矩阵乘法[5、8]。这种设计允许Conv-MPN利用与节点关联的空间信息。
我们已经证明了Conv-MPN在室外建筑矢量化问题上的有效性[21],其中输入是卫星RGB图像,而输出是描绘内部和外部建筑特征线的平面图。对于计算机视觉来说,这类似于平面向量化是一个具有挑战性的问题,直到最近才有了有效的解决方案[19]。
主要挑战在于推断具有任意拓扑的图结构。由于曼哈顿效应由于缩短效应而无法成立,因此从卫星图像进行室外建筑矢量化的挑战甚至更大。我们还要强调与传统建筑物形状提取问题[1]的区别,后者将建筑物表示为一组像素。
我们对亚特兰大,拉斯维加斯和巴黎等城市的2,000多个复杂建筑实例进行了定性和定量评估[21]。ConvMPN对所有现有的神经解决方案进行了重大改进。我们相信,这项研究有可能为结构化几何重建开辟一条新的图神经网络研究领域。代码和预训练的模型可以在 https://github.com/zhangfuyang/Conv-MPN.
2. Related work
我们首先根据要推断的图结构的层次来回顾结构化的重构技术,然后再对结构化数据使用消息传递技术。
使用固定的拓扑进行重建:使用固定的已知拓扑,由于已经给出了它们的连接,因此图重建就等于简单地检测关键点并对其语义类型进行分类。卷积神经网络已经证明在解决人体姿势估计[22、31、29]和手部追踪[34、38、30]方面有效。
低至中级结构化重构:DNN检测拐角并分类其连接的存在以进行线框解析[15、37、36]。但是,连接分类是针对每个边独立执行的,缺少将图形作为整体考虑的更高层次的几何推理。在遥感中,大多数建筑物提取方法将建筑物表示为一组像素[14]或1D多边形环[2、6、20、7],将输出限制为建筑物外部边界作为1D环。相反,我们试图推断一个对内部和外部体系结构特征线都进行编码的任意拓扑图。
结构化重构(优化):最新的图结构推断结合了CNN和优化,特别是整数编程(IP)[19、18、21]。CNN检测低级几何图元(例如,角)或推断像素方向图信息(例如,边缘似然)。IP融合了所有信息和推断图结构,它虽然功能强大,但需要复杂的问题表述和深入的工程来注入结构约束。
结构化重建(学习):一些方法可以推断出高级几何结构。Ritchie等。 [27]使用DNN通过类似于Lsystem的简单形状语法来学习2D笔画在画布上的排列。Frans等。 [12]。提出了一种无监督的方法来解决这个问题。但是,它们的语法太基本,无法代表建筑结构。Zeng等。 [35]利用建筑形状语法从正射深度图重建室外建筑物。但是,它们的形状语法又过于严格:1)要求进行正射校正以利用曼哈顿假设。 2)仅对小型住宅进行建模。本文不依赖于形状语法,而是从示例中学习结构规律,并在结构推断中加以利用。
消息传递和图形卷积:消息传递已成为高级数据推理的有效工具[23、3、13、17、9、32、4]。一种标准方法是将卷积运算扩展到像素网格上到顶点图[5、17、9、10、23]。布鲁纳等。 [5],Defferand等。
[9]和Kipf等。 [17]利用频谱分析来定义作用在整个图上的图卷积。关键区别在于我们的卷积不会在图域中发生。Conv-MPN拍摄带有显式空间嵌入的图,将节点表示为特征量,并在空间域中执行卷积。该框架允许Conv-MPN利用与图的节点关联的空间信息。
3. Preliminaries
本文从单个卫星图像中解决了2D建筑矢量化问题,其中建筑物以2D平面图表示。本节描述了我们的数据源和预处理步骤(请参见图2)。

图2.初步。给定RGB图像,我们将检测建筑物角候选,枚举凸起边缘候选,然后为节点(建筑物边缘)制定图以进行推断。
数据集:我们的数据源是来自SpaceNet [11]语料库的一组高分辨率卫星RGB图像,作为SpaceNet Challenge [1]的一部分,通过Amazon Web Services(AWS)托管。特别是,我们使用现有的基准[21],将亚特兰大,巴黎和拉斯维加斯等城市的2,001栋建筑物裁剪成256×256正方形图像块[21]。我们使用相同的训练和测试划分(1601/400)以及度量,该度量包括每个角,边和区域图元的精度,查全率和f1分数。请注意,卫星图像是离地面最近的,由于透视效果,建筑物不遵循曼哈顿的假设。
角点候选枚举:给定输入RGB图像补丁I(),我们将Faster-RCNN与ResNet-50用作主干[26],以检测角点候选,同时将每个角视为边界框,并在角上中央。使用SGD对模型进行训练,倾斜率设置为0.0001,批大小为1。
图2.初步。给定RGB图像,我们将检测建筑物角候选,枚举凸起边缘候选,然后为节点(建筑物边缘)制定图以进行推断。
4. Conv-MPN architecture
Conv-MPN背后的基本思想是简单而强大。标准图神经网络(GNN)[4]将几何信息编码为一维矢量,而不是空间上的3D特征。具有1D特征向量的MLP无法进行有效的几何分析,而与3D特征量进行卷积可以实现自然的空间推理。我们的想法是采用标准的MPN体系结构,然后替换1)用潜在的3D体积替换潜在矢量作为特征表示; 2)具有卷积的全连接层(或矩阵乘法),用于消息编码。本节介绍了特定于我们的问题设置的ConvMPN体系结构,但是可以很容易地将框架扩展到整个GNN系列。
4.1. Feature initialization
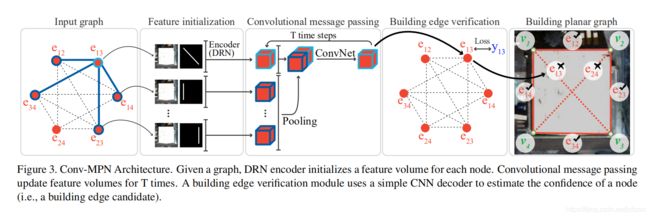
推理图中的节点对应于建筑物边缘,该建筑物边缘将被表示为3D特征量。我们通过将与二进制建筑物边缘蒙版(256×256×4)串联的建筑物RGB图像通过扩散残差网络(DRN)[33]传递来初始化特征量。(见图3)。更具体地说,我们使用DRN-C-26架构的前三个块,然后使用一个3×3第2步卷积进行下采样到64×64×32。在训练过程中,我们通过ImageNet [28]上的预训练权重来初始化网络参数。
4.2. Convolutional message passing
MPN中特征向量更新的标准形式是利用多层感知器(MLP)对消息进行编码并与当前特征混合:
fv表示与节点v相关的特征向量,N(v)表示相邻节点的集合,“;”表示特征串联。
尽管Conv-MPN可以简单地用CNN代替MLP来形成功能更新规则,但是这将需要两个CNN模块,因此需要更多的GPU内存。节点功能遍布整个卷,简单的池化可以将所有信息保留在消息中而不会发生冲突。更准确地说,我们无需为每对节点编码消息,而是将特征跨所有相邻节点合并以编码消息,然后由CNN更新特征向量:
我们对最大池,总池和均值池进行了实验,最大池的效果最佳。由于GPU内存的限制,我们最多执行3次迭代的功能更新。CNN模块由7个Conv-ReLU-BN块组成,这些块不会在不同的迭代中共享。我们使用Conv-MPN(t = x)表示我们的体系结构,其中包含x遍历卷积消息传递。
4.3. Building edge verification
经过几次功能更新迭代后,我们将CNN解码器放置到每个节点并输出置信度分数,以指示相应的建筑物边缘是否为真(见图3)。解码器首先将特征传递到5个ConvReLU-BN块中,以将特征转换为64×64×128。之后,通过最大池化将功能下采样到2×2×128中。最后,将特征平化为512维特征向量,然后是单个完全连接的层以回归置信度分数。
图3. Conv-MPN架构。给定一个图,DRN编码器为每个节点初始化一个特征量。卷积消息传递更新功能量为T次。建筑物边缘验证模块使用简单的CNN解码器来估计节点(即建筑物边缘候选者)的置信度。
4.4. Edge classification loss
H和H帽是地面真实性和建筑物边缘一致性的预测。λ=3用于增加阳性样品的重量。
5. Experiments
我们已经在PyTorch中实施了建议的系统。学习率初始化为,而当测试损失在4个周期内没有减少时,我们将学习率降低0.8。当测试损失在20个星期内没有减少时,我们将终止培训过程。
由于使用3D功能卷,Conv-MPN需要占用大量GPU内存。除Conv-MPN(t = 3)需要两个TitanX GPU外,所有实验均使用一个具有24G内存的NVIDIA TitanX GPU。我们将批次大小设置为1,但会累积梯度并每8批次更新一次参数以抑制噪声梯度。
由于使用3D功能卷,Conv-MPN需要占用大量GPU内存。除Conv-MPN(t = 3)需要两个TitanX GPU外,所有实验均使用一个具有24G内存的NVIDIA TitanX GPU。我们将批次大小设置为1,但会累积梯度并每8批次更新一次参数以抑制噪声梯度。
5.1. Main results
图4显示了通过Conv-MPN进行的代表性平面图重建。该方法能够在不依赖于任何手工约束或先验条件的情况下,恢复超出曼哈顿几何形状的复杂建筑结构。
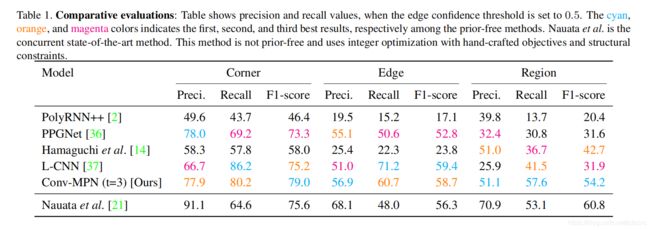
接下来,我们对五种竞争方法进行比较评估:PolyRNN ++ [2],PPGNet [36],Hamaguchi等。 [14],L-CNN [37]和Nauata等。 [21](请参阅表1和图5)。在这里,我们提供了五个方法的简要概述。
- PolyRNN ++以循环方式跟踪建筑物的外部边界[2],并产生一维多边形环。
- PPGNet [36]使用CNN来检测角点并对其连接进行分类。但是,连接(即边)的分类与其他连接无关,缺少高级几何推理。
- PPGNet [36]使用CNN来检测角点并对其连接进行分类。但是,连接(即边)的分类与其他连接无关,缺少高级几何推理。
- L-CNN [37]提出了一种端到端的神经网络,该网络可以检测角并对其连接进行分类。像PPGNet一样,L-CNN也为每个边缘独立执行连接分类。
- L-CNN [37]提出了一种端到端的神经网络,该网络可以检测角并对其连接进行分类。像PPGNet一样,L-CNN也为每个边缘独立执行连接分类。
Nauata等。依靠具有手工目标和结构约束的整数编程。前四种方法和Conv-MPN试图从示例中学习几何规律或先验。
表1显示,Conv-MPN在无先验解决方案中达到了最佳的高阶(区域)指标。对于边角和边缘度量,Conv-MPN并不总是最好的。特别是,在边缘指标上,L-CNN的性能略优于Conv-MPN。但是,如图6所示,由于边缘是独立估计的,因此来自L-CNN的图形结构经常被破坏。图5和图6证明,区域度量最能反映我们平面图结构的感知质量,其中Conv-MPN进行了显着改进。请注意,Conv-MPN落后于Nauata等。 [21]在区域F1分数上,这需要手工制定的目标和结构约束,且需要复杂的IP优化公式。我们想再次强调,Conv-MPN会自动从示例中学习此类先验和约束,这是一项了不起的壮举,并且相对于所有其他先入先出的解决方案进行了重大改进。
5.2. Ablation study
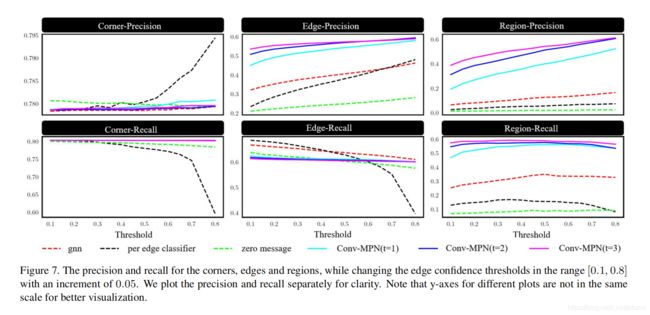
我们验证了Conv-MPN体系结构的贡献,特别是在以下方面的影响:1)特征量表示和2)消息传递。图6和7分别提供了定量和定性的比较。
特征量表示:我们将其与普通GNN进行比较,后者采用Conv-MPN架构,并用512维向量替换(64×64×32)特征量。相应地修改了功能初始化,消息传递和行验证模块,以匹配功能尺寸(有关详细信息,请参阅补充文档)。我们在Conv-MPN和GNN上都进行一次消息传递,以进行清晰的比较。
图7显示,GNN在边缘召回方面提供了竞争性结果,但在其他指标上表现不佳。尤其是对于区域而言,性能差距非常明显,这需要高级几何推理并证明了我们特征表示的力量。
消息传递:我们与两个不进行消息传递的Conv-MPN变体进行了比较。第一个变体(称为“每边缘分类器”)根本没有通过切断节点间连接来交换消息。第二个变体(表示为“零消息”)等效于Conv-MPN(t = 1),但始终会覆盖合并的邻居要素的值为0。

图5.与竞争方法的比较评估。PolyRNN ++ [2],PPGNet [36],Hamaguchi等。 [14]和L-CNN [37]是无先例的现有方法,都利用DNN。 Nauata等。 [21]不是先验的。零消息是我们的Conv-MPN的一种变体,没有传递任何消息。 Conv-MPN是我们的免费系统。
图7显示,Conv-MPN(t = 1)在大多数指标中均优于“边缘分类器”和“零消息”。特别是,区域指标中的性能差距仍然很明显,表明Conv-MPN通过卷积消息传递有效地交换了信息。
图6.特写比较。从左到右分别是L-CNN [37],PPGNet [36],零消息和Conv-MPN(t = 3)。在缩放区域中,我们显示了Conv-MPN可以帮助防止的常见错误。通常,Conv-MPN有助于去除边缘相交,细三角形和连接缺失的边缘。
图7还显示了Conv-MPN如何在卷积消息传递的多次迭代中改善重构(有关定性评估,请参见图4)。从无迭代到1和2迭代,性能改进是一致且强大的,其中每个边缘分类器可以视为Conv-MPN(t = 0)。由于内存限制,Conv-MPN(t = 3)是我们训练的最大模型,它显示出最佳结果,而性能改进开始达到饱和。
5.3. Failure cases
Conv-MPN远非完美,图8显示了故障示例。第一个主要故障模式来自缺失的角落。如果未检测到建筑物拐角,ConvMPN将自动错过所有事件结构。第二种主要故障模式是具有30个或更多候选角的大型建筑物,由于内存限制,它们不会出现在训练集中。
6. Conclusion
本文提出了一种用于结构化室外建筑重建的新型消息传递神经建筑Conv-MPN。我们的想法既简单又强大。 ConvMPN将与节点关联的特征表示为特征量,并利用CNN进行消息传递,同时保留标准的消息传递神经体系结构。定性和定量评估验证了我们的想法的有效性,并证明了与现有的先验解决方案相比,性能得到了显着提高。主要缺点是大量的内存消耗,这是我们将来要解决的工作之一。
图7.边角,边和区域的精度和召回率,同时以0.05的增量更改范围内的边置信度阈值。为了清楚起见,我们分别绘制精度和召回率。请注意,为了获得更好的可视化效果,不同图的y轴的比例不同。
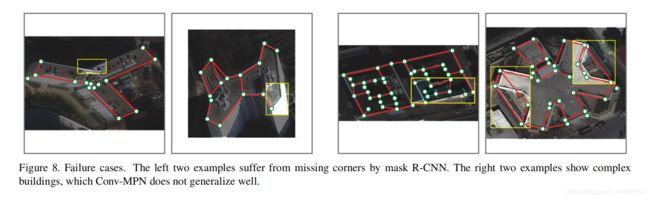
图8.失败案例。左边的两个示例蒙版R-CNN缺少角。右边的两个示例显示了复杂的建筑物,而Conv-MPN不能很好地概括。
当前流行的结构化重建方法是将领域知识作为手工设计的目标或约束注入到优化公式中。ConvMPN从示例中学习了所有这些先验知识,然后推断出平面图结构形成单个图像。我们认为,本文有可能为结构化几何重构开辟一条新的图神经网络研究领域。我们将共享我们的代码和数据以促进进一步的研究。
致谢:NSERC发现补助金,NSERC发现补助金加速器补充和DND / NSERC发现补助金补充部分支持了本研究。情报高级研究项目活动(IARPA)还通过内政部/内政部商务中心(DOI / IBC)合同号D17PC00288支持了此研究。尽管上面有任何版权说明,但美国政府有权为政府目的复制和分发再版。本文包含的观点和结论是作者的观点和结论,不应解释为必然代表IARPA,DOI / IBC或美国政府的官方政策或认可,无论是明示或暗示。