【论文笔记 - 图像生成 - CVPR2022】Exploring Dual-task Correlation for Pose Guided Person Image Generation

论文地址：https://arxiv.org/pdf/2203.02910.pdf
代码地址：https://github.com/PangzeCheung/Dual-task-Pose-Transformer-Network

姿势引导人物图像生成是将人物图像从源姿势转换为给定目标姿势的任务，作者认为现有的方法大多只针对不适定的源到目标任务，无法捕捉到合理的纹理映射。为了解决这个问题，提出了一种新的双任务姿势变换网络（Dual-task Pose Transformer Network，$DPTN$），引入了源到源的辅助任务，并通过姿势变换模块（Pose Transformer Module，$PTM$） 充分利用双任务的相关性来提高姿态迁移的性能，

• $Source\text{-}to\text{-}SourceTask$，源图像到源图像自重构分支，即生成原图，

• $Source\text{-}to\text{-}TargetTask$，源图像到目标图像的转换分支，即生成有原图像纹理和目标姿态的图像

1. 模型结构

如下图所示，$DPTN$ 为连体结构，包含 $Self\text{-}reconstructionBranch$ 和 $TransformationBranch$ 两部分，它们之间共享部分权重，这样源到源任务所学习的知识可以有效地帮助源到目标的学习。此外，作者还使用姿势变换模块 $PTM$ 将两个分支任务连接起来，自适应地探索来自两个任务的特征之间的相关性，在源和目标之间建立所有像素的细粒度映射，同时，促进源纹理传输以增强生成的目标图像的细节。

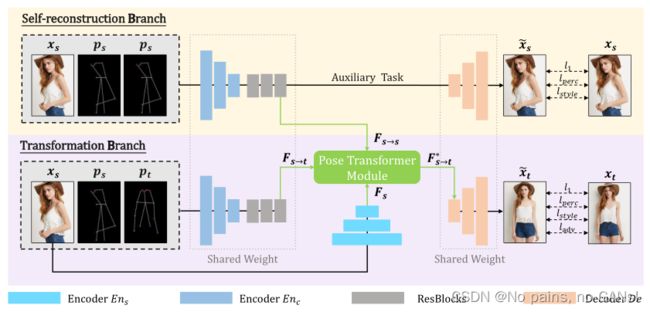
1.1 Siamese Structure for Dual Tasks

作者认为，从源到目标任务的学习不能很好利用源图像的细节，并通过实验验证了，在不修改传统姿态迁移网络的前提下，单纯加入源到源的训练，也就是 $self\text{-}reconstuctiontraining$，就可以提升模型效果，

基于此，作者将源到源任务添加到模型中，利用学到的知识，来帮助训练过程中源到目标的转换。

网络结构如上图所示，具体来说，分为以下几个步骤，

• 编码器 $Encoder$ 提取两种输入的特征，
• 应用 $ResBlocks$ 逐步进行姿态变换，得到与源姿态对齐的 ${\mathbf{F}}_{s\to s}$ 和与目标姿态对齐的 ${\mathbf{F}}_{s\to t}$，
• $Self\text{-}reconstructionBranch$，解码器 $Decoder$ 根据 ${\mathbf{F}}_{s\to s}$ 生成假源图，
• $TransformationBranch$，编码器 $Decoder$ 根据改善的 ${\mathbf{F}}_{s\to t}^{\ast }$ 生成目标图片，

作者认为这样设计有如下优点，

• 共享权重，因此学习的知识可以在两个任务之间轻松地转移，并且引入的$Self\text{-}reconstructionBranch$ 不会大幅增加额外的参数
• 连体结构使双任务的中间输出在特征分布上接近，便于 $PTM$ 探索双任务的相关性。

1.2 Pose Transformer Module

由于基于 $CNN$ 的变换分支（即源到目标）难以处理复杂的空间变形，${\mathbf{F}}_{s\to t}$ 往往会丢失许多源外观细节，如下图所示，

因此，作者提出了基于多头注意力机制的 $PTM$，通过捕获双任务特征之间的对应关系，改善 ${\mathbf{F}}_{s\to t}$。具体结构如下所示，

包含两大模块，

• 包含上下文增强模块（Context Augment Block，$CAB$），整合来自 ${\mathbf{F}}_{s\to s}$ 的信息，

• 纹理迁移模块（Texture Transfer Block，$TTB$），根据 ${\mathbf{F}}_s$ 中的真实源图像纹理来优化 ${\mathbf{F}}_{s\to t}$ ，使其捕获双重任务中特征之间的相关性。

1.2.1 Context Augment Block

上图右侧展示了 $CAB$ 的具体结构，首先应用带有残差连接的多头自注意力 （Multi-Head Self-Attention，$MHSA$），自适应地增强输入特征的上下文表示，

${\tilde{\mathbf{F}}}_{s\to s}^i=IN\left({\mathbf{F}}_{s\to s}^{i-1}+\mathrm{MHSA}\left({\mathbf{F}}_{s\to s}^{i-1},{\mathbf{F}}_{s\to s}^{i-1},{\mathbf{F}}_{s\to s}^{i-1}\right)\right)$

然后使用具有多个全连接层的 $MLP$ 模块来增加网络容量，

${\mathbf{F}}_{s\to s}^i=IN\left({\tilde{\mathbf{F}}}_{\mathbf{s}\to \mathbf{s}}^i+MLP\left({\tilde{\mathbf{F}}}_{\mathbf{s}\to \mathbf{s}}^i\right)\right)$

经过 $N$ 个 $CAB$ 模块后，得到了最终改善的特征 ${\mathbf{F}}_{s\to s}^N$ ，并将其应用于源到目标任务的每个 $TTB$ 中。

1.2.2 Texture Transfer Block

首先应用带有残差连接的 $MHSA$ ，使模型注意 ${\mathbf{F}}_{s\to t}^{i-1}$ 的关键信息，

${\tilde{\mathbf{F}}}_{s\to t}^i=IN\left({\mathbf{F}}_{s\to t}^{i-1}+MHSA\left({\mathbf{F}}_{s\to t}^{i-1},{\mathbf{F}}_{s\to t}^{i-1},{\mathbf{F}}_{s\to t}^{i-1}\right)\right)$

然后通过多头交叉注意力 （Multi-Head Cross-Attention，$MHCA$）来建立 ${\tilde{\mathbf{F}}}_{s\to t}^i,{\mathbf{F}}_{s\to s}^N,{\mathbf{F}}_s$ 的关系。具体来说，${\tilde{\mathbf{F}}}_{s\to t}^i,{\mathbf{F}}_{s\to s}^N$ 分别为 $queries$ 和 $keys$，用于计算源和目标像素之间的相似性，借助于此，${\mathbf{F}}_s$ 在 $MHCA$ 中被用作 $values$，用真实图像的纹理特征以改善 ${\tilde{\mathbf{F}}}_{s\to t}^i$，

${\hat{\mathbf{F}}}_{s\to t}^i=IN\left({\tilde{\mathbf{F}}}_{s\to t}^i+MHCA\left({\tilde{\mathbf{F}}}_{s\to t}^i,{\mathbf{F}}_{s\to s}^N,{\mathbf{F}}_s\right)\right)$

这样，${\tilde{\mathbf{F}}}_{s\to t}^i$ 就具有更真实的源纹理，这将促进 $TransformationBranch$ 生成更精细的图像。最后，与 $CAB$ 类似采用了 $MLP$。

${\mathbf{F}}_{s\to t}^i=IN\left({\hat{\mathbf{F}}}_{s\to t}^i+MLP\left({\hat{\mathbf{F}}}_{s\to t}^i\right)\right)$

经过 $N$ 个 $TTB$ 模块后，得到了最终的输出特征 ${\mathbf{F}}_{s\to t}^N$ ，并将其应用于 $Decoder$ 中生成目标图像 ${\tilde{x}}_t$。

2. 损失函数

$dualtasks$ 总的损失为，

$\mathcal{L}={\mathcal{L}}_{s\to s}+{\mathcal{L}}_{s\to t}$

${\mathcal{L}}_{s\to s},{\mathcal{L}}_{s\to t}$ 分别表示源到源、源到目标的损失，它们都包含了 $l_1$ 损失 ${\mathcal{L}}_{l_1}$，感知损失 ${\mathcal{L}}_{perc}$ 和风格损失 ${\mathcal{L}}_{style}$，显然，在源到目标任务中还需要一个对抗损失 ${\mathcal{L}}_{adv}$ 来产生更逼真的纹理。

就可以得到如下的式子，

${\mathcal{L}}_{s\to s}={\lambda }_{l_1}{\mathcal{L}}_{l_1}^s+{\lambda }_{\text{perc }}{\mathcal{L}}_{\text{perc }}^s+{\lambda }_{\text{style }}{\mathcal{L}}_{\text{style }}^s$

${\mathcal{L}}_{s\to t}={\lambda }_{l_1}{\mathcal{L}}_{l_1}^t+{\lambda }_{\text{perc }}{\mathcal{L}}_{\text{perc }}^t+{\lambda }_{\text{style }}{\mathcal{L}}_{\text{style }}^t+{\lambda }_{adv}{\mathcal{L}}_{adv}$

在具体一点，

$l_1$ 损失惩罚生成的图像和真实图像之间的 $l_1$ 距离，

${\mathcal{L}}_{l_1}^d={\Vert {\mathbf{x}}_{\mathbf{d}}-{\tilde{\mathbf{x}}}_{\mathbf{d}}\Vert }_1$

感知损失计算图像之间的特征距离，${\varphi }_i$ 表示 $VGG$ 的第 $i$ 个特征，

${\mathcal{L}}_{\text{perc }}^d={\sum }_i{\Vert {\varphi }_i\left({\mathbf{x}}_{\mathbf{d}}\right)-{\varphi }_i\left({\tilde{\mathbf{x}}}_{\mathbf{d}}\right)\Vert }_1$

风格损失比较了图像之间的风格相似性，${\mathrm{Gram}}_j^{\varphi }$ 是 ${\varphi }_j$ 的特征矩阵，

${\mathcal{L}}_{\text{style }}^d={\sum }_j{\Vert {\mathrm{Gram}}_j^{\varphi }\left({\mathbf{x}}_{\mathbf{d}}\right)-{\mathrm{Gram}}_j^{\varphi }\left({\tilde{\mathbf{x}}}_{\mathbf{d}}\right)\Vert }_1$

对抗损失用于惩罚生成图像 ${\tilde{x}}_t$ 和真实图像 $x_t$ 分布的差异，

${\mathcal{L}}_{adv}=\mathbb{E}\left[\log \left(1-D\left({\tilde{\mathbf{x}}}_{\mathbf{t}}\right)\right)\right]+\mathbb{E}\left[\log D\left({\mathbf{x}}_{\mathbf{t}}\right)\right]$