大厂面试机器学习算法（1）SVM常考问题

网易有道数据挖掘面试题：介绍svm的原理
字节跳动机器学习算法面试题：手推svm过程

今天整理一下面试常考问题。

1. SVM算法原理

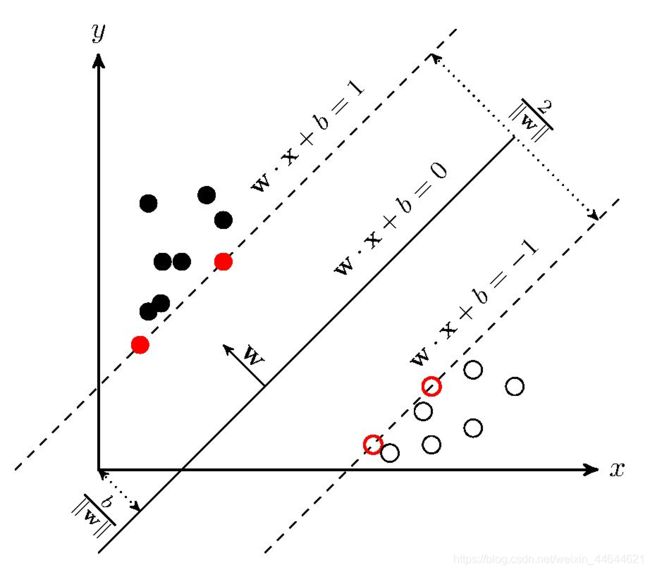
SVM的基本原理是求解能够正确划分训练数据集并且几何间隔最大的超平面。
如图1， $wx+b=1$和 $wx+b=-1$ 即为所求超平面。

2. SVM与感知机(Perceptron)/逻辑回归（LR）的区别

1. 与感知机：
   感知机所求超平面为$wx+b=0$，对于线性可分数据集有无穷多个。而SVM所求间隔最大的超平面结果唯一。
2. 与LR：
   svm只考虑支持向量点，LR考虑所有样本；
   svm是非参数模型，LR是参数模型；
   svm的目标函数是hinge损失函数，LR采用logistics损失函数
   svm自带结构风险最小化（$1/||w|{|}^2$)，LR是经验风险最小化
   svm产生区间，LR产生概率

3. 什么是支持向量

对线性可分的情形，构造硬间隔，位于间隔边界上的样本点称为支持向量；
对线性不可分的情形，构造软间隔，位于间隔边界上及间隔边界之内的样本点的实例称为支持向量。

4. 手推SVM最优化公式

目标：最大化异类支持向量的间隔。
① 点$(x_i,y_i)$到直线$wx+b=0$的距离$d=y_i(\frac{w{x}_i+b}{||w||})$
② 支持向量：位于间隔边界线上的点，即$\underset{(x_i,y_i)}{\min }{y}_i(\frac{w{x}_i+b}{||w||})$
③ 最大化异类支持向量间隔，即 $\underset{w,b}{\max }\underset{(x_i,y_i)}{\min }{y}_i(\frac{w{x}_i+b}{||w||})$
④ 根据几何直线的可缩放性质（x+y=0<=>2x+2y=0），对$\forall w,b$，可通过缩放使得$\underset{(x_i,y_i)}{\min }{y}_i(w{x}_i+b)$=1，即 $y_i(w{x}_i+b)\ge 1$
因此目标函数等价于$\underset{w,b}{\max }\frac{1}{||w||}$
又等价于：
$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2$
s.t. $y_i(w{x}_i+b)\ge 1$
即支持向量机的最优化公式。

5. SVM使用对偶计算的目的是什么？如何推导出来的？

目的有两个：

1. 方便核函数的引入；
2. 原问题的求解复杂度与特征的维数相关，而转成对偶问题后只与变量个数有关。而SVM的变量个数为支持向量的个数，相较于特征位数较少。

通过拉格朗日算子法使带约束的优化目标转为不带约束的优化函数，
即由：$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2$
s.t. $y_i(w{x}_i+b)\ge 1$
写出拉格朗日函数$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+{\sum }_{i=1}^m{\alpha }_i(1-y_i(w{x}_i+b))$,
令w和b的偏导数等于零，得：
$w={\sum }_{i=1}^m{\alpha }_i{y}_i{x}_i$
$0={\sum }_{i=1}^m{\alpha }_i{y}_i$
带入原来的式子，即转成对偶问题：$\underset{\alpha }{\max }{\sum }_{i=1}^m{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi (x_i{)}^T\varphi (x_j)$
s.t. ${\sum }_{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,...m.$

6. SVM中什么时候用线性核什么时候用高斯核?

对[n,m]数据集（即n个样本，m个特征）：
线性核函数：
① 当数据的特征提取的较好,所包含的信息量足够大,很多问题是线性可分的，一般用线性核函数，直接实现可分；
② 若样本n和特征m很大时，且特征m>>n时，需要用线性核函数，因为此时考虑高斯核函数的映射后空间维数更高，更复杂，也容易过拟合，此时使用高斯核函数的弊大于利，选择使用线性核会更好；
③ 若样本n很大，但特征m较小，同样难以避免计算复杂的问题，因此会更多考虑线性核。
高斯核函数：
① 当训练数据不可分时，需要使用核技巧，将训练数据映射到另一个高维空间，使再高维空间中，数据可线性划分；
② 若样本n一般大小，特征m较小，此时进行高斯核函数映射后，不仅能够实现将原训练数据在高维空间中实现线性划分，而且计算方面不会有很大的消耗，因此利大于弊，适合用高斯核函数。

核函数是什么？

$\varphi (x)$为x的高维映射；
$K(x,y)=<\varphi (x),\varphi (y)>$为核函数（"< , >"符号表示内积）；
例：设$x=(1,2,3,4),y=(5,6,7,8)$，
将$x=(x_1,x_2,x_3,x_4)$映射为$\varphi (x)=\left[\begin{array}{cccc}{x}_1^2& x_1{x}_2& x_1{x}_3& x_1{x}_4\\ x_2{x}_1& x_2^2& x_2{x}_3& x_2{x}_4\\ x_3{x}_1& x_3{x}_2& x_3^2& x_3{x}_4\\ x_4{x}_1& x_4{x}_2& x_4{x}_3& x_4^2\end{array}\right]$；
$K(x,y)=<\varphi (x),\varphi (y)>=<x,y{>}^2$
则$\begin{array}{rl}<\varphi (x),\varphi (y)>& =<(1,2,3,4,2,4,6,8,3,6,9,12,4,8,12,16),(25,30,35,40,30,36,42,48,35,42,49,56,40,48,56,64)>\\ & =25+60+105+160+60+144+252+384+105+252+441+672+160+384+672+1024\\ & =4900\end{array}$
而$K(x,y)=(5+12+21+32{)}^2$=4900
由此可见，核函数是对两个高维映射函数的内积运算的简便运算。

为什么SVM需要核函数？

将4. 最优化公式转化为5. 对偶形式后需要进行求解，对偶问题推导为：
$\underset{\alpha }{\max }{\sum }_{i=1}^m{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi (x_i{)}^T\varphi (x_j)$ （$x_i$和$x_j$为任意两个样本点）
s.t. ${\sum }_{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,...m.$
此处我们便可以通过核函数来计算上式中的$\varphi (x_i{)}^T\varphi (x_j)$。

实际上，将低维样本点（在上例中为4维）映射为高维样本（16维）的函数是$\varphi (x)$，
而K(x,y)是为简化计算$\varphi (x_i{)}^T\varphi (x_j)$引入的核函数。
在很多计算中，我们不需要计算复杂的$\varphi (x)$，只需要计算简单的K(x,y)即可得到结果。

7. SVM的硬间隔、软间隔表达式

硬间隔： $\underset{w,b}{\min }\frac{1}{2}||w|{|}^2$
s.t. $y_i(w{x}_i+b)\ge 1$

软间隔： $\underset{w,b}{\min }\frac{1}{2}||w|{|}^2+C{\sum }_{i=1}^m{\xi }_i$
s.t. $y_i(w{x}_i+b)\ge 1-{\xi }_i,$
${\xi }_i\ge 0,i=1,2,...,m.$
不同点在于有无引入松弛变量。
其中，hinge损失的松弛变量为$max(0,y_i(w{x}_i+b))$
损失函数变为$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2+C{\sum }_{i=1}^{m}max(0,y_i(w{x}_i+b))$