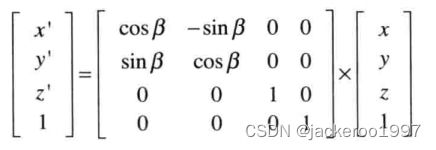webgl变换矩阵理论详解
文章目录
- 前言
- 矩阵运算
-
- 矩阵加减
- 矩阵数乘
- 矩阵乘矩阵
- 矩阵转置
- 逆矩阵
- 正交矩阵
- 矩阵变换的一般规则
-
- 行主序和列主序
- 行向量和列向量
- 复杂变换时的顺序
- 变换矩阵进行图形变换
-
- uniform传递矩阵
- 平移
- 缩放
- 旋转
- 组合变换实例
- 总结
前言
在webgl中将图形进行平移、旋转、缩放等操作时可以在着色器中使用数学表达式来操作,但是这样并不是最好的方式,当进行的变换比较复杂,如“旋转后平移再缩放”这样的场景,每次都要先重新计算表达式,然后在着色器中去更改它,这样很不方便,因此,出现了另一种数学手段——变换矩阵,变换矩阵非常适合处理计算机图形。本文对变换矩阵的理论进行讲解。
矩阵运算
矩阵是按照行列排列的一系列数值得的集合,由 m × n 个数排成的m行n列的数表称为m行n列的矩阵,简称m × n 矩阵,如下图。当 m 和 n 相同则称这个方阵为 m 阶矩阵(方阵)。
矩阵加减
应该注意的是只有同型矩阵之间才可以进行加减,即为行数和列数都必须一样的两个矩阵才可以进行加减运算。矩阵加减运算的规则是将将两个矩阵对应位置上的元素相加减:
矩阵数乘
矩阵和标量相乘,返回一个新矩阵,新矩阵的各个元素等于原矩阵各个元素与标量的乘积:

矩阵乘矩阵
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积C是一个m×p矩阵,规则如下:
矩阵相乘满足分配律和结合律,但不满足交换律:
矩阵转置
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵 A T A^{T} AT

逆矩阵
设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得: AB=BA=E ,则称方阵A可逆,并称方阵B是A的逆矩阵,单位矩阵是一个对角线上的元素都为1的方阵,其余元素为 0,比如下面就是一个 3 阶单位矩阵:
不是所有的矩阵都存在逆矩阵,逆矩阵首先必须是方阵,而且存在与其相乘结果为单位矩阵的矩阵在图形学中,将进行矩阵变换的坐标再乘以该变换矩阵的逆矩阵,可以将变换后的坐标再还原回去,实现撤销的效果
正交矩阵
假设有一个方阵M,当且仅当 M 与其转置矩阵M^T的乘积等于单位矩阵时,称其为正交矩阵。即:
![]()
即:
![]()
此时方阵M为一个正交矩阵,矩阵正交需要满足以下两个条件:
- 矩阵的每一行都是单位向量
- 矩阵的某一行和其他行向量相互垂直,点积为 0
两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为:a·b=a1*b1 + a2*b2 + … + an*bn
矩阵变换的一般规则
行主序和列主序
在JavaScript中,没有专门用来表示矩阵的类型,需要使用类型化数组new Float32Array来存储,但是数组是一维的,矩阵是二维的,将二维的矩阵存储到一维数组中有两个方式:行主序和列主序。
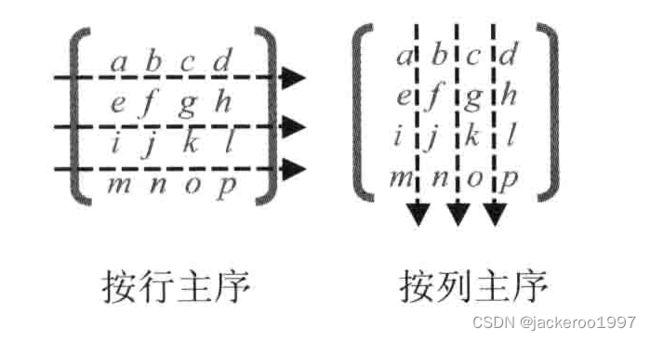
webgl按照列主序的规则将矩阵存储于数组,对于上面这个矩阵,按照列主序存到数组中一个是这样的:
new Float32Array([ a, e, i, m, b, f, j, n, c, g, k, o, d, h, l, p,])
一般在程序中这样书写,看起来更加舒服
new Float32Array([
a, e, i, m,
b, f, j, n,
c, g, k, o,
d, h, l, p,
])
行向量和列向量
- 如果是行向量,向量要放在左侧相乘。
- 如果是列向量,向量要放在右侧相乘。
着色器中vec[i]类型的数据都是在乘号的右侧,由此推断他们都是列向量
复杂变换时的顺序
在多个矩阵变换时,不同的相乘顺序会导致不同的结果,按照理解成本最低的准则,通常是第一步缩放,之后旋转,最后平移
P’ = <平移矩阵> * <旋转矩阵> * <缩放矩阵> * P
变换矩阵进行图形变换
uniform传递矩阵
uniform的使用与前面文章使用的区别不大,创建uniform变量并绑定至着色器 => 向顶点着色器传输变量 => 顶点着色器接收并使用unifrom变量。这里有一个新出现的方法 gl.uniformMatrix4fv()。
gl.uniformMatrix4fv(loaction, transpose, array) 将 4*4的矩阵array分配给由location指定的uniform变量
- location:uniform变量存储位置
- transpose:false
- array: Float32Array类型化数组,必须是列主序
transpose表示是否开启转置矩阵,webgl中没有提供该方法,因此必须设置为false
平移
平移的数学原理很容易理解,在x y z的基础上分别加上一个平移量即可:
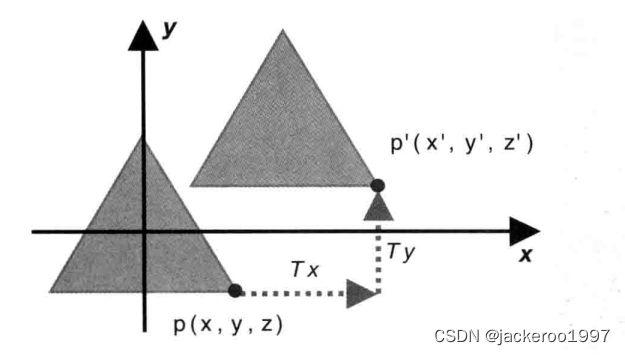
- x’ = x + Tx
- y’ = y + Ty
- z’ = z + Tz
但是这里有一个问题:根据前面矩阵相乘的理论,n维矩阵和n维向量相乘,不能实现向量和一个常量进行加减的操作:
为了解决这个问题,结合之前齐次坐标系的知识,可以使用一个4维的矩阵,同时将点坐标也扩充为vec4,设原始点坐标为(x,y,z,1),平移后点坐标为(x’,y’,z’,1):
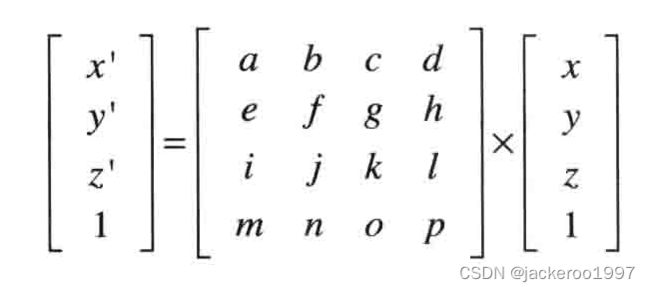
换为表达式的形式则为:
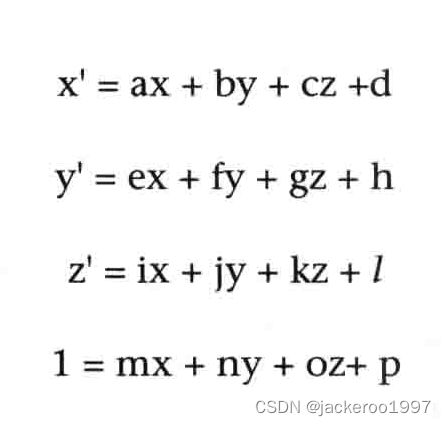
比较x’,可得a=1,b=0,c=0,d=Tx;比较y’,可得f=1,e=0,g=0,h=Ty;比较z’,可得k=1,i=0,j=0,l=Tz;由此可得平移矩阵的表达式:
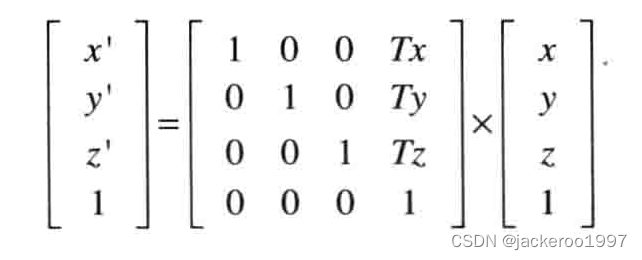
完整示例如下,initShader在之前声明过。基于变换矩阵实现平移动画效果。
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>webgl</title>
<script src="./lib.js"></script>
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<style>
body {
margin: 0;
padding: 0;
}
canvas {
margin: 50px 30px;
width: 500px;
height: 500px;
background-color: antiquewhite;
}
</style>
</head>
<body>
<canvas id="canvas"></canvas>
<script>
/** @type {HTMLCanvasElement} */
//------------------------------------------------------创建画布
// 获取canvas元素对象
let canvas = document.getElementById('canvas');
// 获取webgl绘图上下文
const gl = canvas.getContext('webgl');
if (!gl) {
throw new Error('WebGL not supported');
}
canvas.width = 500;
canvas.height = 500;
gl.viewport(0, 0, canvas.width, canvas.height)
const vertex = `
attribute vec4 aPosition;
uniform mat4 mat;
void main() {
gl_Position = mat * aPosition;
}
`
const fragment = `
precision highp float;
void main(){
gl_FragColor =vec4(1.0,1.0,0.0,1.0);
}
`
// 创建program
const program = initShader(gl, vertex, fragment)
// 获取attribute变量的数据存储位置
const aPosition = gl.getAttribLocation(program, 'aPosition');
const mat = gl.getUniformLocation(program, 'mat');
// 创建缓冲区对象
const buffer = gl.createBuffer();
// 绑定缓冲区对象
gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
// 传入的数据
const vertices = new Float32Array([
-0.5, -0.5, // 顶点着色器补全为(0.0,0.5,0.0,1.0)
0.5, -0.5,
0.0, 0.5
])
// 开辟空间并写入数据
gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW)
// 缓冲区对象分配给attribute变量
gl.vertexAttribPointer(aPosition, 2, gl.FLOAT, false, 0, 0)
// 开启attribue缓冲区变量
gl.enableVertexAttribArray(aPosition)
function getTranslateMatrix(x=0, y=0, z=0){
return new Float32Array([
1.0, 0.0, 0.0, 0.0,
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
x, y, z, 1,
])
}
let translate = 0
function animate() {
console.log('requestAnimationFrame')
translate += 0.01;
if (translate > 1.5) {
translate = 0
}
const matT = getTranslateMatrix(translate)
gl.uniformMatrix4fv(mat, false, matT)
// 开始绘制
gl.drawArrays(gl.TRIANGLES, 0, 3)
const timer = requestAnimationFrame(() => animate())
}
// 销毁定时器
function removeAnimate(){
cancelAnimationFrame(timer)
}
animate()
</script>
</body>
</html>
缩放
- x’ = Sx * x
- y’ = Sy * y
- z’ = Sz * z
变换矩阵如下,像这种进行转置之后仍然不变的矩阵,称为对称矩阵,缩放矩阵就是一个对阵矩阵。

旋转
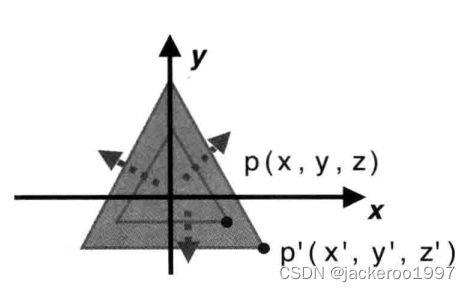
在前一篇文章中对旋转矩阵有过推导,这里直接晒出结论
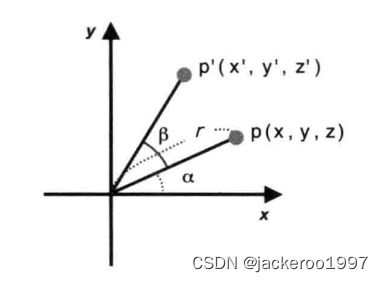
假设原本齐次坐标系上一点P的坐标是(x,y,z),经逆时针旋转角度β后移动至P’(x’, y’, z’),r表示原点到旋转前的P的距离,α是X轴旋转到P的角度。则P的坐标可以表示为:
- x’ = x * cos β - y * sin β
- y’ = x * sin β + y * cos β
- z’ =z
组合变换实例
结合上述理论,我们可以在着色器中传入平移、旋转和缩放矩阵,计算新的坐标,实现动画效果。但是在javascript中提前计算好最终的变换矩阵,然后只穿一个uniform变量是更好的方式,threejs提供了这样的矩阵工具,但是webgl没有提供矩阵计算的工具函数,有兴趣的话可以自己编写。
示例和代码如下:

<body>
<canvas id="canvas"></canvas>
<script>
/** @type {HTMLCanvasElement} */
//------------------------------------------------------创建画布
// 获取canvas元素对象
let canvas = document.getElementById('canvas');
// 获取webgl绘图上下文
const gl = canvas.getContext('webgl');
if (!gl) {
throw new Error('WebGL not supported');
}
canvas.width = 500;
canvas.height = 500;
gl.viewport(0, 0, canvas.width, canvas.height)
const vertex = `
attribute vec4 aPosition;
uniform mat4 matTranslate;
uniform mat4 matScale;
uniform mat4 matRotate;
void main() {
gl_Position = matTranslate * matRotate * matScale * aPosition;
}
`
const fragment = `
precision highp float;
void main(){
gl_FragColor =vec4(1.0,1.0,0.0,1.0);
}
`
// 创建program
const program = initShader(gl, vertex, fragment)
// 获取attribute变量的数据存储位置
const aPosition = gl.getAttribLocation(program, 'aPosition');
const matTranslate = gl.getUniformLocation(program, 'matTranslate');
const matScale = gl.getUniformLocation(program, 'matScale');
const matRotate = gl.getUniformLocation(program, 'matRotate');
// 创建缓冲区对象
const buffer = gl.createBuffer();
// 绑定缓冲区对象
gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
// 传入的数据
const vertices = new Float32Array([
-0.2, -0.2, // 顶点着色器补全为(0.0,0.5,0.0,1.0)
0.2, -0.2,
0.0, 0.2
])
// 开辟空间并写入数据
gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW)
// 缓冲区对象分配给attribute变量
gl.vertexAttribPointer(aPosition, 2, gl.FLOAT, false, 0, 0)
// 开启attribue缓冲区变量
gl.enableVertexAttribArray(aPosition)
function getTranslateMatrix(x=0, y=0, z=0){
return new Float32Array([
1.0, 0.0, 0.0, 0.0,
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
x, y, z, 1,
])
}
function getScaleMatrix(S = 1){
return new Float32Array([
S, 0.0, 0.0, 0.0,
0.0, S, 0.0, 0.0,
0.0, 0.0, S, 0.0,
0.0, 0.0, 0.0, 1
])
}
function getRotateMatrix(deg){
return new Float32Array([
Math.cos(deg), Math.sin(deg), 0.0, 0.0,
-Math.sin(deg), Math.cos(deg), 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0,
])
}
let translate = 0
let scale = 1
let deg = 0
function animate() {
console.log('requestAnimationFrame')
translate += 0.01;
scale += 0.003;
deg += 0.01;
if (translate > 1.5) {
translate = 0
}
if (scale > 2) {
scale = 1
}
const matT = getTranslateMatrix(translate)
const matS = getScaleMatrix(scale)
const matR = getRotateMatrix(deg)
gl.uniformMatrix4fv(matTranslate, false, matT)
gl.uniformMatrix4fv(matScale, false, matS)
gl.uniformMatrix4fv(matRotate, false, matR)
// 开始绘制
gl.drawArrays(gl.TRIANGLES, 0, 3)
const timer = requestAnimationFrame(() => animate())
}
// 销毁定时器
function removeAnimate(){
cancelAnimationFrame(timer)
}
animate()
</script>
</body>
总结
- 矩阵运算
加减、矩阵数乘、矩阵乘矩阵、矩阵转置、逆矩阵、正交矩阵 - 矩阵变换的一般规则
行主序和列主序、行向量和列向量、复杂变换时的顺序 - 变换矩阵进行图形变换
uniform传递矩阵、平移、缩放、旋转 - 组合变换实例