Python实现函数可视化--快捷显示数学函数图像的轻量级工具制作教程
Python函数可视化工具
目录
1.简介
对于如今的中学生乃至大学生,只要接触到数学相关内容的,就必然离不开函数这一“生死大关”。为什么说是生死大关呢?实在是函数类问题太令人头疼。那么,在进行此类解题(尤其是三角函数)及性质研究时,有没有一种方便、快捷的方法,让我们能够更透彻地,特别是不用手动画图的那种,研究函数的性质呢?当然有,这就是Python函数图像工具(EXE) 。
本程序运用Python中最令人喜爱的数据处理工具numpy和超强的图像库matplotlib,实现13种不同类别函数的分类图像整理,展示图像均可以保存为图片的形式,具备拖动、放大等功能。当然,因为教程的关系,我们就不再多说,有兴趣的小伙伴可以点击上方链接运行试一下。详细介绍:Python函数图像工具介绍
2.教程 -- 一次函数
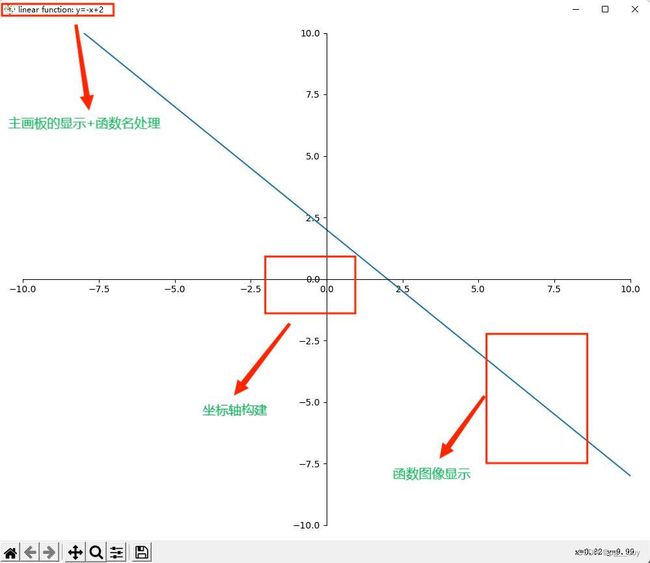
先上效果图(当然只是1/13的成果):
从这里不难看出,整个一次函数图像的显示总共分为3步:分别是【主画板显示+函数名处理】、【坐标轴构建】以及【函数图像显示】。我们一块一块来说。
1)倒库
import matplotlib.pyplot as plt #图像库
import numpy as np #数据处理
import math #数学计算2)主画板显示+函数名处理
主画板主要就是 plt.plot() 的构建,但注意我们还要命名,构建坐标轴等,所以先用 figure()来代替一下,结尾是 plt.tight_layout()。
x = np.linspace(left, right, abs(100*left*right)) #规定区间,第三个空是精度,太高会耗内存
#y = ax+b --函数操作,当然现在是数学语言
fig = plt.figure(title, figsize=(10, 8)) #title是名字,figsize窗口大小
fig.canvas.manager.window.wm_geometry('+450+50') #固定窗口位置
plt.tight_layout()那么现在就要考虑函数名的问题了,这其实也是非常难搞的事情,如果操作不当,就会出很大的问题。
函数y=ax+b中,我们一定要确定的几种特殊情况是:
1.a=0时,y=b;a=1时,y=x+b;a=-1时,y=-x+b(不能写b-x)
2.b=0时,y=ax;b<0时,y=ax-|b|(不能输出加号)
那么,我们就可以尝试构建代码了(这里coefficient1表示一次项系数,也就是a,constant是系数,str_cfc和str_cst分别表示处理过的字符串格式的数据):
x = np.linspace(left, right, abs(100*left*right))
#y = ax+b
#数据处理
if coefficient_1 > 0:
if coefficient_1 == 1:
str_cfc1 = "x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
elif constant > 0:
str_cst = "+"+str(constant)
else:
str_cst = str(constant)
else:
if coefficient_1 == -1:
str_cfc1 = "-x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
elif constant > 0:
str_cst = "+"+str(constant)
else:
str_cst = "+"+str(constant)
#linear funscion 一次函数的名称搭建
fig = plt.figure("linear function: y="+str_cfc1 + str_cst, figsize=(10, 8))
fig.canvas.manager.window.wm_geometry('+450+50')
plt.tight_layout()
plt.show() #显示图像给数据随便赋个值(注意left应该<=0,否则后面会有问题),运行结果:
可以明显看出,程序已经初具雏形了。
3)坐标轴构建+函数图像显示
事实上,坐标轴的构建就是把x,y轴从左下角拉到中间,再表上数值的过程。上代码:
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
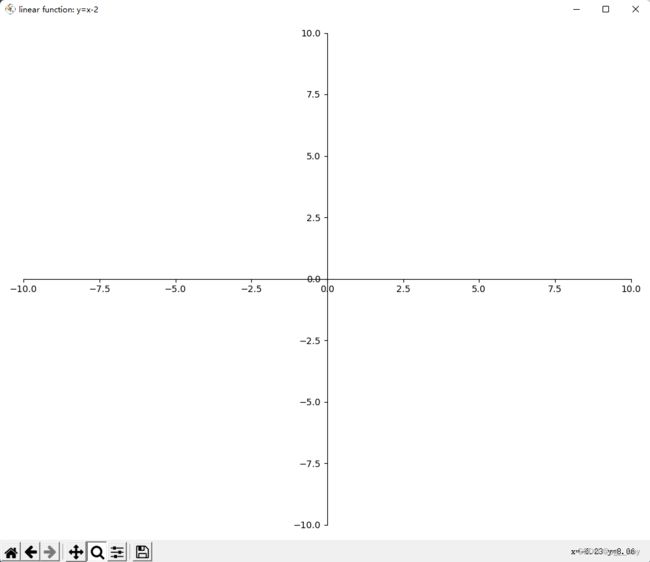
ax.spines['left'].set_position(('data', 0))加上这一段话,运行结果:
真的已经和最终结果相差不远了,那么差点什么呢......没错!函数图像!!!
别忘了我们的目标是做出Python函数图像工具,现在万事俱备,最为关键的函数可不能少。
继续分析:
在前面的代码中,我们已经知道了x的值:
x = np.linspace(left, right, abs(100*left*right))没错,x坐标的集合就是在 (left, right) 的区间内的每一个取值,abs(100*left*right)就是百倍的精度(即每单位长度显示多少个数值)。那么y坐标又如何表示呢?很简单,y=ax+b,转换成Python语言如下:
y = coefficient_1*x+constant最后上传数据:
plt.plot(x, y)组合+封装(函数)
def linear_function(left, right, coefficient_1, constant):
"""
函数名: linear_function
功能: 显示形如y=ax+b(a≠0)的一次函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
coefficient_1: 一次项系数
constant: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = coefficient_1*x+constant
if coefficient_1 > 0:
if coefficient_1 == 1:
str_cfc1 = "x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
elif constant > 0:
str_cst = "+"+str(constant)
else:
str_cst = str(constant)
else:
if coefficient_1 == -1:
str_cfc1 = "-x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
elif constant > 0:
str_cst = "+"+str(constant)
else:
str_cst = "+"+str(constant)
fig = plt.figure("linear function: y="+str_cfc1 + str_cst, figsize=(10, 8))
fig.canvas.manager.window.wm_geometry('+450+50')
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
plt.show()运行结果:
全部成功!
其它:
其它函数的做法,基本大同小异,整理过的代码如下(EXE下载:Python函数图像工具):
#from posixpath import lexists
import matplotlib.pyplot as plt
import numpy as np
import math
pai = 3.1415926
def linear_function(left, right, coefficient_1, constant):
"""
函数名: linear_function
功能: 显示形如y=ax+b(a≠0)的一次函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
coefficient_1: 一次项系数
constant: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = coefficient_1*x+constant
if coefficient_1 > 0:
if coefficient_1 == 1:
str_cfc1 = "x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
elif constant > 0:
str_cst = "+"+str(constant)
else:
str_cst = str(constant)
else:
if coefficient_1 == -1:
str_cfc1 = "-x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
elif constant > 0:
str_cst = "+"+str(constant)
else:
str_cst = "+"+str(constant)
fig = plt.figure("linear function: y="+str_cfc1 + str_cst, figsize=(10, 8))
print("""
loading function:
type: linear function(y=ax+b, a≠0)
analytic expression: y="""+str_cfc1 + str_cst+"""
state: succeed
""")
fig.canvas.manager.window.wm_geometry('+450+50')
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
def quadratic_function(left, right, coefficient_2, coefficient_1, constant):
"""
函数名: quadratic_function
功能: 显示形如y=ax²+bx+c(a≠0)的二次函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
coefficient_2: 二次项系数
coefficient_1: 一次项系数
constant: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = coefficient_2*(x**2)+coefficient_1*x+constant
if coefficient_2 == 0 and coefficient_1 == 0 and constant == 0:
str_cfc2 = ""
str_cfc1 = ""
str_cst = "0"
elif coefficient_2 == 0 and coefficient_1 != 0:
if coefficient_1 > 0:
str_cfc2 = ""
if coefficient_1 == 1:
str_cfc1 = "x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
else:
str_cst = "+"+str(constant)
else:
str_cfc2 = ""
if coefficient_1 == -1:
str_cfc1 = "-x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
elif constant > 0:
str_cst = "+"+str(constant)
else:
str_cst = str(constant)
else:
if coefficient_2 > 0:
if coefficient_2 == 1:
str_cfc2 = "x²"
else:
str_cfc2 = str(coefficient_2)+"x²"
if coefficient_1 == 1:
str_cfc1 = "+x"
elif coefficient_1 == 0:
str_cfc1 = ""
elif coefficient_1 == -1:
str_cfc1 = "-x"
elif coefficient_1 > 0:
str_cfc1 = "+"+str(coefficient_1)+"x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
elif constant > 0:
str_cst = "+"+str(constant)
else:
str_cst = ""+str(constant)
else:
if coefficient_2 == -1:
str_cfc2 = "-x²"
else:
str_cfc2 = str(coefficient_2)+"x²"
if coefficient_1 == 1:
str_cfc1 = "+x"
elif coefficient_1 == 0:
str_cfc1 = ""
elif coefficient_1 == -1:
str_cfc1 = "-x"
elif coefficient_1 > 0:
str_cfc1 = "+"+str(coefficient_1)+"x"
else:
str_cfc1 = str(coefficient_1)+"x"
if constant == 0:
str_cst = ""
elif constant > 0:
str_cst = "+"+str(constant)
else:
str_cst = ""+str(constant)
fig = plt.figure("quadratic function: y="+str_cfc2 +
str_cfc1+str_cst, figsize=(10, 8))
fig.canvas.manager.window.wm_geometry('+450+50')
print("""
loading function:
type: quadratic function(y=ax²+bx+c, a≠0)
analytic expression: y="""+str_cfc2+str_cfc1+str_cst+"""
state: succeed
""")
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
def exptf(left, right, base_number):
"""
函数名: exptf
功能: 显示形如y=a^x(a>0, 且a≠1)的指数函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
base_number: 底数
"""
x = np.linspace(left, right, abs(100*left*right))
y = base_number**x
fig = plt.figure("exponential function: y=" +
str(base_number)+"^x", figsize=(10, 8))
print("""
loading function:
type: exponential function(y=a^x, a>0, a≠1)
analytic expression: y="""+str(base_number)+"^x"+"""
state: succeed
""")
fig.canvas.manager.window.wm_geometry('+450+50')
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
def logf(left, right, base_number):
"""
函数名: logf
功能: 显示形如y=loga(x)(a>0, 且a≠1)的对数函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
base_number: 底数
"""
x = np.linspace(left, right, abs(100*left*right))
y = np.log(x)/np.log(base_number)
fig = plt.figure("logarithmic function: y=log" +
str(base_number)+"(x)", figsize=(10, 8))
print("""
loading function:
type: logarithmic function(y=loga(x), a>0, a≠1)
analytic expression: y=log"""+str(base_number)+"(x)"+"""
state: succeed
""")
fig.canvas.manager.window.wm_geometry('+450+50')
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
def sinf(left, right, cfc, ivc, phi):
"""
函数名: sinf
功能: 显示形如y=Asin(ωx+φ)(A>0, ω>0)的正弦函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
cfc: 系数
ivc: 自变量系数
phi: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = cfc*np.sin(ivc*x+phi)
if phi == 0 and ivc != 0:
str_phi = ")"
elif phi > 0:
str_phi = "+"+str(phi)+")"
else:
str_phi = str(phi)+")"
if ivc == 1:
str_ivc = "x"
elif ivc == -1:
str_ivc = "-x"
elif ivc == 0:
str_ivc = ""
elif ivc > 0:
str_ivc = str(ivc)+"x"
else:
str_ivc = str(ivc)+"x"
if cfc == 1:
str_cfc = "sin("
elif cfc == -1:
str_cfc = "-sin("
elif cfc == 0:
str_cfc = ""
elif cfc > 0:
str_cfc = str(cfc)+"sin("
else:
str_cfc = "-"+str(cfc)+"sin("
if phi == 0:
str_phi = ")"
if ivc == 0:
str_ivc = ""
str_phi = "0"
if phi == 0 and ivc == 0:
str_ivc = ""
str_phi = "0"
if cfc == 0:
str_phi = "0"
str_ivc = ""
str_cfc = ""
fig = plt.figure("sine function: y="+str_cfc +
str_ivc+str_phi, figsize=(10, 8))
fig.canvas.manager.window.wm_geometry('+450+50')
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
print("""
loading function:
type: sine function(y=Asin(ωx+φ), A>0, ω>0)
analytic expression: y="""+str_cfc+str_ivc+str_phi+"""
state: succeed
""")
def cosf(left, right, cfc, ivc, phi):
"""
函数名: cosf
功能: 显示形如y=Acos(ωx+φ)(A>0, ω>0)的正弦函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
cfc: 系数
ivc: 自变量系数
phi: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = cfc*np.cos(ivc*x+phi)
if phi == 0 and ivc != 0:
str_phi = ")"
elif phi > 0:
str_phi = "+"+str(phi)+")"
else:
str_phi = str(phi)+")"
if ivc == 1:
str_ivc = "x"
elif ivc == -1:
str_ivc = "-x"
elif ivc == 0:
str_ivc = ""
elif ivc > 0:
str_ivc = str(ivc)+"x"
else:
str_ivc = str(ivc)+"x"
if cfc == 1:
str_cfc = "cos("
elif cfc == -1:
str_cfc = "-cos("
elif cfc == 0:
str_cfc = ""
elif cfc > 0:
str_cfc = str(cfc)+"cos("
else:
str_cfc = "-"+str(cfc)+"cos("
if phi == 0:
str_phi = ")"
if ivc == 0:
str_ivc = ""
str_phi = "0"
if phi == 0 and ivc == 0:
str_ivc = ""
str_phi = "0"
if cfc == 0:
str_phi = "0"
str_ivc = ""
str_cfc = ""
fig = plt.figure("cosine function: y="+str_cfc +
str_ivc+str_phi, figsize=(10, 8))
fig.canvas.manager.window.wm_geometry('+450+50')
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
print("""
loading function:
type: cosine function(y=Acos(ωx+φ), A>0, ω>0)
analytic expression: y="""+str_cfc+str_ivc+str_phi+"""
state: succeed
""")
def tanf(left, right, cfc, ivc, phi):
"""
函数名: tanf
功能: 显示形如y=Atan(ωx+φ)(A>0, ω>0)的正切函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
cfc: 系数
ivc: 自变量系数
phi: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = cfc*np.tan(ivc*x+phi)
if phi == 0 and ivc != 0:
str_phi = ")"
elif phi > 0:
str_phi = "+"+str(phi)+")"
else:
str_phi = str(phi)+")"
if ivc == 1:
str_ivc = "x"
elif ivc == -1:
str_ivc = "-x"
elif ivc == 0:
str_ivc = ""
elif ivc > 0:
str_ivc = str(ivc)+"x"
else:
str_ivc = str(ivc)+"x"
if cfc == 1:
str_cfc = "tan("
elif cfc == -1:
str_cfc = "-tan("
elif cfc == 0:
str_cfc = ""
elif cfc > 0:
str_cfc = str(cfc)+"tan("
else:
str_cfc = "-"+str(cfc)+"tan("
if phi == 0:
str_phi = ")"
if ivc == 0:
str_ivc = ""
str_phi = "0"
if phi == 0 and ivc == 0:
str_ivc = ""
str_phi = "0"
if cfc == 0:
str_phi = "0"
str_ivc = ""
str_cfc = ""
fig = plt.figure("tangent function: y="+str_cfc +
str_ivc+str_phi, figsize=(10, 8))
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
fig.canvas.manager.window.wm_geometry('+450+50')
print("""
loading function:
type: tangent function(y=Atan(ωx+φ), A>0, ω>0)
analytic expression: y="""+str_cfc + str_ivc+str_phi+"""
state: succeed
""")
def cotf(left, right, cfc, ivc, phi):
"""
函数名: cotf
功能: 显示形如y=Acot(ωx+φ)(A>0, ω>0)的余切函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
cfc: 系数
ivc: 自变量系数
phi: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = cfc*(pai/2-np.tan(ivc*x+phi))
if phi == 0 and ivc != 0:
str_phi = ")"
elif phi > 0:
str_phi = "+"+str(phi)+")"
else:
str_phi = str(phi)+")"
if ivc == 1:
str_ivc = "x"
elif ivc == -1:
str_ivc = "-x"
elif ivc == 0:
str_ivc = ""
elif ivc > 0:
str_ivc = str(ivc)+"x"
else:
str_ivc = str(ivc)+"x"
if cfc == 1:
str_cfc = "cot("
elif cfc == -1:
str_cfc = "-cot("
elif cfc == 0:
str_cfc = ""
elif cfc > 0:
str_cfc = str(cfc)+"cot("
else:
str_cfc = "-"+str(cfc)+"cot("
if phi == 0:
str_phi = ")"
if ivc == 0:
str_ivc = ""
str_phi = "0"
if phi == 0 and ivc == 0:
str_ivc = ""
str_phi = "0"
if cfc == 0:
str_phi = "0"
str_ivc = ""
str_cfc = ""
fig = plt.figure("cotangent function: y="+str_cfc +
str_ivc+str_phi, figsize=(10, 8))
fig.canvas.manager.window.wm_geometry('+450+50')
print("""
loading function:
type: cotangent function(y=Acot(ωx+φ), A>0, ω>0)
analytic expression: y="""+str_cfc + str_ivc+str_phi+"""
state: succeed
""")
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
def arcsinf(left, right, cfc, ivc, phi):
"""
函数名: arcsinf
功能: 显示形如y=Aarcsin(ωx+φ)(A>0, ω>0)的反正弦函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
cfc: 系数
ivc: 自变量系数
phi: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = cfc*np.arcsin(ivc*x+phi)
if phi == 0 and ivc != 0:
str_phi = ")"
elif phi > 0:
str_phi = "+"+str(phi)+")"
else:
str_phi = str(phi)+")"
if ivc == 1:
str_ivc = "x"
elif ivc == -1:
str_ivc = "-x"
elif ivc == 0:
str_ivc = ""
elif ivc > 0:
str_ivc = str(ivc)+"x"
else:
str_ivc = str(ivc)+"x"
if cfc == 1:
str_cfc = "arcsin("
elif cfc == -1:
str_cfc = "-arcsin("
elif cfc == 0:
str_cfc = ""
elif cfc > 0:
str_cfc = str(cfc)+"arcsin("
else:
str_cfc = "-"+str(cfc)+"arcsin("
if phi == 0:
str_phi = ")"
if ivc == 0:
str_ivc = ""
str_phi = "0"
if phi == 0 and ivc == 0:
str_ivc = ""
str_phi = "0"
if cfc == 0:
str_phi = "0"
str_ivc = ""
str_cfc = ""
fig = plt.figure("arcsine function: y="+str_cfc +
str_ivc+str_phi, figsize=(10, 8))
print("""
loading function:
type: arcsine function(y=Aarcsin(ωx+φ), A>0, ω>0)
analytic expression: y="""+str_cfc + str_ivc+str_phi+"""
state: succeed
""")
fig.canvas.manager.window.wm_geometry('+450+50')
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
def arccosf(left, right, cfc, ivc, phi):
"""
函数名: arccosf
功能: 显示形如y=Aarccos(ωx+φ)(A>0, ω>0)的反余弦函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
cfc: 系数
ivc: 自变量系数
phi: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = cfc*np.arccos(ivc*x+phi)
if phi == 0 and ivc != 0:
str_phi = ")"
elif phi > 0:
str_phi = "+"+str(phi)+")"
else:
str_phi = str(phi)+")"
if ivc == 1:
str_ivc = "x"
elif ivc == -1:
str_ivc = "-x"
elif ivc == 0:
str_ivc = ""
elif ivc > 0:
str_ivc = str(ivc)+"x"
else:
str_ivc = str(ivc)+"x"
if cfc == 1:
str_cfc = "arccos("
elif cfc == -1:
str_cfc = "-arccos("
elif cfc == 0:
str_cfc = ""
elif cfc > 0:
str_cfc = str(cfc)+"arccos("
else:
str_cfc = "-"+str(cfc)+"arccos("
if phi == 0:
str_phi = ")"
if ivc == 0:
str_ivc = ""
str_phi = "0"
if phi == 0 and ivc == 0:
str_ivc = ""
str_phi = "0"
if cfc == 0:
str_phi = "0"
str_ivc = ""
str_cfc = ""
fig = plt.figure("arccosine function: y="+str_cfc +
str_ivc+str_phi, figsize=(10, 8))
print("""
loading function:
type: arccosine function(y=Aarccos(ωx+φ), A>0, ω>0)
analytic expression: y="""+str_cfc + str_ivc+str_phi+"""
state: succeed
""")
fig.canvas.manager.window.wm_geometry('+450+50')
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
def arctanf(left, right, cfc, ivc, phi):
"""
函数名: arctanf
功能: 显示形如y=Aarctan(ωx+φ)(A>0, ω>0)的反正切函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
cfc: 系数
ivc: 自变量系数
phi: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = cfc*np.arctan(ivc*x+phi)
if phi == 0 and ivc != 0:
str_phi = ")"
elif phi > 0:
str_phi = "+"+str(phi)+")"
else:
str_phi = str(phi)+")"
if ivc == 1:
str_ivc = "x"
elif ivc == -1:
str_ivc = "-x"
elif ivc == 0:
str_ivc = ""
elif ivc > 0:
str_ivc = str(ivc)+"x"
else:
str_ivc = str(ivc)+"x"
if cfc == 1:
str_cfc = "arctan("
elif cfc == -1:
str_cfc = "-arctan("
elif cfc == 0:
str_cfc = ""
elif cfc > 0:
str_cfc = str(cfc)+"arctan("
else:
str_cfc = "-"+str(cfc)+"arctan("
if phi == 0:
str_phi = ")"
if ivc == 0:
str_ivc = ""
str_phi = "0"
if phi == 0 and ivc == 0:
str_ivc = ""
str_phi = "0"
if cfc == 0:
str_phi = "0"
str_ivc = ""
str_cfc = ""
fig = plt.figure("arctangent function: y="+str_cfc +
str_ivc+str_phi, figsize=(10, 8))
fig.canvas.manager.window.wm_geometry('+450+50')
print("""
loading function:
type: arctangent function(y=Aarctan(ωx+φ), A>0, ω>0)
analytic expression: y="""+str_cfc + str_ivc+str_phi+"""
state: succeed
""")
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
def arccotf(left, right, cfc, ivc, phi):
"""
函数名: arccotf
功能: 显示形如y=Aarccot(ωx+φ)(A>0, ω>0)的反余弦函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
cfc: 系数
ivc: 自变量系数
phi: 常数项
"""
x = np.linspace(left, right, abs(100*left*right))
y = cfc*(pai/2-np.arctan(ivc*x+phi))
if phi == 0 and ivc != 0:
str_phi = ")"
elif phi > 0:
str_phi = "+"+str(phi)+")"
else:
str_phi = str(phi)+")"
if ivc == 1:
str_ivc = "x"
elif ivc == -1:
str_ivc = "-x"
elif ivc == 0:
str_ivc = ""
elif ivc > 0:
str_ivc = str(ivc)+"x"
else:
str_ivc = str(ivc)+"x"
if cfc == 1:
str_cfc = "arccot("
elif cfc == -1:
str_cfc = "-arccot("
elif cfc == 0:
str_cfc = ""
elif cfc > 0:
str_cfc = str(cfc)+"arccot("
else:
str_cfc = "-"+str(cfc)+"arccot("
if phi == 0:
str_phi = ")"
if ivc == 0:
str_ivc = ""
str_phi = "0"
if phi == 0 and ivc == 0:
str_ivc = ""
str_phi = "0"
if cfc == 0:
str_phi = "0"
str_ivc = ""
str_cfc = ""
fig = plt.figure("arccotangent function: y="+str_cfc +
str_ivc+str_phi, figsize=(10, 8))
fig.canvas.manager.window.wm_geometry('+450+50')
print("""
loading function:
type: arccotangent function(y=Aarccot(ωx+φ), A>0, ω>0)
analytic expression: y="""+str_cfc + str_ivc+str_phi+"""
state: succeed
""")
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
def powf(left, right, index):
"""
函数名: powf
功能: 显示形如y=a^x(a>0, 且a≠1)的指数函数的图像
参数:
left: 显示的区间(下界)
right: 显示的区间(上界)
index: 指数
"""
x = np.linspace(left, right, abs(100*left*right))
y = x**index
t = ""
if index == 1:
t = "y=x"
elif index == 0:
t = "y=0"
else:
t = "y=x^"+str(index)
fig = plt.figure("power function: "+t, figsize=(10, 8))
fig.canvas.manager.window.wm_geometry('+450+50')
print("""
loading function:
type: power function(y=x^a, a>0, a≠1)
analytic expression: """+t+"""
state: succeed
""")
plt.plot(x, y)
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set(xlim=[left, right], ylim=[left, right])
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))
plt.tight_layout()
"""
test data:
1.linear function(linear_function) & quadratic function(quadratic_function)
linear_function(-10, 10, 1, 0)
quadratic_function(-10, 10, 1, 0, 0)
2.exponential function(exptf) & logarithmic function(logf)
exptf(-10, 10, 2)
logf(-10, 10, 2)
3.sine function(sinf) & arcsine function(arcsinf)
sinf(-5, 5, 1, 1, 0)
arcsinf(-5, 5, 1, 1, 0)
4.cosine function(cosf) & arccosine function(arccosf)
cosf(-5, 5, 1, 1, 0)
arccosf(-5, 5, 1, 1, 0)
5.tangent function(tanf) & arctangent function(arctanf)
tanf(-5, 5, 1, 1, 0)
arctanf(-5, 5, 1, 1, 0)
6.cotangent function(cotf) & arccotangent function(arccotf)
cotf(-5, 5, 1, 1, 0)
arccotf(-5, 5, 1, 1, 0)
7.power function(powf)
powf(-10, 10, 2)
"""
print("""
函数信息:
1.linear function(一次函数) -> ln
2.quadratic function(二次函数) -> qdt
3.exponential function(指数函数) -> expt
4.logarithmic function(对数函数) -> log
5.sine function(正弦函数) -> sin
6.arcsine function(反正弦函数) -> arcsin
7.cosine function(余弦函数) -> cos
8.arccosine function(反余弦函数) -> arccos
9.tangent function(正切函数) -> tan
10.arctangent function(反正切函数) -> arctan
11.cotangent function(余切函数) -> cot
12.arccotangent function(反余切函数) -> arccot
13.power function(幂函数) -> pow
""")
try:
key = input("FunctionImagekey\key> ")
if key == "ln":
left = int(input(r"FunctionImagekey\ln\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\ln\right -> 区间(上界)> "))
coefficient_1 = int(
input(r"FunctionImagekey\ln\coefficient_1 -> 一次项系数> "))
constant = int(input(r"FunctionImagekey\ln\constant -> 常数项> "))
linear_function(left, right, coefficient_1, constant)
elif key == "qdt":
left = int(input(r"FunctionImagekey\qdt\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\qdt\right -> 区间(上界)> "))
coefficient_2 = int(
input(r"FunctionImagekey\qdt\coefficient_2 -> 二次项系数> "))
coefficient_1 = int(
input(r"FunctionImagekey\qdt\coefficient_1 -> 一次项系数> "))
constant = int(input(r"FunctionImagekey\qdt\constant -> 常数项> "))
quadratic_function(left, right, coefficient_2, coefficient_1, constant)
elif key == "expt":
left = int(input(r"FunctionImagekey\expt\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\expt\right -> 区间(上界)> "))
base_number = int(input(r"FunctionImagekey\expt\base_number -> 底数> "))
exptf(left, right, base_number)
elif key == "log":
left = int(input(r"FunctionImagekey\log\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\log\right -> 区间(上界)> "))
base_number = int(input(r"FunctionImagekey\log\base_number -> 底数> "))
logf(left, right, base_number)
elif key == "sin":
left = int(input(r"FunctionImagekey\sin\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\sin\right -> 区间(上界)> "))
cfc = int(input(r"FunctionImagekey\sin\cfc -> 系数> "))
ivc = int(input(r"FunctionImagekey\sin\ivc -> 自变量系数> "))
phi = int(input(r"FunctionImagekey\sin\phi -> 常数项> "))
sinf(left, right, cfc, ivc, phi)
elif key == "cos":
left = int(input(r"FunctionImagekey\cos\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\cos\right -> 区间(上界)> "))
cfc = int(input(r"FunctionImagekey\cos\cfc -> 系数> "))
ivc = int(input(r"FunctionImagekey\cos\ivc -> 自变量系数> "))
phi = int(input(r"FunctionImagekey\cos\phi -> 常数项> "))
cosf(left, right, cfc, ivc, phi)
elif key == "tan":
left = int(input(r"FunctionImagekey\tan\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\tan\right -> 区间(上界)> "))
cfc = int(input(r"FunctionImagekey\tan\cfc -> 系数> "))
ivc = int(input(r"FunctionImagekey\tan\ivc -> 自变量系数> "))
phi = int(input(r"FunctionImagekey\tan\phi -> 常数项> "))
tanf(left, right, cfc, ivc, phi)
elif key == "cot":
left = int(input(r"FunctionImagekey\cot\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\cot\right -> 区间(上界)> "))
cfc = int(input(r"FunctionImagekey\cot\cfc -> 系数> "))
ivc = int(input(r"FunctionImagekey\cot\ivc -> 自变量系数> "))
phi = int(input(r"FunctionImagekey\cot\phi -> 常数项> "))
cotf(left, right, cfc, ivc, phi)
elif key == "arcsin":
left = int(input(r"FunctionImagekey\arcsin\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\arcsin\right -> 区间(上界)> "))
cfc = int(input(r"FunctionImagekey\arcsin\cfc -> 系数> "))
ivc = int(input(r"FunctionImagekey\arcsin\ivc -> 自变量系数> "))
phi = int(input(r"FunctionImagekey\arcsin\phi -> 常数项> "))
arcsinf(left, right, cfc, ivc, phi)
elif key == "arccos":
left = int(input(r"FunctionImagekey\arccos\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\arccos\right -> 区间(上界)> "))
cfc = int(input(r"FunctionImagekey\arccos\cfc -> 系数> "))
ivc = int(input(r"FunctionImagekey\arccos\ivc -> 自变量系数> "))
phi = int(input(r"FunctionImagekey\arccos\phi -> 常数项> "))
arccosf(left, right, cfc, ivc, phi)
elif key == "arctan":
left = int(input(r"FunctionImagekey\arctan\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\arctan\right -> 区间(上界)> "))
cfc = int(input(r"FunctionImagekey\arctan\cfc -> 系数> "))
ivc = int(input(r"FunctionImagekey\arctan\ivc -> 自变量系数> "))
phi = int(input(r"FunctionImagekey\arctan\phi -> 常数项> "))
arctanf(left, right, cfc, ivc, phi)
elif key == "arccot":
left = int(input(r"FunctionImagekey\arccot\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\arccot\right -> 区间(上界)> "))
cfc = int(input(r"FunctionImagekey\arccot\cfc -> 系数> "))
ivc = int(input(r"FunctionImagekey\arccot\ivc -> 自变量系数> "))
phi = int(input(r"FunctionImagekey\arccot\phi -> 常数项> "))
arccotf(left, right, cfc, ivc, phi)
elif key == "pow":
left = int(input(r"FunctionImagekey\arccot\left -> 区间(下界)> "))
right = int(input(r"FunctionImagekey\arccot\right -> 区间(上界)> "))
index = int(input(r"FunctionImagekey\arccot\right -> 指数> "))
powf(left, right, index)
else:
print("错误:找不到函数\'"+key+"\',请对照函数信息重新输入。")
plt.show()
except:
print("错误:函数\'"+key+"\'无法运行,请对照函数信息重新输入,注意输入信息均为整数。")