GMM(高斯混合模型)与KMean聚类
最大期望算法EM
EM (Expectation Maximization)算法是一种求参数的极大似然估计方法,可以广泛地应用于处理缺损数据、截尾数据等带有噪声的不完整数据。
- 最大期望算法经过两个步骤交替进行计算:
– 第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;
– 第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
高斯混合模型GMM
GMM(Gaussian Mixture Model)是指该算法由多个高斯模型线性叠加混合而成, 每个高斯模型称之为component。
类似k-means方法,求解方式跟EM一样。
import pandas as pd
data = pd.read_csv('Fremont.csv', index_col='Date', parse_dates=True)
data.head()
import matplotlib.pyplot as plt
%matplotlib inline
data.plot()
data.resample('w').sum().plot() #数据重采样,按周进行计算
data.resample('D').sum().rolling(365).sum().plot()
data.groupby(data.index.time).mean().plot()
plt.xticks(rotation=45)
- pivot表
data.columns = ['West','East']
data['Total'] = data['West'] + data['East']
pivoted = data.pivot_table('Total', index=data.index.time, columns=data.index.date)
pivoted.head()
pivoted.plot(legend=False, alpha=0.01)
plt.xticks(rotation=45)
print(pivoted.shape)
X = pivoted.fillna(0).T.values
X.shape
(24, 1763)
(1763, 24)
from sklearn.decomposition import PCA
X2 = PCA(2).fit_transform(X)
print(X2.shape)
plt.scatter(X2[:,0], X2[:,1])
- GMM
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(2)
gmm.fit(X)
labels = gmm.predict_proba(X)
labels
labels = gmm.predict(X)
print(labels)
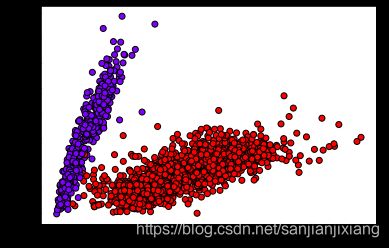
plt.scatter(X2[:,0], X2[:,1], c=labels, cmap='rainbow', edgecolor='k')
array([1, 1, 1, …, 0, 0, 1], dtype=int64)
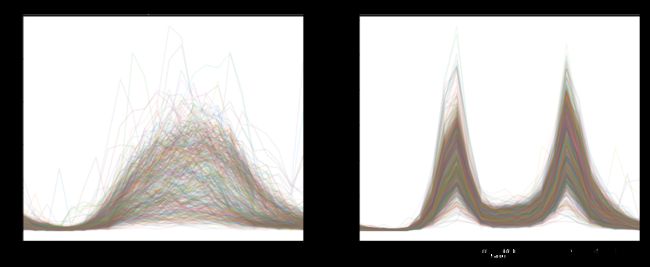
fig,ax = plt.subplots(1, 2, figsize = (16, 6))
pivoted.T[labels == 0].T.plot(legend = False, alpha=0.1, ax=ax[0])
pivoted.T[labels == 1].T.plot(legend = False, alpha=0.1, ax=ax[1])
ax[0].set_title('Purple Cluster')
ax[1].set_title('Red Cluster')
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=800, centers=4, random_state=42)
plt.scatter(X[:,0], X[:,1], c=y_true)
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
plt.scatter(X[:,0], X[:,1], c=y_kmeans, s=50, cmap='rainbow', alpha=0.4)
centers = kmeans.cluster_centers_
plt.scatter(centers[:,0], centers[:,1], marker='*', c='black', s=200)
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=4).fit(X)
labels = gmm.predict(X)
plt.scatter(X[:,0], X[:,1], c=labels, s=40, cmap='summer', edgecolor='k')
import numpy as np
rds = np.random.RandomState(42)
X_stretched = np.dot(X, rds.randn(2,2))
kmeans = KMeans(n_clusters=4, random_state=42)
kmeans.fit(X_stretched)
y_kmeans = kmeans.predict(X_stretched)
plt.scatter(X_stretched[:,0],X_stretched[:,1], c=y_kmeans, s=30, alpha=0.5, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:,0], centers[:,1], c='r', marker='*', s=200)
gmm = GaussianMixture(n_components=4)
gmm.fit(X_stretched)
y_gmm = gmm.predict(X_stretched)
plt.scatter(X_stretched[:,0], X_stretched[:,1], c=y_gmm, s=30, alpha=0.8, edgecolor='k', cmap='autumn')
GMM和K-means对比
最后比较GMM和K-means两个算法的步骤。
GMM:
- 先计算所有数据对每个分模型的响应度
- 根据响应度计算每个分模型的参数
- 迭代
K-means:
- 先计算所有数据对于K个点的距离,取距离最近的点作为自己所属于的类
- 根据上一步的类别划分更新点的位置(点的位置就可以看做是模型参数)
- 迭代
可以看出GMM和K-means还是有很大的相同点的。GMM中数据对高斯分量的响应度就相当于K-means中的距离计算,GMM中的根据响应度计算高斯分量参数就相当于K-means中计算分类点的位置。然后它们都通过不断迭代达到最优。不同的是:GMM模型给出的是每一个观测点由哪个高斯分量生成的概率,而K-means直接给出一个观测点属于哪一类。